Avant-propos

Depuis maintenant dix ans, Atout-Lire travaille en alphabétisation dans le quartier Saint-Sauveur à Québec. À partir des besoins et de la réalité dans notre milieu, des ateliers de calcul ont été mis sur pied en 1986. Actuellement, les personnes qui fréquentent Atout-Lire participent à deux ateliers de calcul par semaine.

Le guide ici présenté est construit sur les bases de notre pratique. Il propose une démarche d'apprentissage des mathématiques, démarche qui concerne de façon spécifique les personnes qui débutent en calcul.

Celles et ceux qui animent des ateliers à ce niveau peuvent y trouver des outils, des exercices et des idées qui serviront à préparer leur travail d'animation. Cependant, il ne s'agit pas d'un modèle "prêt-à-porter"; ce guide suggère plutôt une façon d'aborder les mathématiques, laquelle, il nous semble, doit s'ajuster à la réalité propre de chaque groupe.

En ce sens, le but visé par la rédaction de ce document est bien sûr de fournir des instruments de travail qui pourront alimenter la pratique de formation en calcul, mais de plus, il vise à procurer un cadre global d'animation où chacun et chacune disposent du matériel suggéré en y ajoutant de nouveaux éléments liés à son expérience spécifique.

C'est donc en se rappelant ces éléments que l'on doit aborder le contenu de ce guide.

En vue de mieux situer dans quelles perspectives s'inscrit le guide, on trouvera en introduction quelques précisions concernant le groupe de personnes qui forment l'atelier de calcul, les principes pédagogiques qui sous-tendent l'approche suggérée et une présentation des thèmes choisis et développés dans la démarche.

Quelques préliminaires

Les gens qui commencent un apprentissage en calcul

Dans un premier moment, il apparaît important de présenter brièvement les personnes avec lesquelles nous travaillons. En effet, ces gens montrent des acquis comme des difficultés particulières qu'il importe de reconnaître de façon à concevoir des outils d'apprentissage appropriés.

L'atelier regroupe 12 personnes dont les besoins varient selon la réalité et le cheminement de chacune. Certains points communs sont identifiables entre les participants et participantes mais il existe aussi des écarts dans leur manière d'approcher les notions mathématiques. Le degré d'avancement diffère aussi d'un individu à l'autre, ce qui implique, on le verra, un processus de formation qui doit prendre en compte ces différences.

Les gens ont déjà développé leur propre façon de faire. Il s'agit d'adultes qui possèdent des expériences riches et variées, que l'on a à reconnaître, à apprendre. C'est d'ailleurs à partir de ces expériences, en se basant sur les stratégies de résolution de problèmes déjà utilisées par les personnes, que l'apprentissage des mathématiques peut trouver sa cohérence.

De façon générale, pour ceux et celles qui participent aux ateliers, la valeur de nombres (la numération) pose problème lorsque l'on parle de situations qui ne sont pas directement rattachées au connu ou à des choses pratiques, habituelles. Par exemple, on sait reconnaître la valeur de l'argent; sans grande hésitation, on saura dire combien il reste d'argent dans ses poches si, sur 12$, on en donne 4 à quelqu'un d'autre. Cependant cette même opération, ainsi que le sens de la soustraction, sera plus difficile si la situation choisie comme exemple est abstraite et sans rapport avec le quotidien.

Ceci amène la question du transfert des notions mathématiques apprises. Constamment, les exercices effectués en groupe ou individuellement doivent être appliqués à d'autres situations semblables où les résultats seront les mêmes.

Le transfert des notions n'est pas une démarche spontanée; les personnes n'établissent pas toujours un lien entre l'exercice fait en atelier et une autre situation où l'on retrouve les mêmes données. À ce propos, le questionnement, la discussion, la réflexion, l'illustration concrète et la répétition prennent une place essentielle, déterminante.

La plupart des personnes éprouvent des difficultés à lire et à écrire. En conséquence, les problèmes de calcul doivent être conçus d'une manière simple, où les situations proposées sont imagées et les questions posées oralement.

Les connaissances et la façon d'apprendre n'étant pas uniformes pour toutes les personnes, le contenu des ateliers doit s'ajuster, en partie du moins, aux diverses réalités qui se côtoient dans le groupe. Par exemple, selon les besoins exprimés ou identifiés, une insistance plus forte doit être faite sur la numération pour certains alors que pour d'autres, ces notions étant acquises ou presque, il faut prévoir d'autres types d'exercices correspondant mieux au degré d'avancement.

En somme, il importe d'ajuster constamment les outils utilisés et la démarche proposée selon l'expérience des gens. C'est essentiellement sur des éléments rattachés au connu que se greffent de nouveaux apprentissages qui seront alors porteurs de sens.

L'approche choisie

Certains principes andragogiques encadrent la démarche d'apprentissage proposée. Le guide se développe autour de quelques axes à partir desquels il se structure. Il s'agit, somme toute, de réflexions qui motivent d'une certaine façon notre pratique.

Partir de l'expérience

Les notions mathématiques ont un caractère abstrait; il faut donc ramener les notions à un degré de réalité sensible aux gens. Il devient possible de démystifier les mathématiques en puisant notre matériel d'apprentissage dans le domaine du connu, c'est-à-dire en travaillant à partir de situations que les personnes connaissent parce qu'elles les vivent dans leur quotidien.

Par conséquent, il convient d'exploiter tous les moyens d'apprentissage qui ont une portée concrète, qui sont issus de la vie courante. Ainsi, une personne peut arriver avec un problème auquel elle a été confrontée récemment. Cette situation donnera lieu à une discussion où l'on tentera ensemble de découvrir une ou, plus souvent, des façons de résoudre le problème. De même, les exercices présentés en atelier doivent prendre racine dans l'expérience des gens.

On peut dès lors utiliser des outils simples, peu coûteux, du matériel qui nous entoure, des objets que l'on trouve dans son environnement immédiat (des jetons, de l'argent de papier, des verres servant à illustrer l'unité, la dizaine, la centaine, un dictionnaire pour concrétiser des exercices sur la numération, des jeux de cartes, des circulaires de marchés d'alimentation, etc.). Cela suppose d'être attentif au milieu et aux personnes de façon à saisir toutes les occasions d'apprendre, toutes matières et matériaux, dans la mesure où ils s'inscrivent dans l'univers de l'expérience acquise, où ils permettent de structurer, en langage mathématique, des notions jusqu'à maintenant perçues ou organisées de façon plus intuitive par les personnes.

C'est donc en récupérant des situations familières et/ou en amenant d'autres problèmes rattachés au connu que nous avons voulu orienter le contenu de ce guide.

D'autre part, l'expérience des gens avec qui nous travaillons est vaste. Il existe donc de nombreux thèmes possibles à reprendre dans les ateliers de calcul. Des choix s'imposent. Nous avons voulu prioriser l'essentiel, ce qui peut être utile aux personnes dans leur vie courante, en gardant la préoccupation d'une utilisation immédiate des connaissances acquises.

L'approche que nous adoptons veut tenir compte des priorités fonctionnelles, celles qu'il importe de définir en considérant les besoins ressentis par les personnes dans leurs activités les plus fréquentes. Ces priorités fonctionnelles doivent rejoindre certaines priorités didactiques, en termes d'exigences d'apprentissage (C. Dalbéra, Unesco, 1990).

En fait, les situations et problèmes sans portée pratique ou sans rapport au quotidien sont exclus de la démarche d'apprentissage en calcul qui est mise de l'avant (problèmes abstraits telles les divisions de 3 ou 4 chiffres, les divisions de fractions, la recherche du grand nombre à partir du petit nombre et de la différence ou encore la répétition mécanique des quatre opérations, etc.). Nous voulons plutôt définir un parcours où l'on apprend les mathématiques à partir du connu, d'exemples simples de la vie quotidienne qui peuvent déboucher sur des acquis aussitôt utilisables, qui montrent à la fois un aspect pratique et éducatif.

Nous tentons de nous servir de l'expérience des adultes comme point de départ; par la suite, nous introduisons et explorons les notions mathématiques qui peuvent être intégrées à cette expérience, tout en prenant le temps de reconnaître et de développer le ou les processus de résolution de problème déjà mis en pratique par les personnes.

Nous cherchons ainsi, par divers exercices regroupés autour de thèmes spécifiques en rapport avec le vécu, à ce que les personnes développent les habiletés de base qui leur permettront de régler adéquatement des situations qu'elles peuvent rencontrer dans leur vie courante. L'un des objectifs à moyen et long terme est que la maîtrise de ces habiletés de base soit guidée par une compréhension assez solide pour supporter le transfert des notions à des situations familières et nouvelles.

Comprendre et apprendre

On parle souvent, dans les milieux de l'éducation en général, de l'importance "d'apprendre ". Il nous semble important de préciser notre vision des choses.

"Faire comprendre avant de faire apprendre'' est l'un des principes qui conduit notre approche (selon l'école de "l'enseignement raisonné ", repris dans Beaudry, 1950). Ceci implique entre autres que les personnes participent activement au travail de compréhension de façon à développer leur propre logique et leur façon particulière de raisonner.

Ici la quantité de matières apprises n'est pas la chose la plus importante. On insiste plutôt davantage sur la façon d'enseigner cette matière et la compréhension effective des personnes qui viennent aux ateliers. Nous tentons de placer les adultes dans une situation active d'apprentissage qui leur permettra d'exercer leur jugement, d'identifier, d'approfondir ou de construire graduellement leurs connaissances. On parle ainsi d'apprendre par le jeu du questionnement, du raisonnement, de la logique, de la découverte, jeu qui permet encore plus d'assurer l'acquisition de connaissances durables et transférables.

Par exemple, on laissera les gens composer eux-mêmes des problèmes à partir d'illustrations représentant des regroupements d'objets. Ce faisant, ils ont à travailler leur propre raisonnement, à rechercher des situations (qui appartiennent essentiellement au vécu) où des apprentissages en calcul doivent être mis en pratique. On peut de la sorte mieux comprendre les stratégies des personnes et leur façon d'appréhender certaines notions (addition, soustraction, etc.). Les différences individuelles sont à considérer, on doit s'y ajuster et personnaliser le travail d'animation en fonction de ces écarts inévitables entre les personnes, écarts qui se montrent par ailleurs riches en possibilités d'apprentissage pour tout le monde. On échange des trucs et la façon de faire des certaines personnes peut en aider d'autres à mieux comprendre.

Dans toute la démarche entreprise, on cherche à développer la compréhension de mécanismes ou de principes mathématiques qui mènent à une ou plusieurs solutions à un problème, et non pas à cultiver le réflexe d'une répétition mécanique de chiffres, de nombres ou d'opérations. Le cheminement effectué vise à susciter une réflexion conduisant à découvrir, par soi-même, à quel moment l'on doit recourir à l'une ou l'autre des notions mathématiques connues. Dans cet optique, travailler à partir d'exemples tirés de la vie quotidienne permet aux personnes, en plus d'exploiter leur capacité logique, de participer activement à résoudre certains problèmes, de collaborer intellectuellement à leur apprentissage. Elles sont concernées parce qu'interpellées par la situation en tant que telle et par la façon de la régler.

Nous travaillons en vue de mettre en place un processus qui devrait mener les personnes à "apprendre à apprendre ", c'est-à dire à pouvoir identifier leur façon de résoudre des problèmes. Le travail de compréhension est un prérequis pour atteindre cet objectif. Il faut prendre le temps nécessaire pour y arriver; il s'agit là d'une démarche à long terme, laquelle ne peut être subordonnée aux impératifs d'une quantité de matière à apprendre dans un laps de temps donné.

Nous rejoignons Beaudry quand il affirme que la résolution de tout problème passe par quatre étapes inévitables que l'on doit bien identifier:

• comprendre les valeurs numériques (ce qui se rattache à la numération);
• voir quelles relations unissent les quantités en cause;
• connaître le rôle, le sens, la portée et les effets des diverses opérations;
• finalement, et en dernier lieu seulement, connaître les techniques de calcul.

On essaie ainsi de développer une manière d'apprendre qui part des applications pour aller ensuite vers le calcul exact, les techniques. De là l'importance de la participation active des personnes à toutes ces étapes de l'apprentissage et de s'ajuster à leur rythme.

Le concret, la manipulation

On l'a déjà précisé, il importe de sortir les mathématiques de l'abstraction dans laquelle elles baignent en travaillant avec du matériel concret, dont la manipulation est facile et qui fait référence à ce que les personnes connaissent (exemples: pour comprendre ce qu'est un kilo par rapport à une livre, on pèse des produits dont les poids diffèrent; pour mieux voir la valeur d'un nombre, on reconstitue le nombre en faisant des regroupements d'objets divers, etc.).

Partant du concret et du semi-concret, on vise, par une démarche à long terme, à développer la compréhension qui va mener à appliquer ce qui est appris à d'autres situations, ce qui exige une certaine capacité d'abstraction.

Le travail sur les opérations mathématiques n'est pas détaché du contexte de leur utilisation. On tente d'introduire une notion mathématique par le biais d'une situation qui demande qu'on y ait recours: en comparant, par exemple, les prix de deux produits alimentaires identiques, quel est le moins cher, comment on peut faire pour savoir c'est quoi la différence de prix entre les deux? On essaie ainsi de trouver des situations concrètes où la soustraction est nécessaire pour résoudre un problème.

C'est aussi en cherchant dans l'expérience de vie des personnes qui participent aux ateliers de calcul que l'on trouve en grande partie le matériel d'apprentissage. De plus, puisque les situations soulevées font référence au connu, les personnes peuvent éventuellement mieux reconnaître (explorer ou encore développer) leur propre stratégie de résolution de problème.

On choisit ainsi des situations-problèmes simples à partir desquelles on tente de dégager certaines règles et principes mathématiques; les applications demeurent pratiques. Parce que les personnes arrivent à s'imaginer facilement la situation, cela tend à réduire ou à atténuer le caractère plus abstrait de certaines notions. Ainsi, les tables de multiplication ont une portée plus concrète si, par exemple, on associe la table de 7 aux 7 jours de la semaine, si la table de 12 est liée aux mois de l'année ou à des douzaines d'œufs, ou encore si l'on comprend dans quels cas la multiplication peut être utile (comment fait-on pour savoir le salaire gagné dans une journée de 8 heures, à $5/h?).

La répétition, il faut le rappeler, joue un rôle essentiel: avec du matériel différent, des situations diverses, on peut reprendre un même problème ou une même situation mathématique en tentant d'identifier les obstacles auxquels se heurtent les personnes et les causes de ces obstacles à l'apprentissage.

Il faut chercher à ce que les personnes créent peu à peu leur "expérience mathématique'' par une démarche où l'on fait des essais, où l'on utilise ses erreurs pour apprendre, où l'on constate qu'il peut y avoir plusieurs solutions pour un même problème et plusieurs problèmes pour une même solution.

Enfin, le concret, l'illustration et la manipulation sont d'autant plus importants lorsque l'on considère la difficulté de lecture des personnes. Cette difficulté, ajoutée à celle causée par le langage mathématique, en raison de son abstraction et de sa rigueur, rend l'apprentissage plus ardu. Il importe donc de vulgariser tant le vocabulaire que l'écriture ou la notation mathématique, de les démystifier. On doit voir entre autres à ce que les mots n'aient qu'un sens, et le même pour tout le monde. Les termes utilisés doivent être simplifiés (ex. la soustraction est un moins: on enlève, on ôte, on retire, on diminue, ...). D'autre part, on verra le sens des différentes opérations, ou l'idée, avant de présenter le signe (la représentation symbolique). On apprendra donc à se familiariser avec la phrase mathématique en travaillant auparavant sur un problème pour trouver la solution; une fois discutés et compris le sens et la solution du problème, on cherchera la façon décrire ce problème en langage mathématique.

Les thèmes abordés

Les thèmes abordés (et comment y intégrer les notions)

Le guide est divisé en quatre modules. Chacun présente un thème particulier à travers lequel on peut explorer différentes notions. Les thèmes proposés sont:

1. la numération
2. l'argent et le budget
3. le groupe d'achat (poids et mesures)
4. le temps

Le choix de ces thèmes est motivé tant en raison des besoins et intérêts identifiés chez les personnes que par leur caractère familier, pratique, qui favorise des apprentissages basés sur l'expérience. Par exemple, le thème du temps ouvre une multitude de possibilités: en observant le calendrier et en considérant les mois ou le passage des années, on peut apprendre la régularité des nombres; en calculant le nombre d'heures travaillées en fonction d'un salaire horaire, on peut introduire l'addition et la multiplication; en voyant le nombre de jours dans la semaine, on peut étudier la table de 7; en travaillant la demi-heure et le quart d'heure, on fait l'apprentissage des fractions simples, etc.

Les notions mathématiques de base prévues à ce niveau d'apprentissage se retrouvent donc à l'intérieur de chaque module. Nous avons voulu développer une approche globale, en quelque sorte décloisonner l'apprentissage, de façon à faire prendre conscience que les mathématiques sont un outil qui sert à régler de différentes façons des situations diverses. En conséquence, on ne trouvera pas dans ce guide une partie spécifique à l'addition ou encore à la soustraction, etc.

Il arrive souvent qu'un problème en amène un autre ou fasse surgir un questionnement qui, la plupart du temps, permet d'élargir à de nouveaux apprentissages, d'intégrer de nouvelles connaissances. En effet, chaque situation peut être développée par des questions propices qui servent à ouvrir le champ des apprentissages, à découvrir de nouvelles notions. Souvent aussi, telle notion est liée à telle autre, s'y enchaîne ou la complète. Par exemple, en comparant des sacs de sucre de 2 et 4 kilos, on peut choisir de travailler en premier lieu sur les poids différents, mais il est possible d'y intégrer la notion de demie, celle de volume (contenant/contenu), de multiplication et de division (le prix d'une quantité par rapport à l'autre), etc.

C'est en ce sens que chaque module reprend les mêmes notions qui sont ainsi revues, répétées et retravaillées de multiples manières, ce qui peut, entre autres, favoriser le transfert des notions d'une situation à une autre et l'établissement de liens avec le connu ou la vie courante des personnes.

Ceci n'élimine pas l'importance d'une progression cohérente. Ainsi, la connaissance de la valeur des nombres et des exercices sur la numération constitue le premier module puisque ces connaissances sont la base d'autres apprentissages en calcul.

Toutefois, il convient de signaler que progression "cohérente" ne signifie pas "linéaire ". La plupart du temps, les notions ne sont pas abordées isolément, par cases individuelles qui ne se toucheraient pas, mais elles servent à en intégrer d'autres ou, à tout le moins, à ouvrir la porte à de nouveaux apprentissages éventuels. Plutôt qu'une progression linéaire ou un apprentissage par notions séparées sans liens entre elles, ce qui risque de réduire (ou détruire) le sens global de ce que l'on fait par absence de relations, il est possible d'opter pour un cheminement où les apprentissages s'inscrivent dans une structure organisée (tel un casse-tête) où les notions s'emboîtent les unes dans les autres, se complètent, où l'on apprend par un processus essais/erreurs.

On peut illustrer ceci par un problème posé en atelier: la comparaison entre deux produits de 65¢ et 63¢. Les personnes savaient spontanément que l'écart est 2c. Mais pour arriver à la façon mathématique de trouver cette différence, il a fallu prendre le temps d'essayer les différentes solutions envisagées par les personnes. Elles ont d'abord songé à la division, puis à la multiplication et ensuite à la soustraction de 65-2, pour finalement découvrir la solution 65-63. Pendant tout le travail de recherche pour arriver à résoudre le problème, on a questionné chaque solution mise de l'avant pour comprendre le sens précis de chaque opération proposée, pour savoir à quoi chacune peut servir.

Cette manière d'apprendre dégage de plus un espace pour prendre en compte les différents degrés d'avancement entre les personnes qui composent le groupe et s'y ajuster. Par exemple, alors que des personnes travaillent à comparer des prix pour trouver la différence, d'autres peuvent très bien trouver le prix unitaire d'un produit à partir du prix fixé pour une plus grande quantité.

Ainsi, considérant l'approche choisie, on retrouve, en plus des objectifs spécifiques contenus dans chaque module, un ensemble d'objectifs généraux applicables à toutes les étapes de la démarche de formation présentée dans ce guide:

• connaître la valeur et l'ordre des nombres;
• savoir lire et écrire les nombres;
• se familiariser et comprendre le langage ainsi que l'écriture - la notation - mathématiques (le sens, les signes, le vocabulaire) dans les cas de:
  - l'addition,
  - la soustraction,
  - la multiplication,
  - la division;
• apprendre à faire les quatre opérations de base;
• savoir lire et écrire les montants d'argent;
• comprendre les fractions simples (1/2, 1/4);
• développer le questionnement, le raisonnement, le jugement critique;
• reconnaître et approfondir ses stratégies de résolution de problèmes;
• apprendre à observer, à classer et à reconnaître les données pertinentes pour résoudre un problème.

De plus, à l'intérieur des exercices compris dans ces modules, on apprendra à utiliser la calculatrice comme outil pouvant supporter l'apprentissage de certaines personnes qui ont plus de difficultés à mémoriser. Un usage approprié de la calculatrice implique nécessairement que l'on connaisse bien le sens de chaque opération, les signes propres au langage mathématique, l'écriture des nombres de même que les situations où l'emploi de la calculatrice est pertinent. Ces derniers éléments revêtent, à notre avis, plus d'importance que la seule capacité de procéder mécaniquement aux techniques de calcul exact, laquelle ne fait pas essentiellement référence à la compréhension, au sens mathématique.

En somme, ce qui importe en premier lieu, c'est que les personnes arrivent à développer une façon d'aborder les mathématiques en utilisant leur capacité de réflexion et de jugement, qu'elles voient les mathématiques comme un outil qui peut les aider à comprendre et régler des situations qui leur causent problème.

C'est en cela que l'on tente d'aller davantage vers une approche de résolution de problème parce qu'elle nous semble plus formatrice que de se limiter à l'acquisition d'habiletés ou d'automatismes en calcul, lesquels, par manque de souplesse et de compréhension, risquent d'être difficilement applicables aux situations variées de la vie.

Il faut bien se rendre compte également que les besoins de chaque personne sont différents; les apprentissages à faire et les acquis à développer ne peuvent être les mêmes pour tous et toutes.

En conséquence, nous proposons une démarche de formation en calcul axée sur des apprentissages fonctionnels, qui vise à prendre le plus possible la réalité des participantes et participants comme matériau de travail. Dans cet optique, il nous importe de saisir toutes les occasions pertinentes qui permettent l'approfondissement de certaines notions ou l'initiation à de nouvelles.

Nous tentons, au fil du processus, de faire ressortir les relations entre les concepts développés pour que puisse surgir un sens global des mathématiques, sans lequel l'apprentissage tend à perdre toute sa valeur et sa portée pratique.

L'observation, la manipulation, la verbalisation, comme la réflexion critique et le raisonnement, font partie intégrante du processus mis de l'avant. Nous essayons de susciter la participation active des gens à la résolution de problème et au travail de compréhension de façon à ce qu'ils construisent eux-mêmes leur propre expérience mathématique. Le but visé est que les personnes acquièrent, à leur rythme, des connaissances transférables à des situations éventuellement différentes.

Enfin, il importe de reconnaître les mécanismes qu'ont déjà acquis les personnes pour régler certaines situations-problèmes dans leur vie courante. Ces façons de faire, en plus d'aider à comprendre le fonctionnement respectif des gens et les obstacles auxquels ils se confrontent parfois, jouent souvent un rôle déterminant dans l'intégration de nouvelles connaissances à celles déjà acquises.

En fait, nous espérons pouvoir rendre effectives les conditions d'un apprentissage signifiant.

Module 1 – Le temps

Temps: nom, masc. (lat. tempus ) Grandeur caractérisant à la fois la durée des phénomènes et les instants successifs de leur déroulement. // Durée limitée par rapport à l'usage qu'on en fait: bien employer son temps. // Moment favorable, occasion: il y a un temps pour tout. //

[Voir l'image pleine grandeur]

La plupart des personnes qui participent aux ateliers de calcul sont en mesure de définir le temps à partir des divisions déjà connues tels l'année, le mois, la semaine, le jour ou l'heure. Cependant les relations à établir entre ces différentes unités ou catégories de temps n'apparaissent pas toujours claires. C'est ainsi que des difficultés surgissent lorsque l'on désire soit évaluer des périodes de temps, soit connaître l'année de naissance dune personne proche, soit se situer dans le temps, etc.

Ces problèmes peuvent être liés à un manque de compréhension de la structure temporelle (la division du temps, la durée, etc.) mais aussi de certaines notions mathématiques de base telles la lecture, l'écriture ou la valeur des nombres et le sens des opérations mathématiques, de même qu'à une difficulté d'abstraction.

L'expérience que nous avons vécue nous fait croire qu'il est tout à fait possible de débuter la démarche en abordant la question du temps. En effet, tout au cours de l'expérimentation auprès du groupe, nous avons découvert de nombreuses possibilités de développement d'exercices rattachées à cette thématique. Celle-ci permet de présenter diverses notions de base en calcul. On peut en effet initier certains concepts tout en traitant de sujets qui se rapportent à des situations concrètes, ancrées dans le quotidien des gens, et qui, souvent, leur créent des problèmes.

Pour beaucoup, nous avons travaillé à partir de jeux, d'exercices de manipulation et d'observation, d'activités simples qui suscitent la réflexion, le raisonnement. Nous avions en outre la préoccupation constante d'utiliser du matériel peu coûteux et accessible.

Ce module constitue ainsi un "bloc" spécifique où l'on explore diverses notions qui seront revues et approfondies dans les autres modules (la numération, l'argent et le budget et le groupe d'achat).

Objectif général

Sensibiliser à la notion de temps: comprendre la notion de temps et de durée, bien définir et préciser le temps.

Objectifs spécifiques

1. Se situer dans le temps
2. Lire le calendrier
3. Lire et écrire les dates
4. Lire et écrire l'heure
5. Comprendre le système à l'échelle de 12 et 24 hres
6. Calculer les périodes de temps

Notions mathématiques contenues dans ces apprentissages
L'initiation au langage mathématique
La valeur des nombres
L'initiation aux 4 opérations
La pratique des 4 opérations
L'initiation aux fractions

Nous avons profité du changement d'année, du passage de l'année 1992 à 1993 pour introduire le thème du temps. Ainsi, l'année 93 est une nouvelle année mais c'est aussi la succession, l'addition des toutes les années passées et il suffit d'ajouter quelques années seulement pour arriver à l'an 2000. Nous allons utiliser cette situation pour présenter et comprendre diverses notions mathématiques.

1. Se situer dans le temps

Objectif spécifique
Se situer dans le temps

Exercice
Sensibilisation aux divisions du temps

Matériel
Un dictionnaire par personne ou un annuaire de téléphone de Montréal

Fonctionnement
En grand groupe

Notions mathématiques contenues dans ces apprentissages
Valeur et ordre des nombres
Lecture des nombres
Compter par 1, par 10, par 100, par 1000
Initiation à l'addition et à la soustraction
Initiation à la moitié ou demie

Démarche

Nous avons demandé à une personne d'écrire la nouvelle date au tableau, puis nous avons posé une série de questions pour connaître la perception qu'ont les personnes du temps et des grands nombres: D'où vient ce chiffre 1993? Pourquoi 1993 et pas 193?

Y a-t-il déjà eu une année 998? une année 100? une année 1000? Étiez-vous nés en 980? Votre père était-il né? votre grand-père?

Il a été assez surprenant de voir toute la confusion qui est apparue à la suite de ces questions. Ainsi à la question étiez-vous nés en 980, les gens répondent oui. Cette méprise vient d'un manque de perception de la relation entre le cummul des ans dans le temps et l'ordre des nombres.

Travail avec le dictionnaire

Pour bien faire comprendre et illustrer le temps et les années, nous avons utilisé le dictionnaire. Chaque personne devait avoir le sien.

Imaginons que chaque page illustre une année écoulée depuis la naissance du Christ ou le début de notre ère. Toutes les pages (épaisseur) représentent environ 2000 ans. (Il a fallu faire un petit cours d'Histoire.)

Séparons de visu le dictionnaire en deux parties à peu près égales (la moitié) pour illustrer deux fois mille ans (millénaires). Est-ce qu'on vit dans le premier mille ans ou le deuxième?

Chercher la page mille (quelle année vient avant 1000? laquelle vient après? ) et continuer à tourner les pages pour constituer un siècle (100 pages représentent 100 ans).

À l'œil, selon l'épaisseur, faisons des siècles jusqu'à 1900. Compter par 100, de 1000 à 1900. Puis cherchons notre année de naissance en comptant par 10: 1900, 1910, 1920, 1930, 1940... et comparer les années vécues (âge) avec un siècle, avec mille ans (par l'épaisseur des pages toujours).

Ensuite pour travailler l'ordre des nombres et leur relation avec le temps, nous avons cherché la date d'événements ou de découvertes importantes (voir annexe).

Une activité amusante, pour compléter celle du dictionnaire, est de trouver l'âge qu'on aura en l'an 2000. Une personne écrit au tableau 1993 et les années qui suivent, jusqu'à l'an 2000.

Sous 1993, elle écrit son âge, puis celui qu'elle aura pour chaque année correspondante (ex.: en 1993, Marie aura 48 ans.):

1993	1994	1995	1996	1997	1998	1999	2000
48	49	50	51	52	53	54	55

Devinette: en l'an 2000, j'aurai 46 ans, quel est mon âge actuel?

Ces activités permettent:

• d'expliquer et de visualiser les millénaires, les siècles et les décennies;
• de situer des événements importants, des dates historiques et des grandes découvertes;
• de comprendre les termes avant et après;
• de mieux comprendre la suite des nombres;
• de se familiariser avec les grands nombres.

Remarques:

• Manipuler les pages du dictionnaire est un moyen concret pour les personnes de se représenter la valeur du nombre (par exemple, la valeur de 100 par rapport à 1000).
• En empilant les dictionnaires, on peut illustrer et compter des mille et imaginer ce que peut être le million.

Difficultés rencontrées / Solutions essayées

• Le dictionnaire n'a pas 2000 pages:
• Il faudra le préciser et situer où il s'arrête dans le temps, ou alors trouver un livre plus épais, l'annuaire de Montréal par exemple.
• On confond 991 et 1991. À la question: est-ce que Tannée 991 est passée, on répond oui, mais si on formule la même question avec l'année 998, on répond non:
• Pour transférer la connaissance acquise de la valeur de l'argent à celle des grands nombres et des années, on pose le problème ainsi:
  si je te fais un chèque de 998$ et un autre de 1998$, lequel choisirais-tu? Pourquoi?
  998$ est proche de quoi? De 1000$.
  1998$ est proche de quoi? De 2000$.
  Est-ce la même chose avec les années? avec les pages du dictionnaire? avec le nombre de personnes dans une manifestation? avec les chiffres 998 et 1998?
• Les personnes ont de la difficulté à chercher une page-année dans le dictionnaire. Elles sont portées à tourner une page à la fois, ce qui est long si, par exemple, on va de 1000 à 1500.
• Faire évaluer des épaisseurs de 100 pages puis compter: 1000, 1100, 1200, 1300...

2. Lire le calendrier

Objectif spécifique
Lire le calendrier

Exercice
Travail sur le calendrier

Matériel
Des calendriers, le globe terrestre une illustration du système solaire

Fonctionnement
En grand groupe

Notions mathématiques contenues dans ces apprentissages
Valeur et ordre des nombres
Initiation à l'addition
Initiation à la multiplication: compter par 3, par 7, par 12
Initiation à la division: combien de 7 jours dans 14, 21, 28
Initiation à la demie

Démarche

Démarche discussion préalable
Comment mesure-t-on le temps? D'où viennent ces divisions du temps (année, mois, jour)?

Nous avons expliqué avec une illustration du système solaire et le globe terrestre d'où viennent ces divisions du temps: le jour et la nuit, les saisons, et l'année terrestre.

Nous avons aussi expliqué l'histoire du calendrier grégorien (voir feuilles en annexe).

Travailler avec et sur le calendrier
Chaque personne a son calendrier de l'année représenté sur une seule feuille. (Il serait aussi possible de faire son propre calendrier)

Les exercices qui suivent permettent de lire et d'écrire le nom des mois ou à tout le moins de les reconnaître visuellement. Combien de mois dans une année? Les nommer.

À côté de chaque mois, écrire le chiffre qui y correspond pour en faciliter la lecture (01, 02, 03, 04, etc.).

Quel mois vient	avant le mois de septembre, de décembre, de février?
	après le mois de mars, de juillet, d'octobre?
Quel est	le 8e mois, le 3e mois, le 11e mois, etc.?
Trouve les mois	qui ont 31 jours;
	le mois le plus court;
	les mois qui se suivent qui ont 31 jours;
	les mois qui ont 30 jours.

En travaillant avec le calendrier, nous avons abordé certaines notions telles l'addition, la multiplication et la division.

Combien de mois dans:	1 an, 2 ans, 3 ans, 4 ans?
	12 + 12 + 12 + 12
2 fois 12 mois,	ça fait combien de mois?
3 fois 12 mois,	ça fait combien de mois?
4 fois 12 mois,	ça fait combien de mois?

Combien de 12 mois dans: 24 mois; 36 mois; 48 mois?

La fille de Stéphane a 15 mois.
Peux-tu le dire autrement?
A-t-elle plus qu'un an?
Y a-t-il plus que 12 mois dans 15 mois? Combien de mois de plus?
Coller deux calendriers côte à côte et calculer.
Dans 15 mois, il y a 12 mois et 3 autres mois. Peu importe à quel mois on commence à calculer, 12 mois égalent toujours un an.
Mon fils a 1 an et demi. Donne son âge en mois.
Comment faire pour le trouver? (Voir difficultés.)

Difficultés rencontrées / Solutions essayées

• Combien de mois dans 2 ans, 3 ans, 4 ans?
• Pour transférer la connaissance acquise de la multiplication 2 fois 12, on pose le problème sous une autre forme: si tu achètes 2 caisses de 12 bières (douzaines d'œufs), tu auras combien de bières (d'œufs)?
  Si tu cherches combien il faut de mois pour faire 2 ans, que dois-tu faire?
  1 an, c'est 12 mois + 1 an, un autre 12 mois soit 2 fois 12 mois.
  2 groupes de 12, ça fait toujours 24.
  2 fois 12 heures, 2 fois 12$, 2 fois 12 personnes égalent toujours 24.
• Combien d'années dans 24 mois, 36 mois, 48 mois?
• On peut introduire aussi la notion de division. Combien de caisses vides me faut-il pour placer 12, 24, 36. 48 œufs?
  Combien de 12 mois (calendriers) dans 24, dans 36, dans 48 mois?
  Si tu as 24 mois pour payer ton nouveau frigidaire, ça te prendra combien d'années à rembourser? Si tu commences en mars 93, quand feras-tu ton dernier paiement?
• La fille de Stéphane a 15 mois. Peux-tu donner son âge en ans et en mois? Ceci est une autre forme de la division. Ce problème introduit la division avec reste.
• La fille de Stéphane a-t-elle plus qu'un an? Oui. Si elle avait un an, elle aurait combien de mois? Elle a donc 12 mois plus combien de mois? Avec ses doigts, on complète 13, 14, 15, ce qui donne 1 an et 3 mois. Dans 15 mois, j'ai une fois 12 mois et il reste 3 mois. On peut aussi compter les mois sur le calendrier.
• Pour introduire la notion de fraction, on peut poser ce problème:
  mon fils a 1 an et demi; peux-tu donner son âge en mois?
• Que veut dire 1 an et demi?
  Cela veut dire que mon fils a 1 an plus 1/2 année.
  Si mon fils avait seulement 1 an, il aurait combien de mois? 12.
  Il a donc 12 mois plus 1/2 année.
  
  Que veut dire 1/2? C'est la même chose que la moitié.
  C'est donc la moitié d'un an ou de 12 mois.
  Quelle est la moitié de 12?
  C'est comme une boîte d'œufs, 6 d'un côté, 6 de l'autre.
  La demie ou la moitié, c'est la même chose.
  12 mois plus la demie de 12 mois (6 mois) font 18 mois.
  Trouve la demie de 12$, de 12 personnes, de 12 heures?
  
  Peux-tu trouver la demie de 4, de 6, de 8, de 10, de 14, etc.

Exercices complémentaires

Compter par 2, par 10 et par 12.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Compter par 3, par 12 et par 15.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Calcule le nombre de bouteilles.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Situons les semaines

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Compter par 7.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Situons les jours

Quel jour tombera:	ta fête cette année?
	le jour de Noël?
	la St-Jean-Baptiste?
	le 2e mercredi de juin, etc.?
* Le 4e dimanche du mois d'octobre sera quelle date?

Quel jour sera-t-il dans 5 jours? dans 7 jours? dans 14 jours?

Quelle opération mathématique peut être faite pour arriver à la même réponse? Par exemple, si on est le 17, 5 jours plus tard, on sera le 22:
[17 + 5-22].

Il y a 5 jours, 7 jours, 14 jours, on était quelle date?

Quelle opération mathématique peut être faite pour arriver à la même réponse?
[17 - 5 = 12]

JEU: Je me promène dans le mois de mars

Objectif
Initier à l'addition et à la soustraction en utilisant la connaissance du calendrier et le vocabulaire mathématique:
ajouter, enlever, plus, moins, avancer, reculer (de plus, de moins), etc.

Utiliser un mois de l'année comme base du jeu.
Point de départ: le premier mercredi de mars, ajouter 7 jours, revenir en arrière de 3 jours, plus 4 jours, moins 6 jours, avancer de 5 jours, retourner une semaine en arrière, aller au prochain jeudi. Où êtes-vous rendus? quelle date, quel jour?

Chercher combien de jours dans une année?
Plusieurs stratégies sont possibles:

1. Compter les jours un à un (démarche longue et difficile);
2. Additionner les jours de chaque mois;
3. Multiplier 52 semaines par 7 + 1 jour.(difficile à expliquer)

Certaines personnes ont essayé de compter tous les jours du calendrier. Cependant cet exercice s'est avéré long et mêlant et personne ne s'est rendu à la fin du calcul. D'autres ont suggéré plutôt d'additionner les jours de chaque mois. Ainsi la recherche du nombre de jours dans une année devient un exercice de calcul. De plus faire l'exercice au tableau comme ci-dessous permet d'apprendre à compter par 3.

On cherche le nombre de jours dans 1 an

[Voir l'image pleine grandeur]

Ces activités permettent:

• d'effectuer divers regroupements des nombres (par 1, par 3, par 7, par 12);
• de prendre conscience de la valeur des nombres;
• d'établir un lien entre la valeur des nombres et la durée du temps;
• de comprendre l'organisation du temps (passage des jours aux semaines, des semaines aux mois, des mois à l'année).

Remarques:

• On portera une attention particulière aux dates inscrites en double dans une case du calendrier à la fin de certains mois (23/30 ou 24/31).
• Situer le jour qui suit la fin d'un mois (si le mois se termine un dimanche, le jour suivant est un lundi).
• Faire prendre conscience que la dernière semaine du mois est incomplète et qu'elle s'achève avec la première semaine du mois suivant pour faire 7 jours.
• Situer le premier jour de l'année suivante. Pour bien visualiser, compléter la dernière semaine de décembre en faisant écrire les jours qui suivent (ex: 29 30 31 1 2 3) dans les espaces libres. Faire la distinction entre le premier jour de la semaine et le premier jour du mois.
• Souligner la différence entre la semaine complète de 7 jours et la semaine de cinq jours de travail.
• Faire remarquer la différence entre l'expression "dans 15 jours" et le nombre de jours dans 2 semaines.

Autres exercices complémentaires

Calcule

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercices de pratique

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

3. Lire et écrire les dates

Objectif spécifique 3
Lire et écrire les dates

Exercice
Travail sur la carte d'assurance maladie et le calendrier

Matériel
Cartes d'assurance maladie, formulaires, calendrier

Fonctionnement
En grand groupe

Notions mathématiques contenues dans ces apprentissages
Lecture des nombres
Notions d'addition et de soustraction

Démarche

La carte d'assurance-maladie
Chaque personne doit avoir sa carte d'assurance-maladie. On observe les chiffres et on explique à quoi ils correspondent.

Le numéro:	les lettres et les chiffres représentent le
	nom et la date de naissance (pour les
	femmes on ajoute 50 au mois de
	naissance; faire le calcul pour vérifier).
La date de naissance:	l'année (les 2 derniers chiffres), le mois et le jour
La date d'expiration:	vérifier la date (et parler de la photo à
	faire prendre pour la prochaine carte).

• Découvrir la façon d'écrire la date (l'année, le mois, le jour). Pourquoi écrit-on seulement les 2 derniers chiffres de l'année de naissance? (40 02 14)
• Quelle âge aurait une personne née en 1900? en 1899?
• Sur certains formulaires, on peut aussi écrire: le jour, le mois et l'année. Il faut bien faire la distinction.

Jeu

• Mêler les cartes d'assurance-maladie puis les distribuer.
• La première personne qui joue donne la date de naissance seulement, par exemple, 40 06 23.
• La personne qui reconnaît sa date de naissance reprend sa carte et donne à son tour la date de naissance inscrite sur la carte qu'elle a en sa possession.
• Si une carte n'est pas réclamée, on la place à l'envers au centre de la table.
• Quand tous les joueurs et joueuses ont repris leur carte, on retrouve la ou les personnes qui n'ont pas récupéré leur carte. Pour cela, elles doivent aller écrire au tableau leur date de naissance.

Exercices complémentaires

• Trouver l'âge des personnes à partir de leur date de naissance ou, le contraire, trouver l'année de naissance à partir de leur âge.
• Écrire la date du jour.
• Écrire sa date de naissance.
• Découvrir le jour indiqué:
  01-01-93
  24-06-93
  93-12-24

Signer et dater le formulaire de la commission scolaire ou tout autre formulaire disponible.

Ces activités permettent:

• de se familiariser avec sa carte d'assurance-maladie (savoir les informations qu'elle contient);
• de mieux comprendre les formulaires que les personnes doivent compléter;
• de pouvoir calculer les périodes de temps écoulées depuis certains événements;
• de reconnaître son année de naissance.

Lire et écrire l'heure

Objectif spécifique 4
Lire et écrire l'heure

Exercice
Lecture du cadran

Matériel
Un cadran avec chiffres et aiguilles, un cadran numérique, des illustrations d'une horloge sur carton, avec aiguilles et minutes indiquées, un chronomètre

Fonctionnement
En grand groupe

Notions mathématiques contenues dans ces apprentissages
Initiation à l'addition
Compter par 5, par 10, par 15, par 20.
Initiation aux fractions (la demie et le quart)

Démarche

Avec un cadran, faire lire l'heure indiquée.

Chaque personne indique une heure sur son cadran, les autres peuvent la reproduire sur leur horloge de carton. On donne l'heure à tour de rôle.

Dire autrement:

• 3 h moins 20
• 9:45 h
• 4 h moins 10
• 3:55 h etc.

Pourquoi dit-on 3 h moins 20? Faire calculer, avec le cadran, combien il manque de minutes pour faire 3 heures.

Pourquoi dit-on 9:45 h? Faire calculer les minutes qui se sont écoulées de 9:00 h à 9:45 h. Compter les minutes par 5.

Écrire l'heure indiquée sur le cadran de son voisin.

L'heure

[Voir l'image pleine grandeur]

Partir de l'intérêt pour introduire des notions:

L'observation du cadran numérique et du chronomètre a occasionné une discussion sur les sports que l'on voit à la télé. Est-ce que ce sont des minutes ou des secondes qui s'écoulent à la fin du jeu (hockey, ski, courses, etc.)? Sans s'attarder sur les fractions de seconde, nous avons quand même expliqué les dixièmes de seconde comme étant une division du temps en parties très petites, une fraction de l'unité.

L'échange se faisant surtout autour du hockey, nous avons profité du sujet pour travailler la lecture du cadran en simulant le jeu.

Explication du jeu:
Le groupe est divisé en 2 équipes.
On définit 3 périodes de jeu de 20 minutes.
Calculer sur le cadran combien font 3 périodes de 20 minutes.
Revenir sur l'opération en introduisant le vocabulaire mathématique: 3 fois 20 minutes égalent 60 minutes ou 20 + 20 + 20 = 60

• Imaginer des situations de jeu (arrêts, hors jeu, buts, punitions, etc.). Chaque équipe marque le temps sur son cadran et donne l'heure indiquée.
• Exemple: la partie commence à 7:30 h, on indique l'heure sur nos cadrans. Après 8 minutes de jeu, un premier point est compté. Quelle heure est-il? L'indiquer sur le cadran. Cinq minutes plus tard, un joueur a une punition. Quelle heure est-il? L'indiquer sur le cadran. Expliquer sa stratégie.
• Exemples d'autres questions à poser pendant le jeu:
  la punition est de 2 minutes, quand peut-il revenir au jeu?
  combien de temps reste-t-il avant la fin de la période?
  combien de temps s'est-il écoulé depuis le début de la période? etc.
• On donne un point par bonne réponse (c'est-à-dire la bonne heure indiquée sur le cadran) et un point supplémentaire si on peut expliquer sa méthode de calcul.

Difficultés rencontrées / Solutions essayées

• Distinguer les heures et les minutes sur le cadran. On est souvent porté à lire les minutes de la même façon que les heures. Par exemple, on dira 8:7 au lieu de 8:35.
• Il faut bien faire voir que les chiffres inscrits sur le cadran correspondent aux chiffres des heures. Puis faire inscrire par chaque personne, sur son cadran en carton, les minutes correspondant aux petites lignes entre chaque chiffre pour indiquer ainsi les minutes. Marquer de cette façon les 60 minutes comprises dans l'heure en faisant calculer par 5.
• Lire l'heure à partir de la deuxième demi-heure, c'est-à-dire 8 h moins 20, 7 h moins 10, etc. et faire la différence entre 8 h et 20, 7 h et 10.
• Poser la question suivante: à 8 h moins 20, est-ce que 8 h est passé? Non, combien manque-t-il de minutes avant 8 h? Il manque 20 minutes avant d'arriver à 8 h. On dit donc qu'il est 8 h moins 20 (8 h moins 20 minutes). À 8 h et 10, est-ce qu'on a dépassé 8 h? Il est 8 h plus 10 minutes; on dit alors qu'il est 8 h et 10. À l'aide de divers exemples, on peut reprendre ces questions.
• La notation de l'heure; par exemple, on écrit 8:5 pour 8:05 h.
• Pour visualiser la manière d'écrire l'heure, on utilise un cadran numérique. (Il est aussi possible d'utiliser l'horaire télé, tout en faisant un exercice de lecture.)
• Comparer les heures: 8 h moins 25 et 8:35 h. etc.
• On calcule par 5 les minutes sur le cadran en portant une attention particulière à partir de 30 minutes. Les personnes doivent établir la correspondance entre [35 et -251, entre [40 et -20] etc. Comment peut-on dire autrement 2 h moins quart, 10 h moins 10? etc. Travailler avec les cadrans de carton pour que les personnes, en plaçant les aiguilles, voient bien les heures et les minutes.
• Calculer les minutes et faire la distinction avec les heures: le chiffre marquant l'heure est pris comme base de calcul pour les minutes.
• Reprendre le cadran et refaire calculer les minutes entre les chiffres indiqués. On peut utiliser un gros cadran pour observer l'aiguille des minutes. Répéter les exercices et souligner qu'en calculant les minutes, ce sont des tranches de 5 minutes que l'on calcule entre chaque chiffre écrit sur le cadran.
• Faire le passage d'une heure à l'autre, par exemple, de 1:59 h à 2:00 h.
• Jouer avec le cadran en plaçant les aiguilles de façon à devoir lire l'heure: de 2:25 à 3:00 h, de 3:56 à 4:10 h en comptant par 1 (une minute), puis par 5, etc.
  Exemple: 2:26 h, 27, 28, 29, 30, 35, 40, 45, 50, 55, 60 = 3:00 h

Initiation à la demie et au quart

Matériel
Des illustrations du cadran sur un carton (utiliser des couleurs différentes)
Mêmes représentations du cadran, avec des couleurs autres, mais cette fois en parties découpées:

• en deux (30 minutes)
• en trois (20 minutes)
• en quatre (15 minutes)
• en six ( 10 minutes)
• en douze (5 minutes)

Pour bien visualiser les fractions représentées par les parties de cadran, il convient de reproduire ce dernier sur un carton de couleur et de découper les morceaux qui illustrent la demie, le quart, les 20 minutes (tiers), les 10 minutes (sixièmes) et les 5 minutes (douzièmes). Utiliser des couleurs contrastantes.

Déroulement:

Distribuer à chaque groupe de deux personnes une illustration du cadran entier, puis les morceaux d'un autre cadran découpé.

Chaque groupe doit reconstituer le cadran et dire ce que les morceaux représentent en fractions (pour la demie et le quart seulement) et en minutes pour les autres morceaux. On parlera d'un morceau sur trois pour les 20 minutes, d'un morceau sur six pour les 10 minutes et d'un morceau sur 12 pour les 5 minutes.

Questions:

• Pourquoi dit-on 1 heure et demie au lieu de 1:30 h?
  D'où vient la demie, c'est la demie de quoi?
• Quel terme est aussi utilisé pour dire la demie? La moitié.
  Qu'est-ce qu'on fait pour trouver la demie?
  Que fait une demie plus une demie?
  Combien y a-t-il de demies dans une heure?
  J'ai 2 demi-heures et j'enlève une demie. Que reste-t-il?
  Comment s'écrit une demie en chiffre?
• En s'aidant avec les parties découpées de cadran:
  trouver la demie dune heure;
  trouver la demie de 60 minutes;
  trouver la demie de 30 minutes.
• Pourquoi dit-on 1 heure et quart?
• D'où vient le quart, c'est le quart de quoi?
  Qu'est-ce qu'on fait pour trouver le quart?
  Que fait un quart plus un quart? plus un autre quart?
  Combien y a-t-il de quarts dans une heure? Si j'enlève un quart, que reste-t-il? Si j'enlève 2 quarts? ou 3 quarts, que reste-t-il?
  Comment s'écrit un quart en chiffre?
• Montrer le morceau qui représente le quart d'une heure.
  Trouver le quart de 60 minutes.
  Trouver les trois quarts dune heure.
  Combien y a-t-il de quarts d'heure dans une demi-heure?
  Comment s'écrit trois quarts en chiffre?
• Comparer les autres morceaux avec les demies et les quarts.
• Combien faut-il de morceaux pour cacher le cadran?
• Quel morceau est le plus gros, le plus petit?
• Peux-tu les placer en ordre, du plus grand au plus petit?
• Dire ce que chaque forme représente en minutes.
• Combien de morceaux de 5 minutes y a-t-il dans une heure, dans une demi-heure, dans un quart d'heure?
• Combien de morceaux de 10 minutes y a-t-il dans une heure, dans une demi-heure?
• Combien de morceaux de 20 minutes y a-t-il dans une heure, dans une demi-heure? etc.

5. Comprendre le système à l'échelle de 12 et 24 heures

Objectif spécifique 5
Comprendre le système à l'échelle de 12 et 24 heures

Exercice
Faire l'horaire de sa journée

Matériel
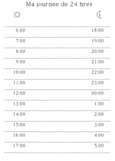
Feuille "Ma journée de 24 heures''

Fonctionnement
Individuellement

Notions mathématiques contenues dans ces apprentissages
Initiation à l'addition et à la multiplication

Démarche

Discussion sur les activités dans sa journée et présentation de la feuille "Ma journée de 24 heures".

Observons la façon dont sont indiquées les heures.

À quel moment commence la journée (à 00:00 h, à 6 h)?
À quel moment commence-t-on à compter les heures de la journée?
Que représente 00:00 h?
Que signifient le soleil et la lune sur la feuille?

Comment pourrait-on dire autrement 22 h?
Vois-tu un lien entre 6 h et 18 h?
Compter les heures de 6 h à 18 h.
Est-ce la même chose entre 3 h et 15 h ou entre 5 h et 17 h?

Compter les heures dans la journée.
Combien de 12 heures y a-t-il?
Peux-tu expliquer pourquoi on dit 13 h au lieu de 1 h?

Exercice

Indiquer sur sa feuille "Ma journée de 24 heures" les actions suivantes:

• l'heure qui indique le début d'une nouvelle journée
• l'heure à laquelle tu te lèves
• l'heure des repas
• l'heure de l'émission "Le hockey des Nordiques"
• l'heure à laquelle tu te couches
• ton horaire de cours etc.

Problème surprenant

Ce problème à opérations multiples est surprenant quant au résultat et amène les gens à réfléchir sur l'importance de leur présence aux ateliers, sur le temps (la durée) que représente les 2000 heures de formation (règlement de l'aide sociale et du ministère). Il permet aussi de travailler le sens des opérations à partir des notions du temps.

Calculer le temps passé en ateliers pour une période de 32 semaines.

Calculer combien de jours par année représentent ces heures de cours si on plaçait les heures bout à bout.

Il faut d'abord calculer le temps pour une semaine.
Puis pour 32 semaines.
Enfin convertir ces heures en jours.

Le calcul des heures représente la première difficulté: 1 hre à 4 hres ne représente pas 4 mais bien 3 heures. La deuxième difficulté réside dans le calcul des heures pour 32 semaines à 15 heures /semaine.

Si dans 1 semaine je fais 15 heures.
dans 2 semaines je fais 15+15 hres ou 2 fois 15 heures.
dans 3 semaines je fais 15 + 15 + 15 heures ou 3 fois 15 heures.

ainsi de suite pour avoir un tableau semblable

15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres,
15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres,
15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres,
15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres, 15 hres,

Les gens qui ne comprennent pas le sens, l'effet de la multiplication essaieront d'additionner tous ces chiffres. La calcul peut se faire en ligne, en colonne, par tranche de 10 et de 5. C'est une bonne pratique.

Cependant si on veut montrer l'avantage de la multiplication, il faut amener le raisonnement du sens de l'opération 32 fois 15 hres.

Le calcul peut se faire avec la calculatrice car la multiplication à deux chiffres n'a pas encore été abordée

J'ai ensuite 480 heures à transformer en jours.

De la même façon, il faut amener le raisonnement qui exprime le sens de la division.

24 hres font 1 jr
48 hres font 2 jrs
72 hres font 3 jrs de 24 hres

À l'aide de la calculatrice, certains participants ont continué ainsi jusqu'à 480 pour trouver 20 jours.

Pour amener l'idée de la division, c'est à dire, combien j'ai de 24 hres dans 480 heures, il faut travailler avec des petits chiffres: combien j'ai de 5c dans 25c? Les gens savent qu'il faut séparer le 25¢ en 5¢. Ainsi avec les heures, il faut séparer les 480 hres en groupes de 24 hres. Séparer veut dire la même chose que diviser, ce qui demande une division comme opération.

Il est trop difficile à cette étape d'expliquer la division à deux chiffres, la calculatrice devient donc l'outil qui permet de résoudre l'opération.

Il est évident que ce problème s'adresse aux plus avancés du groupe, mais tout le monde a pu quand même apprendre à travers ce travail de recherche.

Ma journée de 24 heures

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Calculer les périodes de temps (et le salaire)

Objectif spécifique 6
Calculer les périodes de temps (et le salaire)

Exercices
a) La course à relais
b) Mises en situation

Matériel
a) Une règle et une craie de tableau
b) Feuilles-illustrations de cadrans

Fonctionnement
a) En grand groupe
b) Individuellement

Notions mathématiques contenues dans ces apprentissages
Addition et soustraction Initiation à la division

Jeu - La course à relais

On demande à un participant ou à une participante de prendre le témoin (règle) et d'aller écrire son nom et sa date de naissance au tableau, puis de revenir porter la règle à son voisin. Celui-ci doit à son tour aller écrire son nom et sa date de naissance et ainsi de suite, jusqu'à ce que toutes les personnes aient passé.

Pendant ce temps, les autres joueurs et joueuses comptent, à "voix basse", les secondes écoulées: 1 -2-3-4-5 etc. Si on en a un chronomètre, on pourra l'utiliser.

On écrit le résultat sur une feuille où l'on aura d'abord inscrit le nom de tous les joueurs et joueuses, dans l'ordre.

Combien de temps a-t-on pris pour faire la course?
Il faudra faire le total des secondes.
Nombre de secondes
Combien cela fait-il de minutes?
Combien faut-il de secondes pour faire une minute?
Est-ce que j'ai plus de 60 secondes?

Il faut trouver combien de 60 secondes sont comprises dans le total.

Est-ce que j'ai un 60 dans le total? Est-ce que j'en ai plus qu'un? Combien environ?

Voici des solutions proposées par le groupe:

• en soustrayant les 60 secondes contenues dans le total,
  exemple: 248 sec. - 60 sec. = 188 - 60 sec. = 128 - 60 sec. = 68 - 60 sec. = 8 sec,
• en calculant: 2 fois 60 donnent 120 secondes que j'enlève à 248, il reste 128 secondes. J'ai encore 2 fois 60 que j'enlève aussi et il me reste 8 secondes.

Avec les personnes plus avancées, on demandera de trouver la moyenne de temps pris par le groupe. On se servira de l'exemple des sports pour introduire cette notion (au hockey, au baseball ou au patinage artistique).:

Si on enlève les 2 temps les plus courts et les 2 temps les plus longs, on aura déjà une bonne idée de la moyenne: 28 s - 42 s - 54 s - 35 s- 22s -37 s - 39 s -36 s

Mises en situation

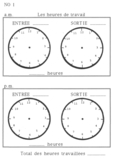
No 1 Calculer les heures de travail

Mon voisin m'engage à l'occasion pour faire de la peinture. Je dois calculer mes heures de travail pour être payé. Hier, j'ai travaillé de 9 heures à midi et de 1 heure à 5 heures. Combien d'heures j'ai travaillé dans ma journée?

Indiquer les heures dans le cadre de la page suivante:
entrée et sortie dans l'avant-midi, entrée et sortie dans l'après-midi.
Expliquer le sens de a.m. et p.m. au-dessus du cadre.
En utilisant les cadrans, calculer toutes les heures travaillées.

Mon voisin me donne $5 de l'heure, quel sera mon salaire? (Toute une discussion peut se faire à partir de cette situation sur le droit au travail, sur le salaire minimum et l'aide sociale, sur la place et le travail des personnes immigrantes, etc.)

L'expression $5 de l'heure ou "taux horaire'' doit être expliqué avant tout puisque c'est dans la compréhension de cette expression que se trouve la solution. L'expression sous-entend en fait $5 pour chaque heure travaillée.
1 hre 1 hre 1 hre 1 hre 1 hre 1 hre 1 hre
5 + 5 + 5 + 5 + 5 + 5 + 5

Calculer le salaire à des taux horaires différents permet d introduire les tables ou le calcul par... On commence d'abord à $5 et à $10 de l'heure car c'est plus facile. Puis on reprend les tables déjà vues soit $7 ou $12 de l'heure.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Calculer les heures de gardiennage au no 2.

Une participante calculait les heures de sa gardienne en comptant l'heure du début. Ainsi, elle payait 1 heure de plus en comptant de 6 hres à 10 hres: 6, 7, 8, 9,10, soit 5 heures.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

No 3 Calculer les minutes de la pause.

Inscrire sur les cadrans l'heure du début de la pause. Puis au retour, indiquer l'heure de la fin de la pause. Calculer les minutes qu'a duré la pause.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Autres problèmes:

Tu appelles au Centre pour parler à ton animatrice. Elle est occupée et on te demande de rappeler dans une demi-heure. Si tu as appelé à 9 heures et quart, à quelle heure dois-tu rappeler?

Il faut 45 minutes pour cuire un gâteau. Tu mets ton gâteau au four à 2 hres moins 20. À quelle heure sera-t-il prêt?

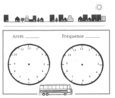
L'horaire d'autobus

Faire son horaire d'autobus à partir de sa situation.

Pour aller à Atout-Lire, ça me prend 5 minutes à pied pour me rendre à l'arrêt d'autobus, et 15 minutes de trajet en autobus. L'autobus passe aux 15 minutes et l'atelier commence à 6:30h, à quelle heure dois-je partir de chez moi?

L'autobus passe aux 15 minutes. Il arrive devant chez moi à 6:10 h Prévois l'heure pour le prochain autobus.

Le soir, l'autobus passe aux demi-heures. S'il est passé à 8:40 h, à quelle heure sera le prochain autobus?

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Commentaires généraux pour conclure

Nous avons choisi ce thème en raison des problèmes identifiés chez les participants et participantes à ce propos. Par exemple, certains avaient de la difficulté à définir à quelle heure ils devaient partir de chez eux pour aller à tel rendez-vous; d'autres cherchaient à connaître l'année de naissance de leur mère ou à comprendre ce que signifiait vraiment 8 h moins 10, etc. La notion de durée, parce que très abstraite, n'avait pas ou peu de référence dans l'esprit des gens, la division du temps en secondes, minutes, heures ou en jours, semaines, mois, années étant confuse pour plusieurs. La classification chronologique d'événements posait aussi des difficultés, etc.

Les personnes, par les connaissances liées à leur vécu, possédaient bien sûr "l'intuition" du temps: elles savaient reconnaître les repères temporels, identifier les éléments spécifiques à leur expérience, etc. C'est davantage sur le plan des rapports à établir entre ces données, en quelque sorte la vision globale de la structure temporelle et la prise de conscience de ce que contient le temps, que des obstacles surgissaient.

Toutes les composantes du "temps", pour être bien maîtrisées, exigent des connaissances minimales de l'écriture des nombres et du système de numération, dont entre autres la valeur des nombres. Pour être intégrées, elles requièrent également la compréhension du sens de certaines opérations mathématiques et de certains termes (avant, après, plus, moins, etc.), comme de la notion de groupement.

Dans les faits, la question du temps a permis de voir les notions mathématiques sous un autre angle, dans une autre perspective.

Comme il a été mentionné précédemment, la thématique du temps a ouvert un champ d'apprentissage global en calcul, et cela au-delà de ce que nous avions prévu au départ.

Nous nous sommes rendu compte, en cours de route, à quel point ce module constituait un moyen riche pour prendre contact et se familiariser avec le monde des mathématiques et, à la fois, pour introduire de nombreuses notions de base. Les exercices ont souvent contribué à déceler des difficultés chez les personnes. En ce sens, ce travail sur le temps pose en partie les balises de la démarche à venir en établissant des liens avec le contenu des autres modules: les notions introduites à cette étape-ci seront reprises plus loin où elles seront approfondies, développées davantage et mises en rapport avec d'autres.

L'expérimentation s'est étalée sur plusieurs semaines. Beaucoup de place a été faite aux exercices de manipulation ou d'observation et aux jeux. À cette étape de l'apprentissage, nous avons priorisé ce type d'activités qui permet de découvrir par soi-même, à son rythme, tout en donnant accès graduellement aux notions à aborder. De plus, il s'agissait d'insister davantage sur la verbalisation, le questionnement et la réflexion.

Ce module a permis d'initier les personnes au langage mathématique, au vocabulaire employé plus qu'aux signes, bien que nous ayons saisi les moments opportuns qui survenaient pour présenter des symboles ou la notation mathématiques. Par exemple, en observant le calendrier, on a pratiqué la lecture et l'écriture des nombres et observé la suite des nombres; mais de plus, le mois de février et ses 4 semaines de 7 jours pouvaient donner lieu à l'apprentissage de l'addition (7 + 7 + 7 +7) et à l'introduction de la multiplication (4 X 7).

Ou encore le travail sur les demi-heures et les quarts d'heures a mis en place les données servant à l'introduction des fractions simples. Certaines personnes ont d'ailleurs relié cette connaissance à d'autres cas semblables: on a fait le lien avec une demie ou un quart de livre de steak haché, une demie tasse de sucre, etc. Ceci constituait notamment des notions qui seraient revues plus loin dans la partie "groupe d'achat".

De plus, puisque le temps est un thème qui permet de travailler à partir de diverses situations quotidiennes, il est arrivé régulièrement que des périodes, en début d'atelier, ont été utilisées pour tenter de résoudre les problèmes individuels que des gens amenaient. Par exemple, trouver l'année de naissance d'un parent ou ami à partir de son âge (initiation à la soustraction), trouver le salaire gagné par un participant à partir du tarif/horaire et du nombre d'heures travaillées (initiation à l'addition et à la multiplication), etc. Ces types de problèmes, parce qu'ils avaient une portée très concrète, favorisaient la compréhension et permettaient l'acquisition de connaissances. Ainsi, le contenu des ateliers a été ajusté de façon constante aux situations nouvelles que les personnes voulaient discuter.

D'autre part, nous estimons que l'utilisation du dictionnaire comme outil de formation en calcul donne des résultats positifs. Il rend "palpable" le passage du temps et permet de visualiser ce que contient un nombre. En manipulant et fouillant dans le dictionnaire, on peut mieux percevoir que 1000, par exemple, contient en lui-même les nombres précédents: on prend conscience qu'avant la page 1000, il y a 10 tranches de 100 pages. Déjà, la notion de groupement (et la multiplication) peut être abordée et prendre forme lentement.

La démarche effectuée rend compte de difficultés spécifiques rencontrées par les gens. Lune d'entre elle réside dans la notion de durée. Par exemple, reculer dans le temps, se reporter des années en arrière, arriver à concevoir de longues périodes de temps, situer le présent par rapport au passé posaient problème. On doit arriver à créer des images mentales qui peuvent contrer l'abstraction évidente de cette notion. La visualisation et la manipulation à l'aide du dictionnaire, la répétition de diverses situations semblables qui exigent une même façon de régler le problème soulevé sont des moyens que nous avons utilisés. La juste perception du temps peut aussi s'affermir en travaillant sur la division du temps à partir de repères déjà connus, sur des ensembles déjà constitués (7 jours dans une semaine, 12 mois dans une année, 100 années dans un siècle, etc.) et en interrogeant les situations familières (Ton père est-il né avant ou après toi? Était-il né en l'an 200, en 1800, en 1894? etc.). En somme, il s agit là d'un travail à moyen et à long terme où la compréhension de la valeur réelle des nombres prend une place déterminante.

En fait, on doit tenter de développer la capacité d'abstraction chez les personnes avec qui nous travaillons de manière à rendre possible le transfert des notions apprises. Il nous faut développer des moyens qui permettent de partir du connu pour le dépasser et élargir les connaissances. C'est ainsi qu'un participant n'arrivait pas à résoudre la mise en situation suivante: le temps requis pour partir de chez toi et te rendre chez le médecin est de 30 minutes, à quelle heure arriveras-tu chez le médecin si tu pars de chez toi à 2:15 h? La personne ne pouvait trouver la réponse car, en réalité, ça lui prend 5 minutes à pied pour aller chez son médecin.

Il nous faut donc avoir constamment en tête cette réalité. Ce n'est pas parce que l'on s'inspire de situations concrètes que le transfert des notions se fait nécessairement, automatiquement. C'est un processus long et complexe. Et il n'y a pas de solutions "miracles". La capacité de transférer des notions est essentiellement liée à la capacité d'abstraction. En conséquence, il convient de tenir compte de ces préoccupations dans la façon d'aborder le contenu des ateliers et les activités d'apprentissage.

Finalement, la notation de l'heure et l'écriture des dates sont des éléments sur lesquels on a dû revenir fréquemment. Les gens n'étaient pas familiers avec cette façon d'écrire. Par exemple, l'écriture des dates impliquent que l'on puisse numéroter les mois, donc savoir les compter sur un calendrier. Cela n'est pas toujours évident car la consultation du calendrier n'est pas vraiment un geste coutumier pour les personnes. Dans un premier temps, l'attention a été portée sur le décodage: que signifient les chiffres indiquées et l'ordre dans lequel ils se trouvent? On a ensuite effectué la transcription de diverses heures et dates: écrire l'heure du début de l'atelier, l'heure de son émission préférée, la date du jour, celle de son anniversaire, etc. Se pratiquer à lire et écrire les heures et les dates s'est montré le moyen le plus efficace pour que les personnes s'habituent à ces formes de notation. Cependant, il nous fallait revenir régulièrement sur ces notions. C'est ainsi que fréquemment, en début d'atelier, on demandait d'écrire sur une feuille la date du jour. Souvent des erreurs se glissaient. Dans la plupart des cas, on fait face à un problème de mémorisation, problème qui l'on rencontre tout au cours du processus d'apprentissage.

Somme toute, les participants et participantes ont apprécié les activités de ce module. Nous pensons que cette démarche rencontre les objectifs d'apprentissage fixés au départ. Certains exercices devront sans doute être améliorés et, selon le cas, adaptés aux multiples situations et réalités que vivent les personnes composant les groupes.

Annexes

1. Quelle date sommes-nous?

[Voir l'image pleine grandeur]

2. C'est génial!

-4000	Apparition de l'écriture en Mésopotamie (aujourd'hui l'Irak)
-2780	Établissement du calendrier de 365 jours par les prêtres égyptiens
-1500	Domestication du chat en Égypte, où il est vénéré et momifié
800	Invention de l'école par Charlemagne
1434	Invention de la presse à imprimer par Gutenberg
1450	Invention des lunettes pour les myopes
1453	Publication de la théorie de Copernic selon laquelle la Terre est ronde et tourne autour du Soleil. Beaucoup ne le croient pas.
1570	Invention de la brosse à dents
1762	Invention du sandwich par le cuisinier de John Montagu, comte de Sandwich 1778 Invention des toilettes à eau courante 1818 Première transfusion de sang, à Londres
1826	Invention de la boîte de conserve, en Angleterre. L'ouvre-boîte n'est pas encore inventé!
1829	Invention du braille par Louis Braille, aveugle depuis l'âge de trois ans. Son alphabet est adopté par tous les pays du monde en 1932.
1860	Louis Pasteur découvre le principe de la pasteurisation qui permet de conserver le lait et d'autres aliments.
1862	Invention du patin à glace
1867	Invention de la dynamite par Alfred Nobel
1876	Invention du téléphone par Alexander Graham Bell
1878	Invention de l'ampoule électrique par Thomas Edison
1880	Invention du patin à roulettes
1884	Popularisation de la poubelle sur l'ordre du chef de police Eugène Poubelle
1886	Invention de l'automobile à pétrole

3. Inventions

1892	Apparition du Coca-Cola en Amérique
1893	Invention de l'aspirine par le chimiste Adolf von Bayer
1895	Invention du pneu par les frères Michelin Invention du cinéma par les frères Lumière
1896	Découverte de la radio
1897	Lancement sur le marché des "Corn Flakes" par les frères Kellogg
1903	Fabrication du premier avion
1914	Apparition des premiers feux de circulation
1922	Invention du réfrigérateur
1924	Invention des mouchoirs de papier
1926	Avènement du cinéma pariant
1936	Invention de la télévision
1940	Invention du stylo à bille Invention du magnétophone
1942	Découverte de l'énergie nucléaire
1945	Invention de la bombe atomique
1946	Invention de l'ordinateur
1947	Invention des verres de contact
1948	Invention du four à micro-ondes 1954 Premières greffes d'organes
1957	Lancement du premier satellite artificiel
1960	Découverte du rayon laser
1969	Conquête de la Lune Apparition de la télévision en couleurs
1978	Naissance du premier bébé-éprouvette

(Tiré de: Textes et contextes)

4. Quelle heure est-il?

Le cadran solaire date de 3000 ans avant notre ère. C'est l'horloge la plus ancienne.

[Voir l'image pleine grandeur]

La montre à eau (ou clepsydre) mesure le temps à partir de la quantité d'eau s'écoulant d'un vase. On l'utilisait en Égypte, en Grèce et à Rome en 1500 avant notre ère.

[Voir l'image pleine grandeur]

Le sablier date de 1250 de notre ère. On l'utilise encore pour minuter la cuisson des œufs à la coque.

[Voir l'image pleine grandeur]

La première "horloge portative" apparaît en Italie vers 1400. Avant, l'heure n'était indiquée que sur les édifices et les monuments publics.

[Voir l'image pleine grandeur]

En 1904, Louis Cartier crée une montre-bracelet pour l'aviateur Santos-Dumont. Les soldats de la Première Guerre mondiale en ont répandu l'usage. Il a aussi été dit que la première montre aurait été fabriquée il y a 500 ans...

[Voir l'image pleine grandeur]

On sait depuis 1929 que le cristal de quartz permet une très grande précision. Mais la première montre au quartz n'apparaît qu'en 1970.

[Voir l'image pleine grandeur]

(Tiré de: Je me petit débrouille septembre 1989)

Module 2 – La numération

Numération: nom. Fém. Façon d'écrire les nombres (numération écrite ) et de les énoncer (numération parlée ).

[Voir l'image pleine grandeur]

Nombre, numération et dénombrement
Une clé indispensable

Les principes et les caractéristiques (valeur positionnelle et additive) de notre système de numération à base 10, avec ses unités, ses dizaines et ses centaines, sont les fondements de l'univers des mathématiques. L'enseignement de ces notions est à la base de la compréhension de la valeur des nombres entiers et décimaux, des mécanismes des opérations tels la retenue et l'emprunt, du principe et de la technique de la multiplication, enfin de la compréhension de tous les calculs à venir car ils se fondent en grande partie sur le mécanisme de ce système de numération.

Lorsqu'on est attentif aux difficultés rencontrées par les participantes et les participants, on établit vite le lien entre ces difficultés et la mauvaise connaissance de ce système. En fait, les personnes qui participent aux ateliers de calcul, ne saisissent pas toutes le concept du nombre. C'est-à-dire qu'elles savent en général réciter sans trop se tromper la suite des nombres, mais cette activité est parfois mécanique. De plus, plusieurs personnes sont aussi confrontées avec le problème de l'écriture et de la lecture des nombres dû à une méconnaissance de la valeur positionnelle de ceux-ci. Enfin, les principes de la numération et les relations à établir entre ce système et les algorithmes de calcul n'apparaissent pas du tout clairs et sont à la source de ces difficultés.

En conséquence, il apparaissait indispensable de consacrer, au début de la "session", une période de temps assez longue pour permettre aux gens de découvrir ce système et d'organiser ces éléments dans un ensemble cohérent.

Dans le but d'apprivoiser ces notions abstraites, il fallait les présenter par le biais d'une approche concrète et visuelle. Pour ce faire, il a fallu trouver des situations où les gens auraient à manipuler, à regrouper et à compter des objets en se servant de la base 10. Les pages qui suivent expliquent la méthode utilisée pour introduire ces notions. Le matériel employé est simple, peu coûteux, facile à utiliser et facilement remplaçable. En l'expérimentant dans les ateliers, on découvrira toute la richesse et les possibilités de ces outils (des verres en plastique, des dictionnaires, etc.).

Objectif général
Découvrir et comprendre les principes de notre système de numération.

Objectifs spécifiques

1. Apprendre le regroupement par 10
2. Lire et écrire les nombres
3. Découvrir la régularité dans les nombres
4. Comprendre la valeur positionnelle et additive
5. Initier à la multiplication

Notions mathématiques contenues dans ces apprentissages
Le langage et les symboles mathématiques
La valeur des chiffres Le sens des 4 opérations

Les ateliers consacrés à la numération s'étalent sur plusieurs semaines. La manipulation des verres et autres objets vise avant tout à permettre le développement de concepts. Les activités présentent donc des exercices favorisant la conceptualisation et la verbalisation et non les techniques de calcul. Il s'agit en fait de découvrir, pour mieux le comprendre, ce système qui constitue la base de l'apprentissage des mathématiques. Après seulement, on passera aux exercices écrits.

Dénombrement et regroupement

L'illustration de la page suivante a été utilisée pour vérifier la connaissance des nombres chez les participantes et les participants, mais l'objectif premier cherchait à démontrer l'avantage "du regroupement" pour compter plusieurs unités.

Ensemble, on a d'abord estimé "à l'œil" combien il pouvait y avoir de personnages en posant les questions suivantes: d'après vous, y a-t-il plus de 10 personnages? plus de 50? moins de 40? On a ainsi situé le nombre entre 20 et 40. Puis chacun devait, individuellement, trouver le nombre exact.

Bien que cet exercice paraisse au départ assez facile, un seul participant a trouvé le nombre exact de personnages. C'est le seul d'ailleurs qui a utilisé le regroupement. Toutes les autres personnes de l'atelier se sont trompées en comptant les figures une par une.

La personne ayant réussi a expliqué comment, en regroupant par 5 et par 10, elle était arrivée au bon résultat. Ainsi, elle faisait la preuve de l'avantage du regroupement et chaque personne a pu ensuite réussir l'exercice.

En discutant, à partir de l'illustration, les différentes façons de compter, cet exercice a permis aussi de vérifier certaines connaissances et de déceler les difficultés de chacun et de chacune. Il a surtout permis de découvrir et de comprendre "leur façon" de faire des regroupements.

Voici une série de questionnements qui peuvent être soulevés à partir de cette illustration:

• reconnaître visuellement les figurations du 2 -3- 4- 5- 6- 9;
• compter par 2, par 3, par 5, par 10;
• comment faire trois groupes égaux;
• combien de dix dans 20, dans 30;
• combien de cinq dans 20, dans 25, dans 30;
• une personne sur deux a les yeux bleus;
• une personne sur cinq a un enfant;
• une personne sur dix parle l'espagnol;
• etc.

Nous avons remarqué lors de cet exercice que certaines personnes avaient des difficultés à reconnaître visuellement les figurations des petits nombres tels qu'on les retrouve sur les dés ou les dominos. En questionnant leurs expériences pratiques de jeux, (un participant a eu beaucoup de difficulté à expliquer les règlements d'un jeu de cartes qu'il pratiquait assez régulièrement) nous pouvons constater comment le jeu peut aider à comprendre des règles, à organiser des données en plus de développer l'attention, la concentration et l'habileté au calcul mental. Cependant, nous croyons qu'il faut jouer assez régulièrement pour développer ces habiletés.

De l'observation

Mes stratégies pour compter

[Voir l'image pleine grandeur]

1. Le regroupement par 10, base de la numération

Objectif spécifique 1
Le regroupement par 10, base de numérisation

Afin de favoriser une compréhension suffisante du système de numération, nous avons continué l'expérimentation avec un autre exercice de regroupement. Il fallait cette fois effectuer, par manipulation, des regroupements qui permettraient de compter de grandes quantités d'objets. Il s'agissait, en somme, de susciter la découverte du principe de la numération à base 10.

Matériel:
pots de sous noirs ou de jetons (plusieurs centaines);
verres de plastiques ou contenants de différentes
grandeurs (2 ou 3 grandeurs pour le mille).

But de l'exercice
trouver un moyen rapide, et vérifiable sur demande, de compter un grand nombre d'objets sans se tromper.

Déroulement:

2 équipes ou plus.

Nous avons distribué à chaque équipe, des jetons ou des sous noirs (plusieurs centaines), dix petits verres et dix grands verres. Nous n'avons pas donné de consigne autre que celle de compter les sous et de les "regrouper" dans les verres. À la fin de l'exercice, il fallait donner la quantité de sous et prouver que le calcul était bon.

Questions

• Comment pouvez-vous assurer que vous avez trouvé le bon nombre et qu'il n'y a pas d'erreurs?
• Quel moyen avez-vous utilisé?
• Y a-t-il une façon plus facile que d'autres? Pourquoi?
• Pouvez-vous écrire le nombre au tableau?
• Que représente chacun des chiffres du nombre inscrit?
• Que veut dire le mot unité,...dizaine,...centaine? Pourquoi? (Découvrir le lien entre un et unité, dix et dizaine, cent et centaine.)
• Pouvez-vous ajouter et retrancher des unités, des dizaines et des centaines au nombre illustré et donner le nouveau nombre obtenu.

Résultat et commentaires

Le but de cet exercice était d'amener les participantes et les participants à rassembler les sous ou les jetons par groupes de dix que l'on plaçait dans un petit verre (la dizaine). Il fallait ensuite vider ou empiler les 10 petits verres dans un grand verre pour illustrer la centaine.

Ainsi on pouvait avoir 2 grands verres, 6 petits verres et 3 sous noirs pour 263 cents:

[Voir l'image pleine grandeur]

Il n'est pas évident que les personnes vont d'abord utiliser la base 10 et les verres pour compter les objets. En effet, l'une des deux équipes ne s'est donné aucune directive de départ et chaque individu a compté une poignée de sous qu'il plaçait dans un verre avec, pour résultat, qu'il était impossible de dire quelle quantité de sous contenait un verre, grand ou petit. Il fallait estimer au poids pour savoir s'il y avait 50, 75 ou 100 pièces.

Le groupe a alors adopté une démarche en convenant de mettre 50 sous dans les petits verres et 100 dans les grands verres. Cependant, si on ajoutait ou enlevait une poignée de sous, il fallait reprendre le calcul. Tout ça devenait long et compliqué.

Après d'autres manipulations et discussions, nous avons trouvé une méthode plus pratique: dans les grands verres, on plaçait 100 sous, dans les petits 10 et le reste à côté, pour enfin constater l'utilité de ce regroupement et faire le lien avec l'écriture des nombres.

Il y a beaucoup davantages à employer des verres en plastique. D'une part, ils ne coûtent rien ce qui permet à chaque individu d'avoir son propre matériel. De plus, le regroupement n'est pas déterminé d'avance, il faut le structurer, l'organiser soi-même: on empile facilement dix petits verres dans un grand pour illustrer et constituer la centaine. Cette manipulation prépare et ouvre la voie à la compréhension des algorithmes d'opérations, entre autres la soustraction avec emprunt: par exemple lorsqu'il y a un zéro au rang des dizaines [208 - 189], on doit emprunter une centaine qui peut être séparée en 10 dizaines. Enfin, il est facile de passer au stade semi-concret en dessinant un grand rectangle pour représenter le 100 et un petit rectangle pour le dix.

Cet exercice doit être refait plusieurs fois en utilisant des regroupements semi organisés et organisés. On présentera, par exemple, des regroupements par 2 et par 5. On peut utiliser des objets à l'unité avec des objets attachés par 10 ou par 25. Ou encore des paquets plus complexes 27, 32, 18 anneaux avec des anneaux à l'unité.. On peut aussi utiliser des crayons, mais on est vite limité par le nombre. Cependant la représentation de la centaine (la boîte) et de la dizaine (un paquet) est plus facile parce que plus réel. Chaque exercice permet de déceler les difficultés et de pratiquer les calculs appropriés (compter par 2, 5, 20 etc).

2. La lecture et l'écriture des nombres

Objectif spécifique 2
La lecture et l'écriture des nombres (avec les verres)

Le travail s'est fait d'abord au tableau, en grand groupe.

Il fallait écrire au tableau un nombre choisi par le groupe, puis expliquer la valeur des chiffres, selon leur position, en se servant des verres comme soutien à l'explication.

Pour ce faire, on plaçait sous les chiffres inscrits au tableau: les grands verres pour les centaines, les petits verres pour les dizaines et les sous pour les unités (les verres étaient placés sur le bord du tableau). Cette manière d'illustrer le nombre en facilitait la lecture.

Exemple: le nombre 247

[Voir l'image pleine grandeur]

De cette façon, en lisant le nombre illustré, on donnait d'abord le nombre de centaines en indiquant les grands verres: 2 pour deux 100; par la suite, on indiquait 4 pour quatre 10 et 7 pour sept unités.

Les nombres 70-80-90 amènent beaucoup de confusion chez plusieurs participants et participantes car la formulation verbale est différente de la représentation écrite. On profitera donc de cet exercice pour illustrer et nommer les nombres entre 70 et 100.

Ainsi 71 c'est 6 petits verres et 11; 94, c'est 8 petits verres et 14. On illustrera de même le 80 en empilant les verres 2 par 2 pour avoir 4 groupes de 20, tout en insistant sur la différence entre l'écriture et la lecture.

Le travail se poursuit en équipe de deux: une personne fait le portrait d'un nombre avec des verres; l'autre personne doit dire et écrire le nombre représenté.

Puis, individuellement, chaque personne devait faire le portrait du nombre donné par un ou une participant-e ou par l'animatrice.

Le rôle et la place du zéro dans le nombre

On peut très bien expliquer le rôle et l'importance du zéro dans les nombres à laide des verres. Si on demande, par exemple, de représenter avec les verres le nombre 209, on réussit en général assez facilement. Pourtant, quand on demande d'écrire le nombre, on voit souvent le nombre écrit ainsi: 2009. Il faut, pour corriger cette erreur, comprendre que le mot cent lorsqu'on "dit" le nombre deux cent neuf, indique la valeur et la place du 2. De plus, il importe de faire remarquer qu'il ne faut pas plus de 3 chiffres pour écrire les nombres jusqu'à 999.

Parce qu'on retrouve avec le "mille", les mêmes difficultés d'écriture qu'avec le "cent" (on écrit 34 000 876 au lieu de 34 876), on peut introduire à cette étape, la lecture et l'écriture des nombres plus grands que mille. Il suffit d'ajouter un contenant plus grand, lequel pourra contenir 10 verres de cent.

Pour l'illustrer, il faut compter par 100 jusqu'à "dix cents", puis placer les 10 verres dans un contenant plus grand (des contenants de 1 litre de yogourt ou de crème glacée font très bien l'affaire).

On peut aussi, en utilisant plus de 10 grands verres, démontrer la similitude entre douze cents et mille deux cents:

[Voir l'image pleine grandeur]

La "reconnaissance auditive" dans l'écriture des nombres

Il faut beaucoup de mots pour dire un nombre. Ainsi il faut 7 mots pour "dire" le nombre 2 879 et 4 chiffres pour "l'écrire". Il est donc important de découvrir la différence entre la formulation verbale et l'écriture des nombres. Cet exercice est justifié entre autres pour les personnes immigrantes qui rencontrent plusieurs difficultés avec la numération parlée.

Nous avons alors fait des exercices de "reconnaissance auditive":

Dans chacun des chiffres, il y a un zéro. En écoutant bien les mots, tu pourras dire si c'est l'unité, la dizaine ou la centaine qui "manque dans le nombre":
2 820 - 6 409 - 12 053 -102 371 - 9 200 - 10 000

L'écriture et la lecture des grands nombres présentent un intérêt particulier. Le gros lot de la 6/49 avec ses millions fait rêver tout le monde et on voudrait bien savoir comment écrire dix millions. Mais c'est surtout lors de la présentation des états financiers du groupe qu'on découvre l'importance de savoir lire et écrire les nombres. (Les revenus et les dépenses étaient écrits sur des cartons et les gens devaient les lire).

Cependant, il faut aussi expliquer la valeur de ces nombres. Ainsi, $10,000, c'est 10 billets de $1000 et $100,000, c'est 100 billets de mille. En fait, il faut inventer des situations pour imaginer les grands nombres (des piles de dictionnaires par exemple) et en comprendre la valeur.

Après les exercices de manipulations, nous passons au stade semi-concret pour vérifier la compréhension.

Le portrait du nombre

Exercices

Quel nombre est représenté par...

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Fais le portrait du nombre.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Comment écrire le nombre qui a...

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Le passage à la dizaine suivante ( + 1, - 1 )

• Placer sur la table 5 petits verres et 9 jetons. Puis ajouter un jeton.
• Que se passe-t-il lorsque j'ajoute 1 jeton?
• Qu'est-ce que je peux faire avec les dix unités?
• Que se passe-t-il si je place les 10 jetons dans un verre?
• Quel est le nouveau nombre?
• Comment s'écrit ce nombre?

Cet exercice implique un éventail assez complexe de relations et de propriétés d'opérations dont il ne faut pas sous-estimer l'importance et la difficulté. En ajoutant une unité au nombre 59, ce sont les principes du regroupement par 10, de l'addition et de la retenue qui entrent en ligne de compte. Cela fait appel aussi à la compréhension de la valeur positionnelle et à la perception du nombre. Il faut amener à la visualisation et à la verbalisation du nombre 60, comme étant 59 et 1 ou 50 et 10 ou encore 5 dizaines (verres) et 10 unités pour enfin arriver à 6 dizaines et zéro unité.

On fera la même chose avec le moins 1

• J'ai 9 petits verres.
• Combien ça fait de jetons?
• Comment ça s écrit?
• Que se passe-t-il si j'enlève 1 jeton?
• Comment l'illustrer?
• Que reste-t-il?

Chaque personne refait des exercices de manipulation avec des nombres différents et explique sa démarche.

Faire composer des problèmes pour illustrer ces situations.

• Je pèse 179 lbs et je grossis d'une livre.
• J'ai 69¢ et j'ajoute 1¢.
• J'ai 6 billets de $10 et 10 pièces de $1.
• Il me manque $1 pour avoir $200. Combien j'ai d'argent?

Le passage à la dizaine suivante suppose qu'on connaît bien la suite des nombres mais aussi qu'on garde en mémoire le chiffre de départ. Dans les nombres en dessous de cent, les personnes ne rencontrent pas trop de difficultés. C'est plutôt dans le calcul de nombres plus grands qu'apparaissent les complications. Supposons qu'à 265, nous devons ajouter 6. Sans support visuel, on calculera ainsi 66, 67, 68, 69,.70, 71 en oubliant le 200. Souvent aussi, le calcul se fait à partir de 65 comme dans le calcul des heures de la gardienne (module du temps). Si le calcul se fait avec les verres, il sera plus facile de voir le nombre en entier et de compter en gardant en tête le 265 du départ.

Il faut demander au groupe de composer des problèmes où il doit ajouter et enlever des petits nombres. Puis, on habituera les gens à retenir le chiffre de départ comme base de calcul sans le support des verres.

Chercher l'erreur

Dans cette liste, il y a 2 chiffres qui ne se suivent pas. Peux-tu les trouver?

19 - 20	9 - 10	79 - 80
39 - 40	59 - 60	49 - 50
69 - 80	29 - 30	89 - 90

Pourrais-tu compléter la suite...

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

3. La régularité des nombres et le calcul par 10

Objectif spécifique 3:
La régularité des nombres et le calcul par 10

Des exercices de manipulation, avec des verres d'abord et les sous ensuite, peuvent aider à découvrir la régularité dans les nombres et ainsi faciliter le calcul.

Placer sur la table un paquet de 10 crayons et 5 crayons à l'unité. Ajouter ensuite un paquet de 10, puis un autre et ainsi de suite, ce qui donne 15-25-35-45 etc.

Demander à une personne d'écrire au tableau les nombres un en dessous de l'autre, au fur et à mesure de l'ajout, pour découvrir la régularité et le sens de l'opération.

Refaire l'exercice de manipulation en partant d'un nombre différent et compléter jusqu'à la centaine suivante
Exemple: partir de 45, 55, 65, 75, 85, 95, 96, 97, 98, 99, 100

On pourra ensuite écrire sur une feuille la suite des nombres en colonne puis en ligne (compter par 10 puis par 1 ) et les lire

Il est possible également, à la suite de cet exercice, de construire un tableau des nombres de 1 à 100 (voir la grille de la page suivante).

Tous ces exercices visent à développer l'habileté en comptage et préparent à l'addition et au calcul du change.

La grille des nombres

[Voir l'image pleine grandeur]

Imprimer la Grille des nombres

Le dictionnaire comme outil d'apprentissage

L'utilisation du dictionnaire au cours de l'atelier de calcul n'était pas évident au premier abord. Cependant, en s'attardant un peu à cette idée, on peut voir facilement à quel point cet outil peut être intéressant. Utilisé pour poursuivre 1 apprentissage de la numération, avec l'ordre et la suite des nombres, on a donné un sens signifiant à l'apprentissage.

Ici, c'est le nombre vu sous son aspect ordinal. En effet les nombres servent aussi à ordonner, à donner un rang, un ordre aux choses. C'est un sens différent de celui qui consiste à exprimer la quantité d'unités que comportent une collection, un ensemble. C'est aussi une utilisation des nombres qui diffère de celle servant à compter de l'argent.

On peut en arriver, à l'aide de cet outil, à la perception d'un certaine invariance des nombres et à la compréhension de la régularité de ceux-ci.

De plus, en liant l'ordre des nombres à l'ordre des lettres de l'alphabet, on introduit deux apprentissages qui se complètent, qui se greffent l'un à l'autre pour une meilleure compréhension de l'un et de l'autre.

En utilisant le dictionnaire, on pourra:

• découvrir la relation d'ordre dans les nombres;
• découvrir les nombres pairs et impairs;
• pratiquer la lecture et l'écriture des nombres;
• initier aux chiffres romains.

Démarche

Chaque personne avait en main un dictionnaire pour faire l'exercice.

Comme c'était, pour la plupart des participants et des participantes, leur premier contact avec le dictionnaire, on a d'abord pris le temps de le feuilleter, de l'étudier. Puis on a essayé de lire des mots dont, entre autres, le nom du dictionnaire. On s'est ensuite penché sur la façon de chercher dans le dictionnaire.

On a de la sorte découvert qu'il contenait des mots mais aussi des chiffres, et que ces chiffres correspondaient à l'ordre des pages. C'était en fait la découverte d'une nouvelle utilisation des nombres. En effet, en plus d'indiquer la quantité de pages contenues dans le livre, les chiffres deviennent un repère pour retracer l'ordre alphabétique et les mots

Les chiffres romains

Si on regarde au début du dictionnaire, on retrouve des signes différents: les chiffres romains. Ces symboles n'étaient pas tout à fait inconnus des participants et des participantes (on les voit parfois sur des montres ou des horloges). Nous les avons donc abordés comme un autre système de numération, sans s'y attarder cependant plus qu'il ne faut.

En suivant l'ordre des pages, il a été facile de déduire la valeur des signes utilisés et les règles qui les régissent (valeur additive et soustractive).

Exemple:
valeur additive: XVIII, c'est 10 + 5+1 + 1 + 1
valeur soustractive: IX, c'est 10-1

La relation d'ordre dans les nombres

En cherchant dans le dictionnaire certaines pages identifiées, on peut vérifier, chez les participantes et participants, les connaissances spontanées des notions de sériation et d'ordre des nombres, d'ordre croissant et décroissant et, de ce fait, la compréhension du nombre.

Par exemple, en cherchant la page 159 dans le dictionnaire, il faut comprendre où se situe ce nombre dans la suite et l'ordre des pages. Cette page sera-elle au début ou à la fin du livre? Vient-elle avant ou après la page 170, etc.?

Autre exemple: je suis à la page 1099 et je veux aller à la page 1145, dans quel sens dois-je tourner les pages? Ce nombre est-il situé avant ou après 1099?

Voici des idées d'exercices qu'on peut faire pour développer la compréhension du nombre:

• Par quelle lettre commence le mot inscrit en haut de la page 893?
• Quelle illustration retrouve-t-on à telle page?
• Une personne donne un nombre compris entre le début et la fin du dictionnaire; il faut trouver cette page.
• On essaie d'ouvrir le dictionnaire le plus près possible de la page 1000, etc., etc.

Les chiffres pairs et impairs

En tournant les pages du dictionnaire, on a pris conscience dune autre forme de régularité. Les pages 1,3,5,7,9, etc sont toutes sur le même côté et les pages 2,4,6,8,10, etc sont de l'autre (comme les numéros civiques). Ainsi, avant de trouver le numéro d'une page, on essayait de dire d'abord de quel côté il allait se situer: à gauche ou à droite?

La lecture et l'écriture des nombres

Enfin, on s'est servi du dictionnaire pour apprendre à lire et à écrire ce qui, dans la suite des nombres, cause le plus de difficultés. En ce sens, on fera lire et observer la suite des nombres à partir de certaines pages telles 999, 1000, 1001, 1002 et ainsi de suite.

De plus, que l'on parte de 100, de 200, de 800 ou de 1000, on aura toujours un même ordre, c'est-à-dire 101 ,...201 ,...801, 1001...

L'ordre alphabétique

Pour terminer, on a relié l'ordre alphabétique à l'ordre des chiffres en cherchant à quelle page commençait chaque lettre de l'alphabet.

Le dictionnaire - Des chiffres et des lettres

Indique le numéro de la page où commence chaque lettre de l'alphabet.

[Voir l'image pleine grandeur]

Imprimer la Grille des nombres

4. La valeur positionnelle et additive

Objectif spécifique 4
La valeur positionnelle et additive

Les exercices qui suivent visent particulièrement à faire saisir la position et la valeur des nombres et à distinguer, l'une de l'autre, l'unité, la dizaine et la centaine, de façon à mieux comprendre ce qui se passe lorsque l'on additionne des nombres. Les personnes ont souvent des problèmes à classifier ou ordonner les chiffres et les nombres. On vise donc ici à découvrir la valeur réelle des nombres en jeu, ce qu'ils contiennent et la place (signifiante) qu'ils occupent dans l'addition.

Nous avons travaillé ces notions en exploitant des exercices de manipulation et d'observation pour pouvoir, graduellement, effectuer le passage aux symboles écrits.

Matériel
des jetons à l'unité, des petits verres (10) et des grands verres (100)

Démarche
L'activité se fait en grand groupe mais chaque personne a en sa possession le matériel qu'il peut manipuler.

Faire le portrait de 123.
J'ajoute 1 jeton +1 + 1 + 1 + 1...
Qu'est-ce qui change?
Qu'est-ce qui ne change pas?
Qu'est-ce que j'ai fait?
Je compte par 1 (j'ajoute des unités aux unités).

Faire le portrait de 123.
J'ajoute 1 petit verre +1 + 1 + 1
Qu'est-ce qui change?
Qu'est-ce qui ne change pas?
Qu'est ce que j'ai fait?
Je compte par 10 (j'ajoute des dizaines aux dizaines)

Faire le portrait de 123.
J'ajoute 1 grand verre +1 + 1 + 1
Qu'est-ce qui change?
Qu'est-ce qui ne change pas?
Qu'est ce que j'ai fait?
Je compte par 100 (j'ajoute des centaines aux centaines).

Reprendre le même exercice oralement à plusieurs reprises, car il prépare à la compréhension de la position des chiffres dans l'addition de plusieurs nombres. Par la suite, on pourra introduire parallèlement l'écriture algorithmique de l'opération et expliquer la position et la valeur des chiffres ainsi que le rôle du zéro.

Composer des problèmes où l'on retrouve des situations semblables.

Exemples:
Je compte mon change: j'ai 13¢ + 10¢+10¢ +10¢+10¢. J'ai $12. Que faut-il ajouter pour me rendre à $52?

J'ai donné $25 d'acompte sur l'achat d'un divan. À chaque mois, je donne $10. Qu'est-ce que j'aurai déboursé au bout de 6 mois?

Exercice d'observation

Observe bien les nombres dans chaque suite.
Qu'est-ce qui change? Qu'est-ce qui ne change pas?
Quel nombre ajouterais-tu à la suite?

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

L'addition en portrait

Écris la réponse en signes puis en chiffres.

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

L'addition

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Pratique tes additions.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

5. Initiation à la multiplication

Objectif spécifique
Initiation à la multiplication

À cette étape du cheminement de formation en calcul, nous avons utilisé l'addition répétée d'un même nombre pour introduire la notion de multiplication. Nous nous sommes également servi du regroupement d'objets divers comme support à l'apprentissage du calcul par 10.

La manipulation et l'observation facilitent à nouveau la compréhension de cette nouvelle notion. De plus, l'addition répétée, qui implique un travail plus long, permet d'initier la multiplication simplement car celle-ci peut être vue comme un moyen de résoudre certains types de problèmes plus facilement ou plus rapidement.

Démarche

• Placer sur la table 7 paquets de 10 feuilles.
• J'ai combien de paquets?
• J'ai combien de feuilles par paquets?
• J'ai donc 7 paquets de 10 feuilles.
• J'ai 7 fois 10 feuilles.
• Que fait 7 fois 10?

Introduire le mot fois et indiquer comment ce mot se traduit en signe mathématique: le X.

Comme les emballages de 10 (cassettes, cartons de cigarettes) deviendraient trop dispendieux, il est possible, par exemple, de former des regroupements par 10 dans des sacs de papier. Des dessins ou des mots sur une feuille feraient aussi l'affaire. Utiliser aussi des $10 et des 10$. Il s'agit, en fait, d'avoir une bonne variété d'objets, ce qui facilite aussi le transfert.

Chaque personne doit refaire l'exercice de manipulation avec des quantités différentes et expliquer sa démarche.

De plus, elle doit traduire cette manipulation en langage mathématique.

Lorsqu'une personne explique sa façon de faire, on reprend oralement l'opération inverse (initiation à la division) avec ces questions:

• Combien a-t-il fallu de paquets de 10 pour avoir 70 feuilles?
• Combien de 10 dans 70?
• Quel chiffre m'indique le nombre de paquets de 10?

Faire remarquer qu'en observant le nombre écrit, on peut facilement découvrir la réponse à cette question.

Dans l'exemple 140, j'ai 14 verres de 10 ou 14 x 10.

On pourra ensuite travailler avec des représentations semblables.

[Voir l'image pleine grandeur]

Les problèmes illustrés

Le problème illustré a été utilisé pour simplifier l'apprentissage chez les personnes qui ont de la difficulté avec l'écrit. En effet, le problème illustré permet de visualiser l'ensemble de la situation sans avoir recours à la lecture. L'illustration des données favorise ainsi une meilleure compréhension de la question et facilite la mémorisation de ces mêmes données.

De plus, comme tout problème, le problème illustré implique des raisonnements qui demandent d'établir des relations entre les quantités en cause, de connaître et comprendre le rôle, le sens, la portée et les effets des diverses opérations. Par la suite, viendront les techniques de calcul.

Nous présentons ici un problème à opérations multiples. Cependant, pour éviter certains blocages au niveau de la compréhension du sens et des techniques des opérations, nous avons fait des exercices préalables à la compréhension entre autres de la retenue et de l'emprunt.

La retenue et l'emprunt découle d'une même connaissance, c'est à dire la reconnaissance ou la perception des groupes de 10 (la dizaine) dans les nombres, surtout dans les nombres de 11 à 19. (Cette perception n'est pas évidente pour tous, on alignera 12 unités plutôt que d'utiliser le regroupement de 10 et 2).

La perception auditive du 10 dans les nombres 17 18 et 19 est facile et pourtant plusieurs participant-e-s ne font pas le lien entre 18 et 10 et 8.

I1 faut questionner et faire prendre conscience du 11 comme étant un 10 et 1, 12 un 10 et 2 ainsi de suite jusqu'à 19 et même plus loin, deux 10 et 2 pour 22

Nous avons donc travaillé cette notion avec des exercices simples en demandant aux personnes d'indiquer la réponse à l'aide de symboles

Combien de personnes dans chaque atelier

[Voir l'image pleine grandeur]

En plus de la représentation visuelle du 10 dans le nombre 11, 12, 13, nous constatons que les participants font vite et oralement le total des personnes des 4 ateliers. On "voit" l'avantage de cette représentation

Cependant, il faut transférer cette perception, c'est à dire amener les gens à garder mentalement cette représentation pour d'autres situations et surtout pour les situations opératoires où la retenue et l'emprunt sont en cause.

Pour développer cette perception, il ne faut pas hésiter à travailler parallèlement le calcul écrit et la représentation symbolique.

[Voir l'image pleine grandeur]

Lorsque cette notion est acquise nous passons au problème.

Le problème part d'une situation vécue par les personnes de l'atelier Cette situation concrète amène un intérêt particulier à la résolution des différentes questions soulevées.

Voici les données du problème:

La semaine dernière nous sommes allés à Duchesnay. Plusieurs personnes ont participé à cette activité. En plus des participants et des participantes, il y avait 6 animatrices, 2 amis et 1 bénévole. Le club social a loué un autobus au coût de $140 pour transporter tout le monde. Parce que Sinoun a mal au cœur en autobus, Monique a utilisé son auto et a amené avec elle trois personnes. Chaque personne a déboursé $2 pour le voyage et le club social a financé la balance.

Question: combien doit débourser le club social?

Pour bien comprendre les données, nous posons d'abord ces questions:

Qui est allé à Duchesnay? Est-ce qu'il y avait beaucoup de monde?
Est-ce que l'autobus était plein?
Combien de personnes environ?
Est ce qu'il y avait plus d'hommes que de femmes?
Croyez-vous que $2 par personne c'est suffisant pour payer l'autobus?
(Une évaluation de la distance pourrait aussi se faire à partir de ce problème.)

Tableau 1 - Le monde d'Atout-Lire

Avec ce premier tableau, nous allons chercher combien de personnes ont participé à l'activité (les oui). Le premier chiffre indique le nombre de personnes de chaque atelier et inclus l'animatrice.

[Voir l'image pleine grandeur]

Il faut ajouter les 2 amis et la personne bénévole qui ne sont pas inclus dans ces données.

À cette première étape nous nous assurons de la connaissance des additions et soustractions de base.

Tableau 2 - La sortie à Duchesnay

[Voir l'image pleine grandeur]

L'illustration montre l'ensemble de la situation. Tout le raisonnement se fait d'abord à partir du tableau. On ne cherche pas la réponse mais comment faire pour arriver à la réponse.

Les données sont complétées ensemble.

On regroupe pour calculer le nombre de personnes.

Avec des crayons de couleurs différentes, on identifie les animatrices, les amis et la personne bénévole.

Des flèches relient 4 personnages à l'auto. Le coût du transport est indiqué sous l'autobus.

Les questions suivantes en rapport avec l'illustration permettent de bien situer les données, de faire des liens, d'établir des relations entre les quantités en cause (par exemple: $2 par personne et 32 personnes).

Que représentent les petits personnages?
Que faut-il faire pour trouver le nombre de participants et de participantes seulement?

Que faut-il faire pour trouver le nombre de femmes si je sais qu'il y avait 13 hommes?
Monique a utilisé son auto et a amené 3 personnes avec elle.
Quelles personnes ont fait le voyage en autobus?
Chaque personne a payé $2. pour le voyage.
Combien de $2 le club social a-t-il ramassé?

Tableau 3 - Les données du problème

Les données sont identifiées avec des chiffres. Les personnes doivent identifier ces données et découvrir les effets des opérations qu'on peut effectuer sur ces nombres.

[Voir l'image pleine grandeur]

Les mêmes questions sont reprises cette fois avec les chiffres.

Que représentent les 19 femmes et les 13 hommes?
Quelle opération faut-il faire pour trouver le total, le tout?
Est-ce qu'on peut faire une soustraction, un moins avec ces données?
Qu'est-ce qu'on trouverait en faisant une soustraction?
Que représentent ces $2?
Peux-tu dire, sans les compter, combien il devrait y en avoir? Etc.

Nous avons travaillé avec ce problème durant trois ateliers. Après avoir expliqué le sens des opérations d'addition, de soustraction et de multiplication, nous avons mis l'accent sur la technique des opérations

Cependant, nous constatons que certaines personnes éprouvent beaucoup de difficultés avec le calcul écrit. Un peu comme en français, lorsque l'accent est mis sur le décodage de la technique, il s'en suit une perte du sens global.

Pour ces personnes nous croyons qu'il serait préférable de travailler avec la calculatrice afin de garder tout son sens aux opérations et aux résultats.

Par contre, certaines personnes ont compris et amélioré leur calcul écrit. Par exemple le calcul des $2.a permis à certaines personnes de comprendre le sens de la multiplication et l'avantage d'utiliser cette opération.

Une personne entre autre pour qui le calcul des $2 s'est avéré une suite de calculs longs et difficiles a découvert avec surprise qu'elle pouvait tout aussi bien multiplier

Voici sa méthode. La base de calcul de cette personne est le 5.

2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $
2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $
2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $	2 $

2 + 2 + 2 font 6
6 + 6 + 6 c'est 5 + 5 + 5 plus 3 égalent 18 puis elle continue avec une autre tranche de 18

18+18 c'est 10 + 10 + 5 + 5 + 3 + 3 = 36 pour poursuivre par l'ajout de 12 puis de 6, 6 et 4 pour un total de 64.

Il est bien évident que le calcul 32 x 2 permet d'arriver au même résultat avec beaucoup moins d'efforts et de risques d'erreurs.

Pour assurer le transfert des acquis, nous avons présenté un problème semblable mais dans une situation imaginée.

Ensuite, nous demandons aux gens de composer et de dessiner eux-mêmes un problème semblable ce qui permet de revoir et d'approfondir les notions.

Problèmes à discuter

Micheline va à la caisse changer un chèque de $660.
La caissière lui remet la somme en $100. Combien aura-t-elle de cent dollars?
Si la caissière lui remet la somme en $10, combien aura-t-elle de dix dollars?
En te basant sur le nombre de $10 reçus, pourrais-tu dire combien de $20 il faudrait pour faire $660?

J'ai 1320 crayons en paquets de 10.
Je place mes paquets de 10 dans des boîtes de 100, puis je place mes boîtes de 100 dans des grandes boîtes de 1000.

[Voir l'image pleine grandeur]

Résultat et commentaires

La compréhension implique la découverte de relations et de régies.

Partant de ce principe, et de l'expérimentation que nous avons réalisé, il nous faut maintenant questionner la pertinence des exercices que nous avons proposés ainsi que l'ordre dans lequel nous avons procédé pour atteindre les objectifs visés.

En fait, tout ce travail de manipulation visait à développer le concept du nombre et de la numération puis à saisir les principes du système. Cependant, pour découvrir les corrélations et les lois qui engendrent la compréhension d'un système, il faut certaines connaissances préalables.

Ainsi, un seul participant qui avait déjà acquis les techniques écrites des opérations a exprimé clairement qu'il comprenait désormais le sens de la retenue et de l'emprunt. Le matériel utilisé (les verres ) lui a permis de "voir" ce qui se passait quand on retient ou emprunte 1 au rang des dizaines ou des centaines. Cette personne a pu faire un cheminement à partir de ce qu'elle savait déjà et établir des liens entre l'expérimentation visuelle qui lui était proposée et la mécanique de calcul qu'elle avait développée.

Pourtant nous croyons essentiel de passer par cette étape même si le résultat n'est pas toujours évident. Le développement de concepts et de relations exige des expériences nombreuses et variées. Les difficultés spécifiques rencontrées par les gens nous obligent à revenir souvent sur les mêmes données si on veut développer et faire saisir ces concepts et ces relations. (C'est pourquoi nous retrouvons sous une forme différente des exercices semblables à ceux vus dans les autres documents). Pour que les notions soient bien intégrées, il faudra toujours revenir à cette visualisation, (référence aux verres et aux objets) et rattacher les nouveaux apprentissages à ce qui a été vu dans ce module.

Dans l'ensemble, nous avons pu constater que les gens maîtrisent mieux la lecture et l'écriture des nombres. En plus nous croyons qu'ils ont clarifié le sens des opérations. Pour s'en assurer nous leur avons demandé d'inventer des problèmes à partir d'illustrations.

Ceci est l'exemple d'un problème composé à partir d'une illustration de pointes de fromage. Cette personne travaillait à l'occasion chez un dépanneur ce qui explique le choix de l'illustration.

[Voir l'image pleine grandeur]

Voici les données de son problème. Le lundi, je remplis le frigidaire. Je mets 15 fromages blancs et 3 jaunes parce qu'on vend plus de blancs. On vend plus de fromage le jeudi et le vendredi. Lundi on en vend 3, mardi 4, mercredi 2, jeudi 5 et vendredi 3. Il en reste combien?

Avec ces données, nous avons travaillé les soustractions simples:
18 - 3, 15 - 4, 11 - 2, 9 - 5, 4 - 3 et trouvé le reste.

Nous avons aussi constaté qu'on pouvait trouver le reste en soustrayant le total des fromages vendus dans la semaine 18-13 + 4 + 2 + 5 + 3 1

De plus, nous avons vérifié notre calcul en cherchant si le total des fromages vendus plus le reste nous donne bien le nombre de fromages qu'on avait au départ.

À partir de l'illustration, nous avons appris le calcul ainsi que la multiplication par 3 et par 6.

Le travail avec des dessins permet de vérifier la compréhension des notions abordées. Il développe aussi le langage mathématique, le vocabulaire utilisé étant lié au sens et aux signes des opérations à effectuer puisque que les gens doivent composer les données.

Parfois les données portent à confusion. Cette fois, une participante devait trouver une situation pour expliquer l'opération 9-4. Ses données, il y a 9 hommes et 4 femmes, n'amenait pas l'idée de la soustraction. II a fallu questionner, développer le sens pour arriver au problème suivant: si on va danser, il manque des femmes pour faire des couples. Nous avons alors insisté sur ce sens de comparaison de la soustraction et porté une attention particulière aux expressions de plus et de moins.

Enfin nous constatons qu'il est difficile de changer certaines habitudes de calcul. Par exemple, la majorité des personnes de l'atelier sont habituées à calculer des petits nombres sur leurs doigts. Bien que nous ayons expliqué et travaillé concrètement la dizaine avec les verres, les gens revenaient quand même à cette forme de calcul dans l'addition 10 + 6 et même avec 10 + 8. Comme l'explique si bien Yvon Deschamps, la logique des mathématiques c'est facile...

Travailler avec du matériel concret n'amène pas automatiquement l'élaboration de concepts. Mais la répétition, la verbalisation et la création d'images mentales aideront les participants et les participantes à mieux saisir les principes de ce système et à organiser tous ces éléments dans un ensemble cohérent.

Module 3 – Le budget et l'argent

Budget: n. m. (mot angl: de l'anc. fr. bougette. petite bourse). État de prévision des recettes et des dépenses d'un pays, d'un département, d'une commune, d'une entreprise, d'une famille, d'un particulier.

La question de l'argent s'avère évidemment une préoccupation essentielle chez les personnes qui participent aux ateliers de calcul. Au moment de l'identification des besoins, elles exprimaient clairement leur intérêt à développer de nouvelles connaissances pratiques sur plusieurs plans à la fois: le travail à partir des billets et de la monnaie, le calcul du change, les chèques, les factures, les taxes, le logement, le budget étaient autant d'éléments considérés comme importants et que les gens voulaient retrouver dans leur démarche d'apprentissage.

Selon le niveau d'avancement de chaque personne, les priorités sont différentes. Par exemple, certaines personnes gèrent elles-mêmes leur budget alors que d'autres ont recours à la famille ou à des ami-e-s pour les aider; c'est ainsi que les activités d'apprentissage doivent correspondre à des besoins variés en proposant divers exercices dont le degré de difficulté est plus ou moins élevé.

Le travail sur l'argent et le budget fournit un contenu d'apprentissage signifiant car les activités, et les nouvelles connaissances qu'elles incluent, s'intègrent facilement à l'expérience déjà acquise par la plupart des personnes. Ces dernières peuvent alors aisément faire référence à leur savoir propre et associer ce qu'elles apprennent à un aspect présent, connu en tout ou en partie, de leur réalité quotidienne.

Les exercices compris dans ce module sont construits et s'appuient sur la pratique des gens. Nous voulons explorer davantage ou approfondir le champ du connu par divers outils de formation qui, de plus, rendent possible l'établissement de liens entre le contenu de l'apprentissage et la structure cognitive des gens qui participent aux ateliers. Il s'agit, en fait, de profiter du bagage de connaissances qu'ont développé les personnes: partir de ce qu'elles possèdent pour aller plus loin.

Ce module sur l'argent et le budget contient des activités complémentaires à celles que l'on trouve dans la numération. Nous y intégrons des exercices qui favorisent:

• l'observation et la manipulation;
• la lecture, l'écriture, l'estimation et le calcul de montants d'argent (on travaille en premier lieu avec des billets, des chiffres "ronds", pour ensuite voir les montants comprenant des cents);
• la pratique des quatre opérations;
• le budget (le vocabulaire, la soustraction, la division etc.).

Les connaissances sont donc introduites par le biais d'activités qui se rapportent aux situations courantes. Nous tentons de développer une variété d'exercices pour chaque nouveau concept de façon à susciter le transfert des notions: plus les expériences sont variées, plus elles rendent possible la construction d'un concept par généralisation.

À travers ce thème, nous intégrons des notions mathématiques qui, d'une part, rejoignent, répètent ou examinent davantage celles déjà incluses dans d'autres modules et, d'autre part, constituent une initiation à de nouveaux concepts mathématiques.

Somme toute, le but de ce module est de favoriser l'acquisition et l'approfondissement d'habiletés concernant les questions d'argent et de budget de manière à posséder les acquis nécessaires pour répondre à ses besoins. Mais il cherche également à ce que les personnes développent, en partie du moins, leur propre mécanisme de résolution de problèmes relatifs à l'argent.

Objectif général
Se familiariser avec la notion de budget et développer ses habiletés à manipuler et calculer l'argent.

Objectifs spécifiques

1. Lire, écrire et manipuler des montants d'argent
2. Initier au budget
3. Comprendre le sens et le rôle du point

Notions mathématiques contenues dans ces apprentissages
Le langage et les symboles mathématiques
La valeur des chiffres
La soustraction
La division

Dans ce module, nous appliquons les apprentissages du système de numération au calcul de l'argent. Ainsi, les objectifs concernant la numération se poursuivent ici. Le modèle de l'argent est utilisé pour approfondir ce qui a été vu et pour établir des liens entre ce qui est connu et les nouveaux apprentissages. Les concepts régissant le système monétaire sont intégrés à cette étape. Les activités de manipulation et d'observation sont encore utilisées pour introduire les notions de base et expliquer l'algorithme des quatre opérations en accordant cependant plus d'importance à la soustraction et à la division. Le matériel utilisé (l'argent de papier, reproduction de billets de banque, et la monnaie) sera mis en parallèle avec les verres utilisés dans le premier module. C'est aussi à cette étape qu'on introduira la calculatrice comme support à l'apprentissage. D'autre part, tout au cours de ce module, on tentera de découvrir la régularité dans le calcul de l'argent.

1. Lire, écrire et manipuler des montants d'argent

Objectif spécifique 1
Lire, écrire et manipuler des montants d'argent

Exercice
changer un chèque

Matériel
des chèques et de l'argent de papier

Fonctionnement
en équipe de 2

[Voir l'image pleine grandeur]

Pour introduire ce module, nous avons distribué un chèque et de l'argent de papier à chaque équipe. Le chèque était fait au nom de la personne et les montants étaient différents mais tous plus gros que $100.

• Dans un premier temps ceci a permis de voir comment rédiger un chèque.
• Puis nous avons comparé les montants d'argent:
• Qui a reçu le plus gros montant? le plus petit montant?
• Peut-on les mettre en ordre croissant? décroissant?

Nous avons demandé ensuite de changer le chèque en utilisant l'argent de papier. Aucune consigne n'est donnée, l'équipe choisit les regroupements qu'elle fera avec les billets.

Il faut s'assurer que chaque groupe a suffisamment de billets de $100, de $50, de $20, de $10, de $5, de $2 et de $1 pour permettre plusieurs possibilités de calcul.

L'équipe devait expliquer la façon choisie pour changer le chèque et ainsi vérifier l'exactitude du calcul.

Tout ce travail permet et d'observer les habitudes de calcul et de déceler les difficultés de chacun dans la manipulation de l'argent.

Voici comme exemple ce qu'on donnait pour un chèque de $358:

3 billets de $100	3 billets de $100	3 billets de $100
5 billets de $10	2 billets de $20	1 billet de $50
8 billets de $1	1 billet de $10	1 billet de $5
	4 billets de $2	3 billets de $1

Pour renforcer le concept du nombre, on peut demander, à ce stade, de reproduire ce montant en utilisant les verres. Ainsi on pourra faire des liens avec ce qui a déjà été vu et remarquer la ressemblance avec la première façon de changer le chèque.

Cet exercice a suscité beaucoup d'intérêt et de réflexions. Dans la pratique la façon de changer leur chèque à la caisse diffère sensiblement. Certains préfèrent avoir des $20 seulement alors que d'autres demanderont des $100 parce qu'il est plus facile d'en vérifier le montant. Le besoin étant ainsi exprimé, on a expérimenté de nouvelles façons de composer les montants d'argent.

Ce travail de manipulation et de calcul devient donc important puisqu'il est directement lié à des situations concrètes.

En général, les personnes ne rencontrent pas trop de problèmes lorsqu'elles choisissent des billets de $100 ou font des regroupements de $100. Elles se heurtent cependant à certaines difficultés lorsque vient le temps de passer à la centaine suivante.

Ainsi à la question suivante: j'ai $280 et j'ajoute $20, combien ai-je? On ne répond pas naturellement $300, mais on regroupera 80 et 20 pour composer un nouveau groupe de 100, lequel s'ajoutera aux 2 autres pour faire 300.

Il ne faut donc pas hésiter et profiter de cet exercice de manipulation pour vérifier, pratiquer et améliorer certains calculs pratiques:

• compter par: $2, $5, $10, $20...
• ajouter des billets: tu as $260, je te donne $5, $10, $100...
• retrancher des billets: tu as $300, tu me donnes $5, $10, $100...
• pratiquer les multiplications:
  3 fois $100, 5 fois $10, 8 fois $2...
• initier à la division dans le sens de regroupement:
  combien de $50 dans $100, $200, $300...
  combien de $20 dans $100, $200, $300...
  combien de $10 dans $100, $200, $300...

Par la suite, chaque personne devait refaire l'exercice mais cette fois, avec le montant de son propre revenu mensuel, et ce, de plusieurs façons différentes.

Exercices

Ajoute des $10 au montant indiqué.
Utilise des billets de $10 pour faire le calcul

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Enlève des $10 au montant indiqué.
Utilise des billets de $10 pour faire le calcul.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Ajoute des $5 au montant indiqué.
Utilise des billets de $5 pour faire le calcul.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Trouve 3 façons de changer ce chèque.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Tu travailles dans une caisse et tu dois changer les montants suivants.
Quels billets donnerais-tu?

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Fais le calcul.
Utilise des billets de $10 pour faire le calcul.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Voici différentes façons de voir un nombre.
Ces exercices vont t'aider dans tes additions et tes soustractions.

89	c'est	80 et 9
89	c'est	70 et 19
89	c'est	60 et 29
89	c'est	50 et 39
89	c'est	40 et 49

Écris le nombre de 3 façons différentes.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

On peut faire la même chose avec les centaines.

248	c'est	200+40+8
248	c'est	100+100 + 20 + 20 + 8
248	c'est	100+100 +10 +10 +10 +10 + 8

Écris le nombre de 2 façons différentes.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

2. Initier au budget

Objectif spécifique2
Initier au budget

Exercice
faire son budget

Matériel
des feuilles du budget, de l'argent de papier, des enveloppes blanches

Organisation
en équipe de 2

Pour initier au budget et au vocabulaire relatif à ce thème, nous avons d'abord travaillé sur un budget type qui reflète de près la réalité d'une personne de l'atelier. Le problème se divise en 3 parties: l'addition des dépenses, la soustraction pour trouver le reste et la division pour chercher la part de chacun. Voici le cas présenté.

Pierre et Marie demeurent ensemble. Ils reçoivent $1160 d'aide sociale par mois. C'est leur revenu.

1. Le loyer est de $280
2. L'électricité est de $68 par mois
3. Le téléphone est de $17.54

Ils ont aussi un compte chez Ameublement Tanguay.
Ils remboursent à chaque mois $35.87

Ce sont leurs dépenses fixes par mois.

Au début du mois, ils prévoient $440 pour l'épicerie et des dépenses diverses.
Marie et son ami se séparent le reste de l'argent pour leurs dépenses personnelles.

De quelle somme disposera Marie pour ses dépenses du mois?

Le budget de Marie et Pierre

[Voir l'image pleine grandeur]

Les dépenses du mois

[Voir l'image pleine grandeur]

Déroulement:

Les personnes travaillent en équipe de 2.

Chaque équipe a un montant d'argent de papier assez élevé avec des $100, des $20, des $10, des $5, des $2, et des $1 pour changer le chèque.

Il faut, dans un premier temps, indiquer les jours du mois choisi sur la feuille blanche du calendrier. Ceci permet de revoir les notions sur le temps et de prendre conscience que le mois compte plus de quatre semaines et qu'il faut planifier en conséquence pour les mois plus longs.

Puis on doit changer le chèque et indiquer les billets reçus sur la feuille du budget.

L'addition

Dans un deuxième temps, on place l'argent des dépenses fixes (loyer, téléphone, électricité, dettes) dans une enveloppe. Cela peut facilement représenter un dépôt à la caisse.

Ici, on apprendra à arrondir les nombres (exemple: si le téléphone coûte $16.75 plus $1 de frais, on peut arrondir à $20). Faire la même chose avec l'électricité à $70 et la dette à $40.

C'est l'étape de l'addition:

• estimer le montant des dépenses et
• pratiquer l'addition en calculant le total des dépenses fixes,
  1- faire le calcul avec l'argent de papier;
  2- faire le même exercice au tableau;
  3- vérifier la réponse avec la calculatrice;
  4- inscrire les montants sur la feuille du budget;
  5- pratiquer l'addition par écrit et avec la calculatrice.

La soustraction

Dans un troisième temps, il faut calculer ce qui reste. Et c'est à l'aide de questions qu'on fera découvrir le sens de la soustraction. Ce sens premier de la soustraction (le reste) est simple et ne cause pas trop de difficultés.

Est-ce qu'il reste plus d'argent ou moins d'argent qu'au départ? Que faut-il faire pour trouver ce qui reste? Quel signe est utilisé pour indiquer "un moins"? Quel nom donne-t-on à cette opération?

On pourra alors

• estimer le montant qui reste,
• et pratiquer la soustraction,
  1- faire le calcul avec l'argent de papier;
  2- faire le même exercice au tableau;
  3- vérifier la réponse avec la calculatrice;
  4- inscrire les montants sur la feuille du budget;
  5- pratiquer la soustraction par écrit et avec la calculatrice..

Plusieurs personnes éprouvent de la difficulté avec la technique de la soustraction. C'est relativement facile d'enlever, de soustraire dans une situation concrète (les dépenses du mois par exemple). Mais l'opération mathématique fait abstraction de cette situation, elle ne porte que sur les nombres. C'est une abstraction difficile à saisir et qui s'explique difficilement par la manipulation alors qu'il n'y a qu'un montant duquel je prends une partie. La difficulté est accrue par le fait que les tables d'addition ne sont pas connues. Chez certaines personnes la difficulté est si grande que nous suggérons d'utiliser la calculatrice.

On peut arriver à démontrer l'opération en travaillant visuellement avec l'enveloppe et l'argent qui reste.

[Voir l'image pleine grandeur]

Prendre l'argent qui reste et l'enveloppe (ne pas mêler) et demander combien il y avait d'argent au départ, puis enlever l'enveloppe pour montrer combien il reste (J'ai $1 160, j'enlève les dépenses $410, il reste $750). Inscrire l'opération au tableau au fur et à mesure.

• Quelle opération faut-il faire pour arriver à ce résultat?
• Comment placerais-tu les chiffres au tableau pour illustrer cette opération?
• Quel signe est utilisé pour cette opération?

Reprendre l'exemple avec les verres mais il reste que la soustraction écrite est une grande source de confusion.

La preuve

Si tu remets l'argent qui reste avec l'argent des dépenses (enveloppe), peux-tu dire combien d'argent il y a en tout? Cet exercice est important puisqu'il permet de comprendre le sens de la soustraction et surtout celui de la preuve.

Il faut refaire plusieurs exercices semblables avec de plus petits chiffres et effectuer parallèlement la soustraction et la preuve au tableau.

Sur le $750 qui reste, il faut maintenant enlever le montant de l'épicerie et refaire les mêmes opérations.

La division: sens partage

La division dans le sens de partage prend tout son sens dans cette 3e étape du problème alors qu'il faut trouver la part de chacun. Chaque équipe devait donc se séparer l'argent qui restait en jouant le rôle de Marie et de Pierre.

Il reste $310. Que faut-il faire pour trouver la part de chacun? Les expressions partager également et séparer moitié-moitié sont utilisées par les participants et les participantes pour expliquer l'opération à effectuer, ce qui permet de constater que le sens de l'opération est connu. Il reste à découvrir comment partager.

Comme chaque équipe avait des billets différents, le partage a donné lieu à toutes sortes d'expérimentations et de questionnements.

Par exemple comment séparer 3 billets de $100 et 1 billet de $10 ou encore 1 billet de $100, 1 billet de $50 et 8 billets de $20

Chez certains, le partage s'est fait à partir du nombre de billets:

2 billets de $100 à l'un, et
1 billet de $100 plus 1 billet de $10 à l'autre.

Il a fallu questionner le partage égalitaire, le moitié-moitié pour comprendre que c'est la somme et non les billets qu'il faut partager.

La décomposition du nombre peut aider à résoudre le problème:
Dans $310, j'ai $300 et $10
Donc chaque personne est assurée d'avoir au moins un $100.
Il faut ensuite changer le $100 qui reste et donner $50 à chacun.
Puis le $10 devient facilement 2 fois $5.

Ce qui fait $100 + $50 + $5 à Marie et $100 + $50 + $5 à Michel.

Pour s'assurer de la compréhension du sens de la division, nous avons poursuivi le problème ainsi: Marie veut s'assurer d'avoir un peu d'argent à chaque semaine du mois. Comment peut-elle répartir son argent pour avoir le même montant à chaque semaine. En calculant la dernière semaine du mois comme une semaine complète, nous aurons 5 semaines.

Le recours aux enveloppes peut faciliter la compréhension et la résolution du problème. En demandant à chaque personne de répartir également l'argent qui reste dans 5 enveloppes, une pour chaque semaine, on reprendra l'idée de la division, du partage d'une quantité en plusieurs petites parties égales.

L'utilisation de la calculatrice

Il n'était pas question d'introduire à cette étape l'algorithme de la division. Cependant, les personnes de l'atelier étaient curieuses de savoir comment se fait cette opération sur la calculatrice. Puisque cet outil leur permet désormais d'effectuer des calculs qu'elles ne pourraient que difficilement exécuter autrement, la calculatrice prend une place importante dans l'atelier et dans leur vie. Nous permettrons et même encouragerons ceux et celles qui ont plus de "misère" avec le calcul à se servir de cet instrument, à en comprendre le fonctionnement mais seulement après s'être assuré que le sens de l'opération est bien compris.

En reprenant le problème du $310 à séparer "moitié-moitié", nous tâcherons d'aller encore plus loin dans l'explication du sens de la division en demandant aux personnes de verbaliser ce qu'elles font.

• Que faut-il faire pour séparer moitié-moitié? Il faut diviser.
• Que faut-il diviser? Les $310.
• En combien de parties faut-il les diviser? En deux.

Nous introduisons le signe de la division que nous retrouvons sur la calculatrice en revoyant chacun des signes déjà appris.

Et nous reprenons l'opération étape par étape:
j'inscris le montant à diviser: 310,
j'indique l'opération à effectuer -:-,
j'indique ensuite en combien de parties il faut diviser: 2
je demande la réponse =

Il ne faut pas s'arrêter à cette étape puisque la compréhension de la division, du partage, réside essentiellement dans la réponse. Il faut s'assurer que les personnes réalisent que le résultat signifie qu'on a $155 pour la part de Marie et $155 pour Michel.

Nous retrouvons ici la division dans son sens de partage (par opposition à celui de regroupement ou de mesure comme par exemple: combien de 5 dans 25). Ce sens spécifique constitue la principale difficulté de la compréhension de cette opération.

Après avoir travaillé sur ce budget type, nous avons proposé au groupe de travailler à partir de leurs propres revenus et dépenses. Dans l'ensemble, les personnes ont assez bien répondu à la proposition. Nous avons profité d'un début de mois pour distribuer les feuilles du budget en demandant d'y inscrire le montant de leur chèque (toutes les personnes de l'atelier reçoivent des prestations d'aide sociale) et d'y indiquer les dépôts faits à la caisse et les billets qu'elles avaient reçus. Elles devaient aussi indiquer le montant des dépenses fixes. Ainsi les gens pouvaient calculer combien il leur restait pour les autres dépenses (nourriture) et estimer combien d'argent ils pourraient avoir pour chaque semaine du mois.

Exercices

Mon budget

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Les dépenses du mois

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Mes dépenses du mois de...

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Pratique-toi à calculer les dépenses.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Calcule le reste

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Nous avons poursuivi le travail de manipulation de l'argent avec un petit exercice rigolo. L'exercice peut se faire en groupe ou deux par deux. Il s'agissait de payer des achats fictifs. Ce travail a permis de voir comment les gens fonctionnent avec l'argent.

Quels billets prendrais-tu pour payer un achat de:

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Les gens ont d'abord donné le montant exact. Ceci est un bon exercice de calcul.

Puis nous avons demandé de ne pas utiliser de billets de $5, $2 et $1 pour voir comment les gens allaient "arrondir".

Afin de pratiquer le calcul de l'argent, nous leur avons demandé de donner une sorte de billet seulement: des billets de $2 et de $5 pour les petits montants, des billets de $10, $20 ou $50 pour les montants plus élevés.

Le change

À partir de cet exercice, nous avons aussi travaillé la notion du change. En illustrant côte à côte le coût de l'article et le change, on permet de visualiser la décomposition du paiement initial en deux parties: le prix de l'article et ce qui me revient: $20 , c'est $17 et $3.

3. Comprendre le rôle et le sens du point

Objectif spécifique 3
Comprendre le rôle et le sens du point

Exercice
payer ses achats

Matériel
argent en billets et en monnaie

Fonctionnement
en groupe

L'exercice suivant, semblable au précédent, peut se faire à partir de d'articles d'épicerie. Il vise à pratiquer la lecture des montants d'argent comprenant des "cennes", à comprendre le rôle du point, à "arrondir" et à estimer les coûts.

Quels billets prendrais-tu pour payer ces achats?

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

En général, la lecture des montants d'argent ne cause pas trop de problème. Lorsqu'on a compris que le point sépare les dollars des "cennes", la seule difficulté réside dans la lecture des nombres, surtout les 70 - 80 - 90.

Ce travail doit permettre d'expliquer les choix posés. Ainsi, pour un achat de $2.89, une personne peut payer avec $3, et une autre avec $5. La discussion doit amener les gens à réaliser qu'il faut, pour évaluer les coûts de plusieurs articles, rester le plus près possible du coût d'achat.

Ici encore, on travaillera avec la notion du change. Par exemple, on fera décomposer le $3 et le $5 en pièces de $1. De cette façon, les gens peuvent "voir" le change sur $3 et sur $5

Création de matériel par les gens de l'atelier

Matériel
circulaires d'épicerie ou de pharmacie, cartons de 4 par 6 po, ciseaux, colle, crayons feutres

Fonctionnement
en équipe de deux ou 3 personnes

Chaque équipe doit préparer 9 cartons sur lesquels seront collés des articles découpés dans les circulaires.

Les coûts devront correspondre aux montants arrondis de $1 à $9 inscrits à l'endos des cartons (ex.: le premier carton pourrait avoir une publicité de boîte de soupe à 89¢ d'un côté et le montant $1 inscrit de l'autre; sur le dernier carton, il faudrait ainsi prendre plusieurs livres de viande pour atteindre le montant de $9).

Quand tous les cartons sont prêts, on peut les classer par catégories sur les tables et idéalement faire deux groupes pour éviter la cohue dans la suite de l'exercice qui peut se faire en grand groupe, en équipe de 2 ou individuellement.

Ainsi, on pourra:

1. choisir plusieurs articles et estimer le coût de l'épicerie;.
2. fixer un certain montant par exemple $30 et ne pas le dépasser;.
3. fixer un certain montant et arriver juste;.
4. dépasser le montant fixé et enlever un article.

Dans un premier temps, on calculera en utilisant les cartons du côté du prix arrondi ce qui en fait un bon exercice de calcul mental.

Il faut encourager à regrouper par dix et par paires qui sont plus faciles et déjà connus pour la plupart.

En déplaçant les cartons suivants: $4 - $8 - $6 - $9 - $2 - $5 - $1, on aura $4 et $6, $8 et $2, $9 et $1, et $5 pour $35.

Lorsque les gens ont bien intégré la notion d'arrondir, ils travailleront avec les cartons du côté du produit.

Ce matériel peut-être utilisé régulièrement, en début d'atelier, pour développer des automatismes.

Commentaires généraux pour conclure

La question de l'argent s'avère une préoccupation essentielle chez les personnes qui participent aux ateliers de calcul. C'est pourquoi nous avons mis l'accent sur la manipulation de billets de banque durant ce thème.

Le calcul de l'argent suppose la connaissance de plusieurs notions dont la connaissance du nombre et de la numération, ainsi que celle de l'addition et du calcul par 2, 5, 10 et 20. Ces rudiments de calcul ont été repris à l'intérieur de situations concrètes avec, cette fois, le modèle de l'argent.

Les personnes ont développé certaines aptitudes en calcul par le biais des thèmes précédents et dans leurs activités quotidiennes. Cependant ces aptitudes sont limitées et le support de matériel concret demeure encore indispensable. La manipulation devient donc une occasion pour corriger ou améliorer certains calculs. Ainsi, dans l'atelier, une personne reproduisait toujours la même erreur dans le calcul par cinq; elle avait développé un automatisme qu'il fallait corriger. Cette personne comptait bien par cinq jusqu'à trente mais après, elle continuait par dix ce qui donnait: 5, 10, 15, 20, 25, 30, 40, 50...

La manipulation de l'argent nous a permis de comprendre d'où provenait son erreur. En comptant son argent, cette personne regroupait ses billets de cinq dollars par groupe de deux et comptait plutôt par dix. Avec des exercices appropriés, le retour sur le calcul des minutes et surtout la prise de conscience de sa façon de calculer, cette personne a pu modifier son automatisme.

Les exercices développés durant ce thème visent à atteindre deux objectifs: l'exactitude et la rapidité. Durant les exercices de manipulation de l'argent, nous avons constaté les difficultés rencontrées par les personnes dans leur vie quotidienne. Il leur faut du temps et de la concentration pour calculer et s'assurer de l'exactitude de leur calcul. Lorsqu'elles font des opérations financières, la rapidité de calcul des préposés aux caisses laisse bien peu de temps aux personnes pour vérifier leur retrait. Il se crée alors un sentiment d'inquiétude. Comment être sûr que l'argent qu'elles reçoivent correspond au montant exact? C'est pourquoi certaines personnes ne demanderont que des billets de $100, d'autres se fieront totalement au caissier ou encore referont maintes fois le calcul avec toujours ce sentiment d'incertitude et d'erreur.

Nous avons par exemple travaillé davantage le calcul par 20 avec un participant. Celui-ci, après avoir déposé le montant des dépenses fixes, retirait la balance de son chèque en billets de $20 seulement. En établissant d'avance le montant à retirer, il pouvait ainsi calculer le nombre de billets de $20 qu'il devait recevoir. Cette façon de faire lui permettait de compter en même temps que le caissier et lui procurait un sentiment de sécurité.

Ainsi le travail avec les chèques et le budget permet de développer des habitudes de calcul, de prévoir d'avance le montant exact à percevoir à la caisse, de savoir combien d'argent ils ou elles disposent après avoir payé les dépenses fixes du mois. Il faut donc les encourager à travailler à partir de leur situation personnelle et répéter souvent et de différentes façons ces exercices de manipulation.

Le travail avec la calculatrice

Plusieurs personnes de l'atelier compte sur leurs doigts. C'est une habitude depuis longtemps développée et que nous avons plutôt encouragée. Et c'est bien ainsi lorsqu'il s'agit de nombres inférieurs à dix. Par exemple 8 et 6, cela se compte bien sur les doigts. Cependant, dans les chiffres plus élevés telles les dépenses du mois, ce n'est plus possible. C'est alors qu'on aura recours à la calculatrice.

Le travail avec la calculatrice doit se faire en même temps que la manipulation. Si on sait bien s'en servir, celle-ci devient un outil de plus dans l'apprentissage. Mis en parallèle avec la manipulation, le travail sur la calculatrice permet de verbaliser, de définir le sens, de nommer et d'identifier les termes de l'opération.

Lorsque les personnes sont capables, dans la soustraction $1160 - $410 = $750 d'expliquer et d'identifier chacun des termes et des signes de l'opération, elles ont accompli un grand pas dans la compréhension. Et que dire si elles peuvent expliquer et revenir au point de départ (1160) à partir du résultat 750.

Il ne s'agit pas de donner aux gens une suite de chiffres à entrer sur la calculatrice mais bien de leur faire comprendre la logique et le maniement de cet instrument. Ainsi une personne de l'atelier voulait vérifier sur la calculatrice la manipulation du $310 séparé moitié-moitié. Incapable d'associer l'idée de partage à la division, elle restait bloquée devant l'opération à effectuer. Comment faire moitié-moitié sur la calculatrice? C'est en lui demandant de séparer une feuille moitié-moitié que cette personne a trouvé qu'il fallait diviser en deux. Ainsi le sens et la compréhension de l'opération sont développés alors que la technique de l'opération, parfois difficile, peut se faire facilement sur la calculatrice.

Bien sûr, ce module sur le budget n'a pas dans les faits changer les conditions de vie des participants et des participantes. Cependant, après avoir travaillé sur le budget, une personne a diminué ses dépenses de téléphone, très élevées par rapport à ses revenus. Nous pensons que le travail sur les dépenses du mois, lorsque les gens se sentent en confiance, peut amener certaines prises de conscience concernant la manière de dépenser en début de mois, les dépenses et les problèmes liés à l'alcool, le coût du loyer et la façon de se loger: HLM, coopérative, etc.

Module 4 – Le groupe d'achat

Groupe: n. m. ( it. groppo, nœud ). Ensemble de personnes ou de choses réunies dans un même endroit: un groupe de curieux. // Ensemble de personnes qui ont des attitudes et des comportements communs, avant un objectif commun qui conditionne la cohésion de ses membres : un groupe politique, un groupe de travail.

Achat: n. m. Action d'acheter. //

[Voir l'image pleine grandeur]

Présentation du projet

Expérimentation d'un projet de création d'un groupe d'achat

Pourquoi organiser un groupe d'achat.

L'épicerie constitue, avec les frais du loyer, les principales dépenses inscrites au budget des gens de nos ateliers. Les frais de loyer étant la plupart du temps incompressibles, c'est donc du côté de l'épicerie qu'on peut penser trouver des solutions permettant de joindre les deux bouts. Il faut donc essayer de s'organiser le mieux possible afin de profiter au maximum des spéciaux offerts à chaque semaine dans les épiceries. Les magasins à grande surface offrent, si on sait bien calculer et vérifier, des spéciaux qui en valent la peine.

Mais pour bénéficier de ces économies, il faut être capable de lire les circulaires, de comparer les prix en vigueur et d'acheter quand le spécial se présente. Souvent le budget est tellement serré qu'il faut limiter les achats aux besoins immédiats. De plus, en vivant seul-e, il n'est pas toujours rentable d'acheter en grande quantité. Enfin les personnes qui n'ont pas d'auto sont limitées aux épiceries du quartier et ne peuvent profiter des spéciaux qu'offrent les épiceries à grande surface.

L'idée d'organiser un groupe d'achat a été présentée comme projet d'atelier de calcul, projet que nous voulions expérimenter à petite échelle d'abord. C'est seulement après cette expérience que nous serons en mesure d'évaluer la possibilité et la pertinence de créer un groupe d'achat qui fonctionnerait de façon régulière et qui comporterait des avantages réels tant sur le plan économique que sur le plan des apprentissages mathématiques.

Les notions mathématiques présentées dans ce projet ont l'avantage d'être étudiées à l'intérieur de situations d'apprentissage issues de la vie courante. Les problèmes proposés sont connectés au quotidien donc réels et concrets. L'apprentissage devient fonctionnel, pratique, global; les connaissances acquises ont ainsi une portée d'utilisation immédiate.

Il suffit de penser à toutes les activités nécessaires à la mise sur pied de ce groupe d'achat. En premier lieu, il faut se familiariser avec la façon d'écrire et de lire les montants d'argent, d'entrer les données sur la calculatrice, de savoir quand et comment utiliser le point. Mais aussi, il faudra pour acheter et revendre, peser, mesurer, évaluer, comparer les prix et les produits, calculer les taxes, etc.

Voici une liste des notions et des apprentissages qu'il est possible d'exploiter à travers un tel projet:

• les 4 opérations mathématiques
• la règle de trois,
• l'estimation,
• le gramme, le kilogramme, l'once et la livre,
• les millilitres et le litre,
• la tasse à mesurer,
• la demie, le quart et le tiers,
• les taxes,
• l'argent et... la calculatrice.

Des outils sont essentiels pour rendre l'apprentissage vivant et concret:

• la balance en grammes et en kilos,
• la balance en onces et en livres
• les contenants en grammes et en kilos,
• les contenants en millilitre et en litre,
• le contenant de 4 litres,
• les tasses à mesurer,
• l'argent et la caisse enregistreuse ou une calculatrice à ruban et une petite caisse.

Dans les pages qui suivent, on reprend étape par étape le cheminement que nous avons suivi tout au cours des ateliers.

Préciser les besoins

• Comment je fais mes achats$
• Où je fais mes achats?
• Quelle est la meilleure place pour acheter:
  - la nourriture?
  - les produits de toilette?
  - les produits de nettoyage?

Pour les résidants du quartier qui n'ont pas d'auto, il y a deux endroits pour faire l'épicerie: à l'Inter Marché et chez Daniel. Chez ce dernier, la publicité se fait de bouche à oreille; il n'existe aucun circulaire pour annoncer les prix. Nous sommes allées chez ce marchand pour faire une liste de prix des produits courants. Et nous avons utilisé les circulaires de l'Inter Marché.

Il y a dans le quartier une pharmacie qui offre de bons spéciaux et, là encore, c'est surtout de personne à personne que l'information se transmet.

Évaluer les coûts

• Est-ce que je regarde les formulaires?
• Est-ce que je surveille les spéciaux?
• Est-ce que je connais le coût des produits que j'achète?
• Est-ce que je peux reconnaître les articles offerts dans les circulaires?

La difficulté à lire pour une part, et l'habitude acquise d'aller au même endroit d'autre part, font que plusieurs personnes de l'atelier consultent peu ou pas les circulaires. On fait en général une grosse commande au début du mois et on essaie de s'organiser du mieux qu'on peut pour terminer le mois (le recours aux banques de nourriture est souvent la seule façon de s'en sortir).

Une caisse enregistreuse pour apprendre...

Nous avons constaté qu'il n'est pas toujours facile, pour les personnes en début d'apprentissage, d'utiliser les circulaires pour faire l'épicerie. Il y a, dans ces dépliants, maintes notions qui doivent être expliquées et comprises avant de pouvoir s'en servir adéquatement.

Lire, écrire et comparer des nombres décimaux (argent) Premièrement, nous avons dû nous assurer que les personnes étaient capables de lire, d'écrire et de comparer des montants d'argent. Nous avons, à cet effet, prévu un exercice qui permettrait de déceler les difficultés puis de pratiquer la lecture et l'écriture des montants d'argent. Pour rendre l'exercice vivant et concret, nous avons apporté des articles d'épicerie sur lesquels les prix étaient indiqués.

Le travail s'est effectué sur la caisse enregistreuse, avec de l'argent de papier et de la monnaie. Les gens pouvaient aussi travailler avec la calculatrice.

Les objectifs d'apprentissage :

• Lire des montants d'argent
• Écrire des montants d'argent
• Arrondir des montants d'argent
• Estimer des coûts et additionner dans sa tête
• Estimer son change et le compter
• Apprendre à se servir de la calculatrice

Une personne choisit pour commencer 3 ou 4 produits. Elle doit estimer le coût de ses achats.

Pour cela, il faut arrondir les prix.:
$1.79, c'est proche de quoi?
avec quel billet pourrais-tu payer?

On peut regrouper 2 articles pour plus de précision.
Un article à $3.29 et un article à 59¢
Est-ce que tu as assez de $4.00 pour payer ces deux articles?

Pour terminer il faut payer et estimer combien il lui reviendra d'argent. Cette simulation permet de voir comment les gens se débrouillent pour payer leurs achats.

Estimer et compter le change

Estimer et calculer le change constitue une des plus grandes difficultés rencontrées par les personnes avec qui nous travaillons. Cette opération exige un grand nombre de connaissances plus ou moins complexes. La compréhension satisfaisante de la numération et de l'addition, la facilité à compter par 5, par 10 et par 25 et l'identification des différentes pièces de monnaie sont des rudiments indispensables à cette activité. La capacité de faire abstraction et la mémorisation entrent aussi en jeu pour la réalisation de ce calcul.

Devant ce fait, nous avons d'abord insister sur le calcul des piastres seulement. J'ai un achat de $3.59 et je paie avec un $5.00. Est-ce qu'il va me revenir juste de la monnaie ou s'il va me revenir des piastres? Combien de piastres? Insister pour que la personne explique sa démarche de calcul. "Il devrait revenir au moins $1.00 et de la monnaie parce que ça va me prendre 3 piastres et une autre piastre pour le 59 cents".

La suite de l'exercice se fait sur la caisse enregistreuse. Une deuxième personne enregistre les achats sur la caisse.

Elle dit et marque le prix des articles.
Elle fait le total et compare avec l'estimation.
Elle remet le change à sa "cliente" qui doit le vérifier.

Travailler avec la caisse enregistreuse a rendu cet exercice extrêmement vivant et enrichissant. Toutes les personnes étaient motivées à apprendre et à utiliser la caisse. Elles ont, en plus des apprentissages réalisés, constaté l'importance de surveiller et de vérifier les prix indiqués à la caisse lorsqu'elles font leur épicerie.

Pendant que les deux personnes travaillent sur la caisse, le groupe peut faire les mêmes opérations sur la calculatrice.

L'écriture des montants d'argent et l'entrée des données sur la calculatrice causent des difficultés. Il faut pratiquer et expliquer comment le faire.

L'addition avec des points

Saurais-tu faire cette addition?
39¢ + 4¢ + $7 + $15 + 89¢

Pour montrer la différence entre la lecture et l'écriture des montants d'argent, on peut travailler avec des sous noirs, des dix sous et des piastres et expliquer le rôle du zéro.

0.39 + 0.04 + $7.00 + $15.00 + 0.89

Il faut aussi apprendre aux gens à évaluer approximativement la réponse. En sachant que le total sera autour de 20$, on peut déceler les erreurs.

Mettre les chiffres en colonne.

[Voir l'image pleine grandeur]

Avec ta calculatrice

Quelle différence entre écrire 1¢ et 10¢

Additionne ces montants d'argent avec ta calculatrice.

[Voir l'image pleine grandeur]

Des balances... c'est indispensable

Les objectifs:
mesurer les poids et le volume initier à la notion de différence additionner et soustraire introduire la demie et le quart

Apprendre à utiliser la balance en kilos et en livres Pour pouvoir comparer les prix des circulaires, il faut connaître la livre, le kilo, le gramme, le litre et le millilitre Il faut aussi être en mesure de reconnaître tous les symboles (kg, g, l, ml, lb) utilisés pour indiquer ces quantités.

Comparer le prix au kilo et à la livre ou comparer 250 g et 750 g n'est possible que si on a pu faire l'expérience de peser et de manipuler, à de nombreuses reprises, des poids de toutes sortes. Les personnes qui ont appris les livres et les onces ont beaucoup de difficultés à saisir que le kilo est une autre unité de grandeur. Elles croient que les produits vendus au kilo sont plus dispendieux que ceux vendus à la livre.

Il nous apparaissait donc indispensable de se procurer des balances pour expliquer ces deux unités de mesure. De plus, il semblait évident qu'il fallait une balance en livres et une autre en kilos si on voulait faire saisir l'idée que le kilo et la livre sont des conventions établies et qu'il faut utiliser soit l'une, soit l'autre.

En plus des balances, nous avons utilisé des contenants de différentes grandeurs et un produit à peser, du riz en l'occurrence. Il s'agissait surtout, dans un premier temps, d'apprendre à manipuler ces outils d'en faire une lecture appropriée.

Démarche d'un atelier

Nous avons séparé le groupe en deux. Une partie du groupe travaillait sur la balance en livres alors que l'autre se familiarisait avec la balance en kilos. Les gens devaient peser des objets autour d'eux: dictionnaires, crayons, porte-clés, sacs d'école, bouteilles de liqueur, etc. Cette première approche est amusante et permet de vérifier les connaissances des mesures de poids chez les participants et participantes. Elle permet aussi au groupe d'évaluer, de soupeser des poids lourds et des poids légers, d'évaluer le poids de 2 articles, de comparer les kilos et les grammes, d'introduire les fractions, le quart et la demi-livre. Nous avons donné le temps à chaque groupe d'expérimenter le fonctionnement des deux balances.

Puis, avec les contenants de différentes grandeurs, nous avons commencé à peser du riz. Nous nous sommes servi des contenants de 175g, 250g, 300g, 454g, 500g et 1 kilo. Il a fallu d'abord identifier ces contenants et leur capacité. Nous avons ensuite pesé et comparé les contenants de 250 g, 500 g et 1 kilo pour établir des formules. Ça prend 2 fois 250 g pour faire 500 grammes. Deux fois 500 g font un kilo ou 1000 grammes.

J'ai 1 kilo de riz que je veux vider dans des contenants de 250 g. Combien de contenants me faut-il? La manipulation et l'expérimentation prennent ici tout leur sens Remplir et peser les contenants pour arriver au kilo répond à la question.

Nous avons ensuite pesé ces quantités sur la balance en livres pour établir des comparaisons:

• le kilo fait un peu plus de 2 livres;
• les 500 g font environ 1 livre;
• les 250 g font environ une demi-livre.

Objectif
Comparer les prix.

Exercice
Faire une petite épicerie de $20

Matériel
Des circulaires

Fonctionnement
En équipe de deux.

À l'aide des circulaires de l'Inter Marché et de la liste des prix de Chez Daniel que nous avons illustrées, nous avons demandé au groupe de faire une petite épicerie d'environ $20 en comparant les prix des marchands.

Pour les plus avancés, nous avions prévu des quantités différentes comme par exemple les contenants de margarine de 2 livres et de 3 livres, ce qui a donné lieu a un bel exercice de calcul. En utilisant des contenants d'une livre, nous avons démontré la nécessité de savoir le prix d'une livre pour comparer les prix.

Les personnes devaient évaluer le coût de leurs achats et ne pas dépasser $20.

Pour les gens qui ont très peu d'habileté en lecture, la recherche dans les circulaires est très difficile. Il aurait été préférable de faire d'abord une liste d'épicerie pour aller ensuite vérifier les prix dans les deux circulaires. Laisser à eux-mêmes, les équipes choisissaient quelques articles pour arriver à $20.

Cependant cet exercice a permis de vérifier les habitudes alimentaires des participants et des participantes, de comprendre les difficultés rencontrées dans l'utilisation des circulaires et de déceler les connaissances qu'ils et elles ont des prix des produits fréquemment achetés.

[Voir l'image pleine grandeur]

Comme l'exercice précédent a été difficile, nous avons repris le travail d'une autre façon.

Sur une même feuille, nous avons illustré au centre de la page des produits d'épicerie des 2 marchands et inscrit le prix de chaque côté. La lecture des prix se fait mieux ainsi et la comparaison est plus facile.

Quelques personnes ont de la difficulté à comparer certains prix et à trouver celui qui est le moins élevé comme par exemple 69C et 79c et $3.49 et $2.89.

1. La difficulté de comparer des montants d'argent provient: du double problème de la formulation verbale et de la représentation écrite des nombres (69¢ et 79¢),
2. de la perception des nombres décimaux comme s'ils étaient séparés. D'ailleurs, la façon de dire ces nombres (2 piastres et 89 cennes), renforce cette perception. On sent ici combien il est important de connaître la valeur des nombres et le rôle du point pour pouvoir comparer.

Nous avons travaillé sur cette difficulté de comparaison en revenant sur la valeur des nombres à l'aide de sous noirs, de dix sous, et de piastres.

Comparer les prix 69 ¢ et 79 ¢:
En plaçant côte à côte l'argent (les 10 sous et les sous noirs) représentant les deux montants, on peut observer le 60 et 19, le 60 et 9, comparer l'écriture du nombre avec le nombre de pièces de monnaie et "voir" la différence de prix.

Qu'est-ce qui coûte le moins cher?
"C'est celui pour lequel je donne le moins d'argent."
Combien de moins? "10¢ de moins"

Nous avons fait de même pour $3.49 et $2.89.

Pour comparer et "voir" la différence, les gens devaient utiliser des dix sous comme illustré:

1 $

1 $

10¢

10¢

10¢

10¢

10¢

l0¢

10¢

10¢

10¢

10¢

10¢

10¢

10¢

l0¢

9¢

1 $

1 $

10¢

10¢

10¢

10¢

10¢

10¢

10¢

9¢

Après avoir constaté de visu la différence, un participant a voulu savoir comment s'y prendre pour trouver cette différence avec la calculatrice.

Voici l'exemple du cheminement qu'il a fallu faire pour découvrir la solution au problème: quelle opération mathématique permet de trouver la différence.

Durant l'expérimentation, nous avons toujours favorisé la découverte de la solution par les participants et les participantes plutôt que de donner des réponses toutes faites. Voici la description des essais et des réflexions de cette recherche de solution. Nous avons choisi le prix du maïs en grains à 63c et 65c, en disposant les sous sur la table. En partant les gens savaient que la différence est de 20.

Les solutions des participant-e-s sont en caractères gras.

Quelle opération faut-il faire pour trouver la différence?
Il faut diviser,

qu'est-ce qu'on divise?
On divise 63¢,

qu'est ce que ça veut dire diviser?
Ça veut dire séparer,

comment on va séparer?
On va séparer en deux,

ok séparez les 63¢ en deux.
Ça donne 31¢ et 31¢ et il reste une cenne. Il faudrait séparer la cenne en deux.

Est-ce que ça donne la différence?
Non... Il faut multiplier.

Qu'est-ce que vous allez multiplier?
63¢ par deux.

Tout de suite les gens se rendent compte que ça ne marche pas. Reprenons du début: pour trouver la différence, il faut comparer deux choses, deux quantités, deux grandeurs. Je me suis donc comparée avec une participante. Nous nous plaçons côte à côte.

Il y a une différence de grandeur entre nous deux. Est-ce qu'il faut nous multiplier, nous diviser pour trouver la différence?
Non.

C'est quoi la différence entre nous deux.
C'est une tête. Il faudrait te couper la tête.

Alors que faut-il faire pour trouver la différence?
Qu'est-ce qu'on fait quand on coupe, quand on enlève un bout? Il faut soustraire.

Qu'est-ce qu'il faut soustraire?
65¢ moins 2¢ ça donne 63¢

Mais comme on voit que la différence est 2, on se rend compte qu'on se trompe quelque part dans l'opération.

Alors un participant se lève, prend les 2 cennes et dit c'est ça la différence, c'est 2 cennes. (Démontrer par le calcul ce qui est évident lui semblait absurde et inutile.)

Oui c'est ça la différence, c'est ce qu'il y a en plus ou en moins selon ce qu'on regarde, mais pourrais-tu faire la même chose avec $2.09 et $1.78? Comme la différence est plus difficile à calculer dans cet exemple, il faut donc trouver l'opération qui nous donnera la réponse.

Nous reprenons l'illustration des 2 montants avec des pièces de monnaie. (Ne prendre qu'un dollar et des 10 sous pour faire $2.09 afin de faciliter la comparaison.) En comparant, on trouve que la différence est 31¢.

Maintenant est-ce qu'on peut le faire sans les sous?
Oui, j'ajoute 1¢ à $1.78.

Ensuite?
J'ajoute des 10¢, jusqu'à $2.09

Qu'est-ce que ça fait?
Les gens ont saisi le principe de compléter, mais la difficulté réside dans le calcul mental à effectuer, dans un manque de pratique du calcul de l'argent.

C'est au moment où le groupe effectuait le calcul qu'un participant a fait le lien avec les chiffres utilisés et trouvé qu'il pouvait soustraire $1.78 de $2.09, pour arriver à la même réponse.

En faisant le calcul avec la calculatrice, des personnes ont d'abord inscrit le petit montant soit:
1.78 - 2.09 = Minus 31 ou -31.
Cette façon de faire est possible dans ce cas et répond au sens du raisonnement. Le - 31 indique ce qui manque pour faire 2.09. Cependant, nous leur faisons remarquer qu'il est préférable de placer le gros chiffre en premier.

Même si les gens travaillaient avec la calculatrice, nous refaisions toujours le calcul au tableau en expliquant la technique de l'opération.

Nous avons continué l'exercice en demandant au groupe de trouver la différence de prix pour les autres articles d'épicerie.

Comparer les prix de quantités différentes

Objectif
Comprendre qu'on ne peut comparer les prix que pour des quantités équivalentes et trouver comment ramener 2 quantités différentes à des quantités semblables.

Matériel
un sac de 2 kg et un sac de 4 kg de sucre.

Poser le problème et laisser discuter.

Quel est le meilleur achat? 2 kilos à $1.89 ou 4 kilos à $3.38? Poser les sacs sur la table et susciter la discussion. Qu'est ce qui coûte le moins cher, le gros sac ou le petit?
C'est $1.89

Oui c'est moins cher, mais est-ce qu'on a la même quantité?
Non, on en a plus dans le gros sac, c'est pour ça que ça coûte plus cher.

Que faudrait-il faire pour pouvoir comparer les prix?
Il faut avoir la même quantité. Ça prendrait 2 sacs de 2 kilos pour faire 4 kilos.

En effet, pour comparer les prix, il faut d'abord trouver comment arriver à la même quantité, c'est important. Il faut trouver le prix pour des quantités pareilles.

Qu'est ce qui est plus cher: 2 sacs à $1.89 ou 1 sac à $3.38?

Est-ce qu'on peut estimer à peu de cennes près ce que fait 2 fois
$1.89? $1.89 c'est proche de quoi?

De $1.90, de $2.00, il manque 11 cennes pour faire $2.

Alors pour mes 2 sacs de 2 kilos, je paierai à peu près quoi?
$4.00

Quel est le prix exact?
On peut faire 1.89 + 1.89.
On peut faire aussi 2 x 1.89

On apprend à faire ces opérations sur la calculatrice mais aussi par écrit pour pratiquer l'addition avec retenue et la multiplication.

Le travail avec les sacs de sucre a provoqué d'autres questions et d'autres constatations: c'est quoi 2 kilos et 4 kilos en livres? Nous avons donc pesé les 2 sacs et donné le poids en livres: le 2 kilos correspond à environ 4 1/2 livres et le 4 kilos équivaut à environ 9 livres.

Nous avons profité de l'exercice pour faire un retour sur les fractions et même pratiquer oralement l'addition de fractions en faisant 4 et demi plus 4 et demi et constaté que 4 1/2, c'est la moitié de 9.

Bien que n'ayant pas encore travaillé avec des nombres fractionnaires, il n'y a eu aucune difficulté à résoudre ces équations. Profitant de la situation, nous revoyons la demie et faisons des liens avec la demi-heure, la demi-livre, le demi-pouce, la demi-tasse et retenons que dans tous les cas, 1/2 + 1/2 = 1.

Toute cette manipulation a soulevé un autre questionnement: est-ce qu'on peut dire que le sac de 2 kilos est la moitié du sac de 4 kilos. Pour certaines personnes c'était évident puisque la moitié de 4 est 2, mais l'évidence n'a pas fait unanimité. Une personne ne croyait pas que le sac de 4 kilos pouvait contenir 2 sacs de 2 kilos. Ceci a fourni une belle occasion d'amorcer une réflexion sur le volume et d'introduire les notions de hauteur, d'épaisseur et de largeur en comparant les 2 sacs.

Par cette discussion et cette réflexion le groupe a pris conscience qu'il n'est pas nécessaire de doubler toutes les dimensions du sac pour doubler sa capacité.

Il a fallu faire l'expérience concrètement (vider le sac de 4 kilos pour le remplir ensuite avec 2 sacs de 2 kilos) pour réaliser que effectivement le sac de 4 kilos contenait 2 sacs de 2 kilos.

Nous présentons à titre d'exemple le cas d'un problème où des données incomplètes peuvent conduire à une mauvaise piste dans la recherche de solution.

Le problème a été soulevé ainsi: quel est le meilleur endroit pour acheter la bière?
Un participant nous dit qu'il payait $27 pour la caisse de 24.
Un autre affirme qu'il payait $11 pour la caisse de 12.

Un troisième dit qu'il achetait seulement des cartons de 6 bières mais ne se souvenait pas du prix.

Cette donnée a mêlé tout le groupe. Alors que la question de départ consistait à rechercher le meilleur prix, le groupe s'est plutôt attardé à chercher le prix de 6 bières à partir des données existantes. D'où l'importance de garder en tête la question de départ et d'avoir en main toutes les données pour résoudre un problème.

Malgré tout, nous avons travaillé ce problème sous différents aspects en profitant de la situation pour revoir des notions déjà vues:

• la multiplication par 12 ou compter par 12;
• la moitié ou la demi de 6, 12, 24;
• la division avec la question: si vous payez la caisse à deux, combien chacun va-t-il payer?

27 divisé en deux
Exposé de la méthode de division d'un participant

[Voir l'image pleine grandeur]

• le calcul par 10, en calculant le prix des bouteilles vides;
• la multiplication par 10: 6 fois 10¢, 8 fois 10¢, 12 fois 10¢, etc.

En fin de compte, ce que nous retenons de cette situation, c'est que chaque problème peut facilement devenir un sujet d'expérimentation et d'apprentissage varié s'il est bien exploité.

Des patates au kilo ou à la livre

Objectif
Reconnaître le kilo et pouvoir faire des comparaisons avec la livre. Comprendre que ce sont deux unités de grandeur différentes.

Pour introduire la notion de kilo, nous avons acheté un sac de 50 livres de patates. Ce choix se justifie pour deux raisons. C'est un produit qu'on achète régulièrement (contrairement au riz qui avait été utilisé dans l'expérimentation de la balance), et on reconnaît assez facilement les quantités de 5, 10, 20, et 50 livres. De plus, à la différence du riz, il est facile de voir, de compter les patates pour faire une livre et un kilo. Ainsi on verra facilement par le nombre de patates que le kilo est un peu plus que deux livres.

Démarche

Voici un sac de patates. Il a coûté $3.59.

La discussion a donné lieu à un échange sur le prix et la quantité. Les gens ont fait des comparaisons avec le prix payé pour de plus petites quantités et évalué combien de sacs de 5 livres et de 10 livres on pouvait faire avec ce 50 livres.

Le poids étant indiqué de deux façons sur le sac, on constate que malgré cette différence, ces deux poids représentent la même quantité de pommes de terre.

50 livres et 22.7 kg c'est la même chose. La décimale cause ici un problème et ne pourra être expliquée qu'après avoir exploré le kilo.

Pour "voir" et comprendre ce que représentent un kilo et une livre, il faut peser et comparer. Nous avons décidé de faire des petits sacs de 1 livre et de 1 kilo.

Le groupe s'est divisé en deux et chacun a pesé sa livre et son kilo de pommes de terre. Ainsi, la comparaison est possible: pour une livre j'ai 3 patates et pour un kilo, 6 ou 7 patates de grosseur semblable. Les gens sont alors en mesure de "constater" qu'un kilo correspond à un peu plus de 2 livres.

L'exercice s'est continué en faisant des sacs de poids différents en livres et en kilos afin de se familiariser davantage avec les kilos, les grammes, le quart et la demi-livre et établir d'autres comparaisons.

Quand toutes les pommes de terre ont été mises en sacs, il a fallu chercher le prix de vente. (La notion de profits et pertes s'applique très bien à cette situation.)

La démarche pour trouver le prix d'une livre ou d'un kilo n'est pas facile. D'abord il faut saisir que dans le sac de 50 livres, il y a 50 petits sacs de 1 livre, ce qui n'est pas évident pour tous. Pourtant, ceci constitue le fondement de la compréhension et de la résolution du problème. (On retrouvait cette même difficulté dans le calcul des heures travaillées.)

Ensuite, il faut comprendre que le prix doit aussi être séparé en 50. Ceci constitue la deuxième difficulté qui en est une de perception et de réalisation.

Cependant les gens savent très bien que le prix d'une livre est moins élevé que le prix de 50 lbs. À partir de cette connaissance, nous avons fait des suppositions.

Après avoir démontré qu'avec un sac de 50 lbs, je peux faire 50 sacs de 1 lb, le groupe est amené à faire des suppositions pour le prix de la livre. Ce travail peut se faire avec de la monnaie, des cartons ou des dessins au tableau pour représenter les 50 sacs.

La première supposition étant $1 la livre, on s'assure que la correspondance biunivoque est bien comprise, soit 1 lb: $1, 2 lb: $2, 31b: $3, etc.

En laissant les gens faire leur propre supposition et vérifications, on arrive à un peu moins de 10C la livre.

Si un sac d'une livre revient à 80, combien faudra-t-il vendre un sac de 5 livres?

Le travail s'est fait au tableau

1 lb	8¢	= 8¢	1 x 8¢ = 8¢
1 lb	8¢	= 16¢	2 x 8¢ = 16¢
1 lb	8¢	= 24¢	3 x 8¢ = 24¢
1 lb	8¢	= 32¢	4 x 8¢ = 32¢
1 lb	8¢	= 40¢	5 x 8¢ = 40¢

Il ne faut pas hésiter à mettre en parallèle les deux opérations pour bien saisir le lien entre l'addition et la multiplication.

Le calcul se fait ensuite sur la calculatrice. De la même façon, on peut faire
8 + 8 + 8 + 8 + 8 = 40 ou 5x8 = 40

En faisant la multiplication 5 x 8 = 40 à l'aide de la calculatrice, un participant a découvert qu'il arrivait au même résultat avec 8 x 5. Il venait de découvrir la commutativité. On en a profité pour voir que dans l'addition et la multiplication, on peut inverser les chiffres et arriver au même résultat.

Pour l'expérimentation du groupe d'achat, nous avons aussi acheté deux caisses de 24 boîtes de conserves. Ce matériel a été utilisé pour pour apprendre: le calcul du prix à l'unité, c'est-à-dire la division, mais aussi pour illustrer des expressions mathématiques telles 2x8 et 8 x 2 ou 4 x 6 et 6 x 4, etc.

Pour chercher le prix à l'unité, nous avons commencé par des emballages de 2 articles et avons trouvé le prix "arrondi''.

Avec 2 boîtes pour $4, nous défaisons l'emballage, séparons en deux unités distinctes pour faire comprendre que le prix doit aussi être séparé en deux. Nous travaillons avec des pièces de $1 pour bien "voir" la division. Nous reprenons de la même façon avec des emballages de 3 pour $6, 4 pour $8.

Lorsque le groupe a compris que pour trouver le prix à l'unité, il faut diviser le prix total par le nombre d'articles, nous poursuivons avec les prix réels.

Nous nous attardons davantage à travailler avec la calculatrice et la lecture des résultats. Dans l'opération $1.89 divisé en deux, il faut expliquer la valeur de 0.945, apprendre à lire et interpréter ces données. Le travail sur la calculatrice prend beaucoup d'importance pour certains et certaines, alors que d'autres préfèrent le calcul écrit. Nous respectons et encourageons les deux façons de faire.

En plus de chercher le prix à l'unité pour les caisses de conserves, nous avons utilisé ce matériel pour illustrer les multiplications. C'est facile d'illustrer les expressions 2 x 8 et 8 x 2 avec les boîtes de conserves en les plaçant en rangées. Nous pouvons facilement voir les tables de 2, 3, 4, 5, 6, 7, 8 jusqu'à 48.

C'est à force de répétitions et d'exemples concrets et variés que les gens comprendront et retiendront les multiplications.

Pour continuer la démarche et préparer la vente, nous avons acheté des produits non-périssables pour une somme d'environ $150.

Chaque article a permis d'introduire un apprentissage différent, d'approfondir ceux déjà vus, de travailler sur les 4 opérations et surtout d'apprendre à utiliser la calculatrice dans une situation réelle et à laquelle sont confrontés à chaque jour les participants et participantes.

Les apprentissages

L'addition et la multiplication: faire des emballages de 2 ou de plusieurs articles.	Trouver le prix des articles à partir du prix à l'unité.
La soustraction: retirer un ou plusieurs articles parmi ceux déjà choisis.	Chercher le nouveau prix,
La division: des emballages de 2 ou de plusieurs articles.	Trouver le prix à l'unité.
Les grammes et le kilo: le kilo d'arachides, le kilo de mais à éclater.	Trouver le prix du 100 gr.
Les taxes: les cassettes audio.	Le prix à l'unité plus les taxes.
Le litre: le savon à vaisselle en 4 l.	Le prix au litre plus les taxes.
La règle de trois: les rouleaux de papier de toilette	24 rouleaux en paquets de 2.

Le calcul des taxes est assez difficile à expliquer et à comprendre pour des débutants. Nous avons donc travaillé avec un tableau qui a été complété en atelier.

En partant du taux des deux taxes, nous avons établi que pour $100, il faut payer $15.56 de taxe. Puis nous avons cherché combien il faudrait payer pour $50, puis $10, puis $5 et $1.

Nous avons aussi calculé les taxes sur 50¢, 25¢ et 10¢. Nous avons ensuite complété le tableau qui permettait de calculer de façon assez précise la taxe sur les produits.

Achat	Taxes	Total
100 $	$15.56	$115.56
50 $	$ 7.78	$57.78
25 $	$ 3.89	$28.89
10 $	$ 1.56	$11.56
5 $	$ 0.78	$ 5.78
1 $	$ 0.16	$ 1.16
50¢	$ 0.08	$ 0.58
25¢	$ 0.04	$ 0.29
10¢	$ 0.02	$ 0.12

Bilan de l'activité

Le groupe d'achat, c'est-à-dire la vente comme telle des produits, s'est tenu pendant un atelier en après-midi. Toutes les personnes qui fréquentent Atout-Lire ont été invitées à participer en venant acheter des articles. Ce sont les gens des ateliers de calcul qui organisaient l'activité.

Ce qui a été fait avant l'ouverture:

• répartir en petite quantité certains produits: peser (par exemple des sacs de 200 grammes d'arachides) et calculer le prix de vente à l'unité;
• étiqueter les produits et les placer sur les tables.

Avant de commencer la vente des produits, on a pris le temps de faire quelques exercices de calcul (addition de montants d'argent), de façon à ce que les personnes de l'atelier se familiarisent davantage avec l'écriture de nombres décimaux. Sur leur calculatrice, les gens se sont donc exercés à faire le total de plusieurs produits.

Au moment de vendre les produits, pour que chacun puisse pratiquer le calcul du change à la caisse, les personnes des ateliers de calcul agissaient à tour de rôle comme caissier ou caissière.

Également, à la fin, les personnes ont calculé le montant total des ventes effectuées: combien d'argent il y avait dans la caisse en excluant le montant du change déjà versé dans la caisse avant les ventes.

Dans son ensemble, l'activité "groupe d'achat" impliquait les apprentissages suivants:

• calcul des poids (livres, grammes, kilogrammes, litres);
• initiation aux volumes (contenant, contenu);
• comparaison des prix en fonction des quantités (soustraction,
• multiplication);
• calcul des prix unitaires (multiplication, division);
• calcul des taxes;
• connaissance des décimales;
• calcul du change (monnaie et dollars).

L'expérience du groupe d'achat apparaît très positive.

Les personnes ont apprécié cette activité parce qu'elle était très concrète et permettait d'apprendre à calculer son argent, à comprendre comment estimer le prix d'achat de produits d'utilité courante. Après la vente, les gens étaient satisfaits d'eux-mêmes et du déroulement de l'expérience. En travaillant sur leur calculatrice ou sur la caisse enregistreuse, ils ont, pour la plupart, appris la façon d'écrire les montants d'argent (avec les cents - les décimales) et comment compter le change.

Cette activité pourrait s'étaler sur une période beaucoup plus longue en raison des nombreux apprentissages à y intégrer.

En ce sens, nous avons manqué de temps pour mieux approfondir certaines notions, surtout avec les personnes qui débutent en calcul.

Les principales difficultés que l'on peut identifier à ce niveau peuvent être résumées comme suit.

1. Les nombres décimaux: la lecture et l'écriture des nombres, particulièrement des sommes d'argent, avec points et monnaie (ex.: $3.04, $3.40, etc.);
   la lecture et l'écriture de montants en monnaie: régulièrement, on oublie d'écrire le point (ex. sur la calculatrice, on écrit 40 plutôt que .40).
2. Le sens des opérations: à quel moment on doit utiliser la division et la multiplication (si une boîte de pois coûte 36¢, quel prix vont coûter 3 boîtes? Et à l'inverse, si une caisse de 24 boîtes coûte $8.64, combien doit-on vendre une boîte?).
3. Trouver la différence entre deux produits (la soustraction).
4. Le calcul des taxes.
5. Le calcul du change en partant du prix fixé pour un produit: j'achète un objet qui coûte $3.38 et je paie avec$4.00. Compter 3.38, 3.39, 3.40, 3.50, 3.75, 4.00).
6. Les ventes et les rabais.

En reprenant cette activité, il faudrait l'inscrire dans une période de temps beaucoup plus longue. D'une part, cela permettrait d'effectuer une recherche plus précise des meilleurs prix pour l'achat de produits en grande quantité, de manière à assurer des économies réelles. Les personnes pourraient travailler à cette recherche ce qui constituerait un très bon exercice de comparaison de prix (chercher la différence en considérant les quantités en cause).

D'autre part, plus de temps paraît nécessaire pour mieux travailler et intégrer les multiples notions incluses dans une telle activité. Nous pensons entre autres à certains points particuliers comme la lecture et l'écriture des nombres décimaux, l'emploi de la calculatrice, le sens et l'utilisation appropriée des quatre opérations, l'étude des poids et des mesures, le volume, etc.

Les apprentissages à faire par le travail sur un groupe d'achat sont nombreux et leur degré de difficulté diffère. Ceci permet d'adapter divers exercices aux divers niveaux de connaissances des personnes. Alors que certaines travaillent par exemple sur la lecture et l'écriture des nombres décimaux (en étiquetant les produits), d'autres peuvent calculer les taxes.

En somme, ce quatrième module se voulait l'aboutissement des apprentissages de l'année. Devant l'intérêt manifeste de ce thème, nous pensons qu'il pourrait être facilement utilisé comme centre d'intérêt auquel pourraient se greffer tous les autres apprentissages des modules précédents. À notre avis et selon les commentaires reçus des participants et participantes, il y aurait lieu de reprendre l'expérience du groupe d'achat en raison des connaissances que l'on peut découvrir et des économies éventuelles que l'on peut y faire.

Conclusion générale

Nous avons voulu, en élaborant et poursuivant la démarche d'apprentissage présentée dans ce document, expérimenter un cheminement pédagogique basé sur la reconnaissance de l'expérience des participants et participantes (ce qu'ils sont et ce qu'ils savent) comme point de départ à l'apprentissage de notions mathématiques.

D'autre part, nous avons aussi axé notre travail sur la maîtrise d'habiletés fonctionnelles, c'est-à-dire que l'acquisition d'un savoir, de nouvelles connaissances, ne pouvait être dissociée du savoir-faire, ce dernier relevant de la préoccupation essentielle du transfert des acquis.

La démarche suivie a-t-elle portée fruit? Les participants et participantes ont-ils atteint les objectifs d'apprentissage fixés? En tant qu'animatrice, avons-nous assuré adéquatement le rôle de support et de ressource qui nous était dévolu? Les outils utilisés sont-ils pertinents au regard des objectifs définis? Somme toute, avons-nous réussi à proposer et à rendre effectives les conditions d'un apprentissage signifiant?

Ces questions méritent d'être fragmentées car elles font référence, contiennent et mettent en cause de nombreux éléments. On le sait, la réalité de l'apprentissage dans le cadre de l'alphabétisation populaire en est une globale qui sollicite une réflexion critique, laquelle s'étend au-delà des aspects normatif et sommatif qui constituent les repères traditionnels en éducation.

C'est ainsi qu'il nous apparaît important de considérer certains facteurs déterminant l'apprentissage, facteurs divers susceptibles d'influencer la qualité, le rythme et le niveau des acquisitions. Les conditions de vie, l'âge, la motivation, la qualité pédagogique de l'animation et les méthodes et stratégies d'enseignement sont ici à prendre en compte (F. Midy, 1992: 106).

Les principales caractéristiques du groupe de personnes qui ont participé aux ateliers de calcul pour niveau débutant peuvent être résumées comme suit:

• diversité dans le degré d'avancement de chaque personne: l'expérience mathématique, bien que de niveau débutant, varie selon l'expérience personnelle et les aptitudes de chacun;
• problème de lecture et d'écriture des mots et des nombres;
• richesse du vécu permettant de repérer des situations familières pouvant constituer du matériel pédagogique;
• difficulté à transférer les acquis, souvent en relation avec la capacité d'abstraction;
• les obstacles à l'apprentissage sont fréquemment liées à des problèmes de concentration, d'attention, de mémorisation;
• les conditions de vie sont généralement difficiles (les personnes ayant, pour la plupart, des prestations d'aide sociale comme seul revenu familial), et peuvent avoir un impact sur le processus de formation.

Il faut aussi considérer que certaines personnes démontrent un problème de surdité, ce qui accentue les difficultés d'apprentissage. D'autres personnes sont de langue maternelle autre que le français. L'âge des participants et participantes intervient également: l'atelier regroupe toute catégorie d'âge, de la vingtaine à la soixantaine.

L'assiduité des personnes aux ateliers de calcul, tout au cours du cheminement effectué, peut être un indicateur de leur motivation. Fréquemment, elles ont exprimé leur intérêt quant à la démarche poursuivie, soit en soulevant en atelier un problème vécu dans la semaine, soit en expliquant comment elles ont résolu un problème.

Partons du principe selon lequel la plupart des personnes apprenantes d'un groupe sont aptes à réussir ou à atteindre un objectif donné, mais chacune à son rythme (postulat soutenant l'approche de la pédagogie de la maîtrise, mastering learning). Ce principe commande, en quelque sorte, de penser en termes de formation sur mesure.

Nous croyons que pour la plupart des membres du groupe, les objectifs d'apprentissage sont en progrès: les personnes ne réussissent pas complètement la tâche mais manifestent des progrès quant à la maîtrise des nouvelles notions. Selon le cheminement personnel de chacun et chacune, les acquis diffèrent.

De façon plus précise, en ce qui concerne l'acquisition de concepts de base (numération, sens des opérations, signes et langage mathématiques), les participants et participantes sont donc en voie et en état d'apprentissage; ils arrivent à accomplir une bonne partie de la tâche proposée sans pour autant avoir atteint le seuil de la réussite.

Il nous faut de plus travailler davantage en vue de développer la compréhension, le raisonnement et la logique. Ces éléments représentent pour certains des objectifs parfois plus difficilement atteints en raison des caractéristiques mentionnées précédemment: entre autres, difficultés d'abstraction et de concentration. Chaque personne ne part pas du même point en raison des limites personnelles rencontrées. Cependant, et c'est ce qui importe, il demeure qu'un cheminement est amorcé et se continue. Chacun et chacune possèdent son propre rythme d'apprentissage, intimement lié à sa situation singulière, que nous avons tenté de respecter le mieux possible.

Bien que nous ayions eu à l'esprit la préoccupation constante de travailler à partir du connu, en utilisant des exercices de manipulation visant à concrétiser les apprentissages, ceci n'assure pas le développement de la capacité à transférer spontanément les acquis. Encore ici, cette aptitude est nourrie par la pratique, la répétition et la compréhension. Chez certains participants, le transfert des acquis à des situations de la vie courante se fait plus aisément. Pour d'autres, le cheminement doit être poursuivi.

Il convient également de souligner que le travail en groupe favorise certains apprentissages. L'entraide mutuel, selon le degré d'avancement des personnes, en plus de stimuler la motivation et valoriser les personnes, confirme leur capacité à résoudre des problèmes en calcul. Peu à peu, on forge son expérience mathématique.

Il est sans doute plus délicat d'aborder la question de la qualité pédagogique de l'animation (peut-on être à la fois juge et partie?). À ce propos, rappelons tout simplement que nous avons choisi une approche de résolution de problème. Le rôle de l'animation a été conçu principalement comme aide et support à l'apprentissage. Cette conception a orienté nos interventions qui visaient surtout à soulever des questions, à alimenter la réflexion, à faire appel aux capacités de raisonnement chez les participants et participantes.

Nous avons aussi tenté d'utiliser les erreurs non pas comme des fautes mais comme des pistes de solutions possibles que nous prenions le temps d'explorer pour mieux comprendre, par exemple, les données pertinentes d'un problème et le cheminement à faire pour le résoudre (tout en considérant les diverses façons d'y arriver, car souvent il n'y en a pas qu'une seule). Nous avons donc encouragé un processus d'apprentissage par essais-erreurs.

Quant aux outils pédagogiques retenus tout au cours de cette expérimentation, nous croyons qu'il est possible de les développer encore ou de les affiner. Déjà, avec le recul, nous voyons des améliorations à y apporter.

Par exemple, on se rend compte qu'il y aurait avantage à diversifier le matériel employé lorsque l'on aborde la numération. Ainsi, dans la démarche que nous avons suivie, nous avons utilisé principalement des verres et des jetons alors qu'il serait pertinent d'élargir l'éventail du matériel à d'autres objets tout aussi facilement accessibles bâtonnets de café, rondelles de jeu, feuilles de papier, etc., ceci dans le but de favoriser le transfert des notions. Il serait tout aussi souhaitable de varier la représentation de l'unité, de la dizaine et de la centaine de manière à mieux approfondir ou développer ces concepts.

C'est dans la pratique, en expérimentant des méthodes et des outils pédagogiques que l'on prend conscience de leur qualité et de leur lacune. Dans toute la démarche que nous avons fait, il est possible d'ajuster le matériel, de mieux articuler le déroulement des ateliers. Nous partons d'ailleurs de cette expérience, de ses forces et de ses faiblesses, pour planifier l'atelier de niveau débutant cette année.

Somme toute, et malgré ses imperfections, cette expérience d'apprentissage en calcul de base pour niveau débutant nous semble répondre aux objectifs qui y étaient rattachés. À la fin de cette "étape", les participants et participantes sont au cœur d'un cheminement qui progresse. Le rythme de cette progression est différent d'une personne à l'autre, ce qui s'inscrit tout à fait dans la démarche que nous proposions, où il s'avérait essentiel de respecter la différence entre les participants, où il fallait ajuster les activités au degré d'avancement des personnes composant le groupe.

La formation en calcul, comme en lecture et en écriture, participe d'un processus à long terme, où les miracles n'occupent aucune place. Il s'agit bien plus d'une démarche à long terme, où les connaissances peu à peu sont appelées à devenir des acquis lesquels, s'ils sont signifiants, trouveront, peu à peu toujours, une place dans la vie quotidienne des personnes en apprentissage.

Bibliographie

Artigue, Michèle, "Mathématiques: les leçons d'une crise", dans Sciences et vie no 180, sept. 1992, p. 46-59.

Beaudry, Gérard, Méthodologie spéciale, Le centre de Psychologie et Pédagogie. 1943, 793 p.

Dalbéra, Claude, "Calcul, vie quotidienne et alphabétisation", Alphabétiser? Parlons-en!, Genève, Unesco, Bureau international d'éducation, 1990, 16 p.

Gasquet, Sylviane, Apprivoiser les maths. Paris, Syros Alternatives, 1989, 140 p.

Ministère de l'Éducation, Guide pédagogique. Mathématique. Fascicule C. Les nombres naturels, Québec, Gouvernement du Québec, Direction générale du développement pédagogique, 1982, 65 p.

Midy, Franklin, L'évaluation des apprentissage Québec, Un visa pour L'alpha Pop no 6 1992, 120 p.

Remerciements

Nous remercions les participants et participantes des ateliers de calcul de niveau débutant pour leur précieuse collaboration à toutes les étapes de la démarche d'expérimentation dont nous présentons les résultats dans ce document.

Nous soulignons également la participation des gens qui fréquentent Atout-Lire aux diverses activités proposées, entre autres le groupe d'achat. Nous leur en sommes reconnaissantes.

Ce document a été rendu possible grâce à l'aide financière obtenue du Secrétariat d'État

Tous les textes de ce document peuvent être reproduits à condition d'en mentionner la provenance Pour commander des exemplaires, s'adresser à:

Atout-lire
266, rue St-Vallier Ouest
(Québec) G1K 1K2
(418)524-9353

Crédits

Projet réalisé par
Atout-Lire Août 1993

Coordination
Atout-Lire

Recherche et rédaction
Francine Loignon
en collaboration avec Linda Maziade

Mise en page
Francine Loignon

Correction de texte
Linda Maziade