Introduction

Nous ne sommes pas spécialistes. Nous n'avons pas suivi de cours d'université sur le sujet. Nous sommes des formatrices d'alphabétisation et nous travaillons depuis 5 ans avec un groupe d'handicapés intellectuels en calcul.

Nous avons remarqué un manque de matériel évident, pour les intervenants comme pour les participants. C'est dans ce contexte que nous voulons apporter notre contribution.

Nous avons d'abord voulu partager notre expérience, nos succès, nos erreurs, nos questionnements. En cours de projet, se sont ajoutés les résultats de nos recherches, de nos échanges, de notre étude et de nos réflexions.

Dans le cadre de notre projet «La danse des chiffres», nous avons rencontré une vingtaine de personnes qui travaillent comme nous auprès des adultes handicapés intellectuels de différents niveaux. Ces rencontres d'échanges ont été très intéressantes et ont nourri notre réflexion. Elles nous ont permis aussi de recueillir des titres de matériel de toutes sortes, liste qui a été intégrée au document.

Ce document constitue surtout un recueil d'activités de manipulation et d'exercices qui en découlent. Chaque activité comprend:

• parfois une introduction
• l'objectif visé
• le matériel nécessaire
• les pré-requis
• la durée approximative de l'activité
• son déroulement, (manipulation)
• symbolisation ou
• préparation d'un exercice écrit
• des exercices écrits
• une ou des variantes possibles

Notre ambition est d'enrichir votre réflexion et de vous apporter des suggestions pour vos ateliers.

En commençant ce projet, nous pensions relater notre expérience des 5 ans d'ateliers de calcul. À mesure que le projet avançait, il est devenu évident que nous ne pourrions expliquer qu'une partie de ces 5 années d'ateliers.

Nous sentons que notre approche s'enrichit au fur et à mesure que le projet avance , et aussi d'un atelier à l'autre, en expérimentant nos découvertes avec nos participants. Ainsi, même après avoir terminé et publié ce document, nous sommes convaincues que les idées qu'il contient vont continuer de progresser, de s'enrichir.

Dans tout le document, l'utilisation du masculin (participant) n'est nullement discriminatoire. C'est uniquement dans le but d'alléger le texte.

[Voir l'image pleine grandeur]

La Danse des chiffres

[Voir l'image pleine grandeur]

Échanges

Les rencontres avec les professeurs de S.F.I.S.(Service de formation à l'intégration sociale) et les formatrices d'alphabétisation ont été très intéressantes. Nous avons voulu connaître un peu ce qui se fait ailleurs pour enrichir notre démarche. Il en ressort que nous sommes tous plutôt isolés les uns des autres, d'un centre à l'autre.

À la suite des échanges, nous avons constaté une fois de plus qu'il y a très peu de matériel écrit sur le sujet (excepté le matériel maison)et beaucoup de productions sont pour les enfants. Pour certains adultes, cela ne les dérange pas, ça dépend de leur maturité. D'autres se sentent infantilisés, ils veulent être respectés dans leur réalité d'adulte.

On nous a dit souvent que les groupes sont hétérogènes, trop nombreux, et comportant parfois des problématiques de santé mentale. Ces caractéristiques alourdissent la gestion de plusieurs groupes.

De plus, la notion d'handicapé intellectuel ne comporte pas les mêmes balises selon les organismes, les endroits. Un tel est-il considéré handicapé intellectuel ou non? Léger, moyen ou profond? Le niveau moyen des groupes varie aussi beaucoup d'un endroit à l'autre.

Nous avons rencontré des intervenants des 2 réseaux d'éducation: d'une part les enseignants des commissions scolaires, autant dans le secteur «jeunes» c'est-à-dire jusqu'à 21 ans, que dans le secteur «éducation des adultes», dans les programmes SFIS et SIS; d'autre part les formatrices dans les groupes populaires d'alphabétisation. Nous avons senti et observé des différences importantes entre ces 2 réseaux. Ainsi, nous les abordons séparément.

Du côté des commissions scolaires

Les enseignantes rencontrées travaillent toutes avec des groupes hétérogènes de 11 à 18 personnes(généralement 15 ou 16 élèves).

Le temps consacré au calcul varie entre une période de 50min./sem. et 5 périodes de 3h/sem.

Les objectifs énoncés par les enseignantes que nous avons rencontrées sont puisés dans le programme du Ministère de l'éducation. Ils concernent le développement personnel et social: 1 'autonomie(gérer son argent personnel) , l'estime de soi, l'intégration à un emploi.

D'autres objectifs sont reliés à des apprentissages fonctionnels, comme le fonctionnement de la calculatrice, l'heure, etc... D'autres encore, ont trait à la numération comme telle: plus petit, plus grand, avant après, etc...

Très souvent, les enseignantes doivent réajuster leurs objectifs en cours d'année, pour mieux répondre aux besoins des élèves, selon le niveau de chacun et du groupe.

Voici des exemples de succès qu'elles vivent dans leur groupe: des étudiants se servent adéquatement de leurs coordonnées personnelles, font plus facilement des apprentissages quand ça touche le côté affectif ou dans un cadre de jeu. Quelques-uns font des achats personnels selon leur degré d'autonomie ou encore réussissent une recette de cuisine.

Les principales difficultés rencontrées sont le nombre élevé d'élèves dans les classes, l'hétérogénéité des groupes, ainsi que le manque de matériel adapté ou trop enfantin pour la clientèle.

Les enseignantes nous ont parlé de la résistance du milieu face aux objectifs d'autonomie des adultes handicapés intellectuels. Les progrès des adultes en autonomie révei1lent des peurs et réticences chez les adultes eux-mêmes, chez les intervenants de leurs centres de résidence et encore plus chez les familles naturelles. Cette résistance rend leurs efforts moins efficaces, et parfois même les annule.

Elles nous ont aussi parlé de leur travail avec enthousiasme et dynamisme. Pourtant, elles nous avouent du même souffle à quel point ce travail est fatigant et fantastique à la fois.

Du côté des groupes populaires d'alphabétisation

Les formatrices que nous avons rencontrées tout comme nous consacrent de 2 à 4 heures par semaine aux ateliers de calcul. Les groupes comptent de 5 à 10 participants.

Certains objectifs poursuivis concernent le climat d'apprentissage ou l'autonomie face à l'argent. Plusieurs formatrices souhaitent que les participants aient une idée de la valeur des objets, des services. D'autres objectifs concernent la latéralité, les opérations d'addition et de soustraction, la lecture et l'écriture des chiffres, l'heure, l'utilisation de la calculatrice, etc.. En général, les objectifs sont micro-gradués et doivent être réajustés régulièrement selon le groupe.

Les formatrices ont relaté des succès: le jeu de bingo, du magasin, l'utilisation de chansons, plus de discrétion au sujet de leur livret de caisse, un ordre de grandeur des vêtements ou autres achats, additions et soustractions.

Les difficultés exprimées concernent la valeur de l'argent, la mémoire, le lien entre l'apprentissage et le quotidien, la compréhension de l'abstrait, la concentration et l'incidence de santé mentale dans un groupe. Le manque de matériel a aussi été évoqué.

Globalement, les formatrices évaluent leur expérience de calcul avec les adultes handicapés intellectuels selon les progrès de leurs participants.

Progrès lents, mais perceptibles après quelques années, en comparant des nouveaux participants avec des plus anciens. Progrès valorisants! La motivation des participants constitue un encouragement à continuer.

De toutes ces rencontres d'intervenants, les différences entre les 2 réseaux se sont précisées. Dans les commissions scolaires, les groupes sont plus nombreux, le cadre du programme est plus délimité, ainsi que le temps total d'apprentissage.

Dans les groupes populaires, les budgets sont plus restreints, mais par contre, le ratio restreint permet d'apporter plus d'attention à chaque participant. Les formatrices ont plus de liberté par rapport au contenu des ateliers. Ces différences entraînent aussi une différence dans les approches. Les enseignants des commissions scolaires utilisent plus les exercices écrits.

Dans les 2 réseaux, chacun travaille avec les contraintes propres à son milieu.

Par nos rencontres d'échanges ainsi qu'à travers ce document, nous souhaitons établir un pont, pour nous enrichir les uns les autres, enrichir notre approche auprès des adultes handicapés intellectuels.

Principes et réflexions

Pendant nos 5 ans d'ateliers, nous avons travaillé le calcul en développant la compréhension logique des nombres. Nous avons beaucoup manipulé, en micro graduant les apprentissages.

Dans certains écrits consultés sur l'apprentissage du calcul chez les enfants, nous avons retenu l'importance de ne pas sauter d'étapes dans les apprentissages et l'importance de manipuler. Ces textes nous ont confirmé dans notre approche. Ils donnent aussi les étapes de la formation du concept de nombre chez les enfants. Nous avons supposé que ces principes s'appliquaient en grande partie à notre clientèle. Avons-nous raison de le supposer? Le débat est lancé.

D'autre matériel rencontré met l'accent sur la répétition de gestes, la mémorisation et sur l'arrondissement au dollar près ou au 10$ près: Monergo

Notre première réaction face à ce matériel: nous aurions voulu avoir connu ça dès le début de nos ateliers de calcul. En y réfléchissant, nous ne sommes pas sûres que ça aurait été préférable. Son approche est basée sur la répétition de gestes, mais pas sur le développement de la logique. Ça dépend probablement du degré de handicap de la personne et du groupe. Ça dépend aussi de l'implication des parents, des familles d'accueil, des éducateurs, etc...

Pourront-ils être vraiment autonomes pour faire des achats tout seuls? C'est relatif.. Les produits sont de moins en moins étiquetés. L'étiquetage des prix sur les tablettes est assez difficile à comprendre, même pour nous: caractéristiques du produit, numéro de code, etc...

Et la taxe! Comment savoir si un produit alimentaire est taxable ou non? Nous-mêmes, on s'y perd. Comment prévoir le montant qui sera affiché à la caisse? Pour un participant, comment prévoir s'il a en main suffisamment d'argent pour ce qu'il veut acheter?

À l'A.B.C., nous avons choisi de travailler avec l'argent juste. Plus tard probablement, nous verrons à arrondir des montants. De toutes façons, nous croyons que toutes les approches sont valables et complémentaires.

Voici des exemples qui illustrent l'importance de manipuler.

Certaines pièces de monnaie sont plus faciles à compter que d'autres. Avec les pièces d'un sou et d'un dollar, c'est plus facile. Les pièces de 10¢, ça devient plus facile si on travaille les dizaines, parce que notre système numérique est en base de 10. On peut alors faire un beau travail avec les 10¢ et les 1$ et éventuellement les 10$.

Les premières fois qu'un participant échange 10 pièces d'un sou contre une pièce de 10 sous, il peut se sentir «volé». C'est difficile à comprendre pour lui d'échanger un paquet contre quelque chose d'unique. C'est à force de faire et de refaire l'expérience de l'équivalence qu'il en sera finalement convaincu. Le pouvoir de conviction de la formatrice ne suffit pas, les exercices écrits non plus.

L'enseignement du calcul n'est pas linéaire, ni rapide. La numération se construit peu à peu. Par la manipulation, le participant peut s'approprier la situation, vérifier une supposition (ou devinette). L'important pour lui, c'est l'idée qu'il se construit à partir de cette manipulation.

Quand finalement il anticipe le résultat de sa manipulation et qu'il est certain de son calcul, elle devient inutile. Une étape est franchie pour lui. Il peut transcrire ses gestes en symboles. Il va plus loin dans l'abstraction. Après chaque manipulation, on la symbolise et on la traduit sur papier.

Notre rôle consiste à organiser en atelier les situations permettant de réutiliser plusieurs fois les mêmes connaissances dans des contextes différents. La progression des difficultés doit être micro graduée.

De plus, il nous faut verbaliser beaucoup. Nous faisons entrer le langage dans ces situations. Ce n'est pas suffisant pour faire comprendre, mais c'est indispensable. Nous posons souvent les questions «comment», «pourquoi», pour que les participants expliquent leur raisonnement même si c'est difficile pour eux.

Dans nos ateliers, nous avons aussi besoin d'intuition et d'observation. Nous devons sentir si notre groupe est prêt ou non à un nouvel apprentissage. Il ne s'agit pas de proposer des exercices à tout prix. Il ne s'agit pas non plus d'expliquer les façons, il faut les laisser chercher.

Nous devons aussi encourager dans l'atelier plusieurs procédures pour une même situation. Chacun peut chercher son propre chemin, sans quoi le participant répond ce qu'il croit que la formatrice veut entendre, sans comprendre vraiment.

Si on veut que notre matériel réponde aux besoins de nos participants, on doit s'attendre à en créer, à en adapter beaucoup. Quand un exercice bloque, nous cherchons la cause. Est-ce la mise en page trop chargée? Il est souhaitable de nous en tenir généralement à une seule consigne par page. Est-ce une progression trop rapide? Attention à nos attentes, à ce que nous, on trouve facile et évident! Est-ce la complexité d'un dessin à exécuter? Est-ce le manque d'intérêt pour le matériel choisi? Essayons avec un jeu ou des objets qu'ils aiment. Si finalement, on arrive à la conclusion qu'ils sont bloqués du côté logique, on supporte leur mémoire par une chanson, par la répétition de gestes ou un autre truc.

Notre rôle demande beaucoup de patience, nous le savons. Nous revenons sur ce qu'on a fait le mois passé, l'année passée. La relation avec la formatrice joue aussi. On encourage leurs efforts et leurs progrès minimes. Ils apprennent à être fiers d'eux et c'est là qu'ils nous surprennent.

Formation du concept de nombre

Cette question nous semble importante. Dans la période des échanges avec des enseignantes et des formatrices, nous avons eu la chance de rencontrer Madame Bernadette Janvier, professeure en didactique des mathématique à l'UQAM. Sa rencontre a été déterminante pour le déroulement du projet. Elle nous a entretenues de la formation du concept de nombre. Elle nous a conseillé un vidéo qu'elle a préparé à ce sujet avec son équipe. Nous vous le recommandons à notre tour: "Le concept de nombre et son acquisition chez le jeune enfant" (voir à la fin: Références. Madame Janvier et son équipe nous expliquent un test en 5 tâches, pour vérifier si un enfant (ou un participant) a acquis ou non ce «concept de nombre».

• Première tâche: dénombrement
  On lui demande de dire combien il y a d'objets devant lui. Les difficultés peuvent être de récitation: erreurs dans la suite des nombres, de coordination: le doigt qui ne suit pas la même vitesse que la récitation des nombres, ou d'organisation: compter 2 fois le même objet ou en oublier.
• Deuxième tâche: production ou formation d'une collection.
  On lui demande de préparer x objets. En plus des 3 difficultés du dénombrement, il peut y avoir un problème de mémoire. Il doit se souvenir du chiffre demandé.
• Troisième tâche: «N de plus, N de moins»
  On lui demande de mettre 4 objets de plus que le paquet en place, par exemple, ou 2 de moins. La maîtrise de l'ordre peut être partielle ou complète.
• Quatrième tâche: conservation
  On lui demande de dire combien il y a d'objets, quand le paquet a déjà été compté, mais déplacé et replacé. À ce sujet, voir le jeu du Sac de jetons, à la fin, dans «Suggestions pour terminer...».
• Finalement, cinquième tâche: comparaison de 2 collections d'objets différents. De quel côté il y a plus d'objets, moins d'objets? Comment faire pour qu'il y en ait «pareil», ou autant? Voir Activité de manipulation 1.

Certains de nos participants ont réussi ce test, d'autres non. De là, nous avons déterminé sur quoi mettre l'accent avec chacun. Voir aussi à ce sujet l'introduction au chapitre «Activité de manipulation 2», concernant les dizaines.

Convention

Symboles utilisés à l'A.B.C. des Manoirs et dans cet ouvrage.

[Voir l'image pleine grandeur]

N.B. Les billets de 50$ et 100$ ne sont pas utilisés dans ce document parce que nos participants les manipulent rarement.

Activité de manipulation 1

[Voir l'image pleine grandeur]

Matériel requis:
Objets à compter, faciles à manipuler comme des sous, des dollars, des bâtons, des jetons, etc... Pensez aussi que ces objets doivent être faciles à dessiner à l'étape des symboles.

Facultatif: Cartons des nombres 0 à 9 ou 1 à 9.

[Voir l'image pleine grandeur]

Pré-requis:
Savoir réciter les chiffres jusqu'à 9, les lire et les écrire.

[Voir l'image pleine grandeur]

Temps:
Environ une heure.

[Voir l'image pleine grandeur]

Démarche:
On distribue à chacun un nombre différent d'objets(nous dirons des sous) en désordre, de 1 à 9 ou selon le nombre de participants. Il serait intéressant d'intégrer le 0, mais le participant qui ne recevrait rien risquerait de se sentir pénalisé. Alors, cela pourrait être la formatrice qui a «zéro sou». Si votre groupe compte plus que 9 ou 10 participants, veillez à donner les plus gros nombres à ceux et celles qui ont plus de chances d'en saisir la valeur.

Si vous sentez que le groupe est prêt, vous pouvez «sauter des nombres». Exemple: si on a 7 participants, on peut distribuer 4$, 8$, 5$, 1$, 7$, 9$ et 2$. Personne n'a 3$ ni 6$. C'est plus difficile parce que cela diffère un peu de la récitation des nombres. Il est important de veiller à ce que personne ne se sente moins «chanceux» d'avoir un plus petit nombre de sous, dans la mesure du possible.

De même, il est important d'une fois à l'autre, de changer celui ou celle qui a moins de sous.

Il faut que le doigt se déplace au même rythme que la récitation des nombres.

À tour de rôle, ils vous disent leur nombre. La formatrice les écrit au tableau ou on choisit le carton de ce chiffre. Au besoin, on peut faire un exercice de lecture de ces nombres.

La formatrice demande de bien regarder les paquets de sous de tous les participants. Elle demande à chacun sa réponse qu'on écrit au tableau.
Il est important de ne pas réagir à chaque réponse donnée, ni négativement, ni positivement. Ça risquerait d'influencer ceux qui n'ont pas encore répondu. Cela court-circuiterait la réflexion. S'ils sont trop influencés par les réponses des autres, on peut demander qu'ils nous disent leur réponse dans l'oreille. On leur demande pourquoi ils pensent ça, on en discute.

S'il y a plus d'une réponse donnée, on compare 2 paquets de sous en faisant correspondre chaque sou d'un paquet avec un sou de l'autre paquet.
C'est la correspondance terme à terme. Exemple: François a 2 sous et Johanne a 4 sous. On déplace un sou de Johanne vis-à-vis un sou de François. Ils vont ensemble. Les 2 sous «se donnent la main». On fait de même avec les autres sous. Finalement, tous les sous de François sont placés, alors que pour Johanne, il en reste encore 2.

Le paquet où il ne restera plus de sous pour correspondre à l'autre sera celui du plus petit nombre. Le participant qui a ce nombre se place debout au mur, avec éventuellement le carton de son nombre.

Chacun donne sa réponse etc... quand on l'aura trouvée, le participant correspondant à ce nombre se place debout, derrière le premier participant. Ainsi de suite jusqu'au dernier, qui a le plus de sous, le plus gros nombre, le plus riche.

Il est important de verbaliser ce qu'on fait, de répéter souvent les expressions le plus, le moins, le plus gros, le plus petit, pour que les participants en saisissent bien le sens. Alors, on a placé les nombres en ordre croissant.

Préparation d'un premier exercice écrit:
Les nombres inscrits au tableau sont mêlés.

La formatrice l'écrit en bas sur une nouvelle ligne et on barre ce nombre sur la ligne du haut etc... jusqu'au plus grand.

Revenir aux paquets de sous au besoin. Plus tard on pourra demander à un participant de venir faire l'exercice au tableau.

Exercice écrit:
On donne une dictée de chiffres de 1 à 9 ou de 0 à 9 , dans un autre ordre que celui du tableau, sur une seule ligne. La dictée de nombres à plusieurs participants dans un cahier peut poser le problème suivant: ils écrivent de différentes grosseurs et n'arrivent pas tous à la fin de la ligne au même nombre. Nous avons résolu ce problème en leur faisant écrire leurs nombres sur une feuille à carreaux, un nombre par carreau. On pourra se servir de cette feuille pour pratiquer la lecture des nombres.

Autre possibilité: On peut aussi leur demander de découper les carreaux de nombres qu'ils viennent d'écrire en dictée et de les replacer en ordre. C'est plus facile parce qu'ils peuvent les déplacer.

Préparation d'autres exercices écrits:
Avant de faire un exercice sur une feuille, on fait un exemple semblable au tableau.

[Voir l'image pleine grandeur]

Compter des objets dessinés ou fixes, c'est beaucoup plus difficile pour un participant, parce qu'il ne peut pas déplacer les objets à mesure qu'ils sont comptés.

Il lui faut organiser le comptage pour qu'il soit efficace. C'est d'autant plus important quand le nombre à compter est grand. On l'encourage alors à marquer chaque objet, à mesure qu'il est compté. Bien que généralement gagnante, il faut savoir que cette technique comporte un inconvénient: si le participant a besoin de recompter, la marque est déjà faite, ce qui peut occasionner des erreurs. Il devra alors faire une nouvelle marque ou effacer.

Certains participants préfèrent procéder par un balayage de la surface de l'ensemble. Si c'est fait méthodiquement, cette technique fonctionne aussi.

Après avoir dénombré et étiqueté les ensembles du tableau, on détermine le plus petit nombre, l'ensemble qui a le moins d'éléments, le moins de choses.

Quand c'est difficile, que certains participants hésitent entre 2 ensembles, on leur fait effectuer la correspondance terme à terme en leur demandant de relier par un trait chaque élément d'un ensemble à un élément de l'autre, au tableau, puis sur leur feuille. Ils verront par le ou les éléments restants quel ensemble a le plus d'objets et celui qui en a le moins.

[Voir l'image pleine grandeur]

Exercice sur une feuille: no.1
Garder le matériel sorti pour manipuler au besoin.
Vous pouvez trouver des exercices semblables dans plusieurs cahiers et documents, par exemple La Boîte à Crayons.

Variantes:
On peut refaire l'exercice en changeant le matériel à manipuler.

Une variante plus difficile consiste à refaire cet exercice en ordre décroissant. La difficulté vient du fait que les participants ne peuvent plus se fier à la récitation des nombres quand ils comptent. Commencer avec peu de nombres, parce que ça demande plus de temps.

On peut refaire l'exercice avec les nombres 10 à 19 ou 0 à 19, etc...

Exercice 1

Nom: ___________

[Voir l'image pleine grandeur]

Introduction à la manipulation 2

À L'A.B.C. des Manoirs, dans l'histoire de nos ateliers de calcul, nous avons travaillé des dizaines très tôt. Par contre, en étudiant pour préparer ce document, nous avons compris qu'il y a plusieurs étapes avant d'aborder les dizaines et la valeur de position(valeur du 2 dans 26). Nous vous les partageons telles que nous les comprenons.

Nous devons d'abord travailler la numération . Nous amenons les participants à construire solidement la série des nombres, en répétant l'addition de 1, c'est-à-dire à bien connaître l'ordre des nombres et à avoir une idée claire de la distance entre eux.

La première étape sera une approche globale et d'abord orale.

Nous attirons l'attention des participants sur l'ordre des nombres. Voici quelques exemples d'exercices de récitation:

1^e Réciter les nombres à partir de 1, le plus loin possible.

2^e Réciter les nombres à partir de 1 jusqu'à un nombre déterminé, à l'intérieur de ce que le participant sait compter, bien sûr

3^e Réciter les nombres en intercalant des mots. Exemple:1 pomme, 2 pommes, 3 pommes... 1 belle semaine, 2 belles semaines, etc...

4^e Réciter à partir d'un nombre différent de 1.

5^e Compter à reculons ou à l'envers.

6^e Compter 2 par 2 la suite croissante ou décroissante.

7^e Réciter en avant par exemple, 5 nombres à partir de 8, ou en arrière 2 nombres à partir de 9, etc...

Pour l'apprentissage de la lecture et de l'écriture des nombres, on peut avoir recours à une bande numérique avec les chiffres de 1 à 19, qui peut-être allongée au besoin. Ça peut être une bande pour le groupe ou une par participant, comme outil personnel. L'outil que nous utilisons à l'A.B.C. est notre page de bingo que vous trouverez à l'annexe 2.

Le participant cherche comment écrire quatorze, ou comment lire 14, en comptant sur la bande numérique ou la page de bingo jusqu'à ce nombre. Ce sont des outils de mémorisation qui se veulent temporaires.

L'étape suivante consiste à découvrir des régularités dans la suite écrite. Plusieurs outils peuvent aider à ces prises de conscience, à condition que la dizaine représente une période, un intervalle régulier et non un regroupement.

Une habitude qui peut aider à comprendre la structure du système numérique est d'utiliser des expressions comme "Vingt c'est 2 dix" "Trente, c'est 3 dix" "Trente et un, c'est 3 dix et un".

On peut aussi utiliser la page de bingo pour leur faire découvrir des régularités. On leur demande de colorier toutes les cases où le 9 apparaît et discuter de la position de ces cases.

Ils peuvent aussi découvrir la ressemblance de la suite de 10 à 19 avec celle de 1 à 9. C'est la même chose avec les autres dizaines.

Au terme de cette étape, les participants peuvent écrire des suites de nombres, même assez grands. Ils comprennent qu'entre 30 et 40, tous les nombres commencent par un 3, c'est la famille des trente. Ça n'implique pas nécessairement la compréhension des quantités impliquées, ni même de pouvoir lire ces nombres.

Il faut leur faire compter souvent un à un des jetons, des objets, des nombres de plus en plus grands jusqu'à 69 s'ils le peuvent, ou même plus).

On leur fait remarquer les inconvénients de cette façon plus lente de compter: la fréquence des erreurs, l'obligation de reprendre à 1 à chaque erreur, le temps que ça implique.

Quand on pense que le groupe est prêt, ou plutôt quand quelques-uns dans le groupe sont prêts, on propose une façon plus rapide de compter des objets que le comptage un par un: compter par dizaine. On continue de laisser le libre choix de la façon de compter le plus souvent possible. Certains vont toujours compter un par un, malgré toutes nos explications. Ils en ont besoin. D'autres choisissent la façon la plus rapide. Ils ont compris que ce raccourci(comptage par dizaines) équivaut avantageusement au comptage un par un. Notre rôle est de créer les conditions pour cette prise de conscience.

En français, les nombres entre 60 et 100, et spécialement entre 69 et 100 sont très difficiles à lire et à écrire. La plupart des participants confondent 70 et 90, 73, 63 et 93, etc..

Quatre-vingts aussi est difficile, parce qu'il suggère 4. À l'A.B.C., nous revenons très souvent à cet apprentissage, presqu'à chaque semaine, souvent avec notre bingo ou une dictée de nombres.

Probablement qu'il serait profitable de traduire souvent ces nombres par les expressions: "Soixante-treize, c'est sept- dix et trois ", comme expliqué précédemment.

Exercice de manipulation 2

Objectif:
Amorce des dizaines et valeur de position.

[Voir l'image pleine grandeur]

Matériel requis:
Pots de yogourt (ou autres contenants) et objets à compter: sous noirs, bâtons de popsicle, jetons, dollars, etc...

[Voir l'image pleine grandeur]

Pré-requis:
Savoir réciter les nombres jusqu'à 19 au moins, les lire et les écrire, avoir compté souvent un par un des grands nombres, bien connaître l'ordre des nombres et avoir une idée claire de la distance entre eux(voir l'introduction de ce chapitre).

[Voir l'image pleine grandeur]

Temps:
Environ 2 ou 3 heures.

[Voir l'image pleine grandeur]

Démarche:
On distribue à chacun 2 pots de yogourt et un nombre de sous variable à chacun, entre 10 et 19, en désordre. Quelqu'un pourrait aussi avoir un nombre inférieur à 10, par exemple 8 sous. On a choisi cette façon plutôt que d'avoir tous un même nombre à manipuler, pour éviter qu'ils ne se fient à leurs voisins.

Consigne:
Compter les sous.

Il faut que le doigt se déplace au même rythme que la récitation des nombres. À tour de rôle, ils nous disent leur nombre et comment ça s'écrit. La formatrice écrit ces nombres au tableau. On pourrait en profiter pour réviser l'ordre croissant. Voir l'exercice de manipulation 1.

L'exercice peut se faire en groupe oralement ou par écrit. Prévoir le temps nécessaire.

Consigne:
À chaque fois qu'on a 10 sous, on les met dans un pot de yogourt, pas 9 , pas 11. On appelle ça une dizaine . Dizaine, ça ressemble à dix. C'est un paquet de 10.

Chacun le fait.

Verbalisation et valeur de position:
Treize, ça s'écrit 13. La formatrice demande ce que représente le 3 dans 13. Chacun dit ce qu'il en pense. Elle attire leur attention sur les 13 sous préparés par un participant: 10 sous dans un pot et trois sous à côté du pot de yogourt. On appelle ça des unités: 3 unités, ou bien 3 sous tout seuls.

Elle demande ensuite ce que représente le 1 de 13.

La formatrice tente de leur faire deviner, en les faisant observer les 13 sous, répartis en 1 pot de 10 sous et 3 sous à côté. Chacun dit sa réponse. Elle laisse les participants s'exprimer sans réagir, négativement ou positivement.

Finalement, elle explique que ce chiffre 1 nous dit combien il y a de dizaines, combien de pots de yogourt. Si vous n'avez jamais travaillé les dizaines, il est fort probable que personne ne devinera le sens du chiffre 1 (selon le niveau de handicap de votre groupe).

La formatrice pose les mêmes questions pour les autres nombres, selon le temps disponible et leur concentration bien sûr.

Exemple: Dix-sept ça s'écrit 17. Que veut dire le 7 dans 17? Que veut dire le 1?

Préparation des exercices écrits:
La formatrice choisit un nombre entre 12 et 19(10 et 11 ne permettraient pas de distinguer aussi bien les dizaines des unités mais ils peuvent être employés à l'occasion).

Elle dessine le chiffre de façon très stylisée pour que ce soit facile à reproduire, selon le matériel utilisé. Exemples: Ce dessin représente 10 sous dans un pot de yogourt (une dizaine) et 3 sous seuls(3 unités). Donc:13¢

[Voir l'image pleine grandeur]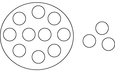

Ce dessin représente un pot de yogourt(une dizaine) et 3 bâtons seuls(3 unités). Donc 13 bâtons.

[Voir l'image pleine grandeur]

On compte par dizaines les sous ou les bâtons. «Combien y en a-t-il dans le pot? Dix. Alors on dit dix(en faisant le geste de pointer ou d'entourer le pot). On change de façon de compter et on dit onze, douze, treize(en pointant les unités). Compter par dizaines, c'est une façon plus rapide de compter. Compter un par un, c'est une façon plus lente de compter.

Exercices écrits: no.1 et no.2
Laisser le matériel sorti pour manipuler à nouveau au besoin. Pour leur faire tracer les cercles, nous avons utilisé le fond de verres de plastique.

L'exercice que vous faites effectuer est toujours précédé d'une période de manipulation. Il est directement relié à cette manipulation en la symbolisant. Il en constitue le prolongement.

Donc, il est évident que si vous avez manipulé des sous et des pots de yogourt, l'exercice écrit se rapportera aux sous et aux pots de yogourt.

Gardez les exercices écrits sur les bâtons pour le jour où vous avez manipulé les bâtons.

Quand vous vérifiez avec eux leur travail, vous en profitez pour leur faire compter par dizaines chaque numéro.

Variante 1: Les autres dizaines

Même exercice de manipulation avec des nombres plus grands. On demande de compter 32 sous par exemple, ou un nombre différent à chacun, sans préciser la façon de compter. On observe leurs façons de procéder, c'est révélateur. Puis, on attire leur attention sur les façons de compter des autres participants. On invite ceux qui ont compté 1 par 1 à compter par dizaines; ceux qui ont compté par dizaines font la preuve en comptant 1 par 1. Est-ce que ça donne le même nombre?

On compte 10 par 10 avec le premier couplet de la chanson «La danse des chiffres»(voir à la fin de ce chapitre). Il est bon de ralentir un peu quand on arrive aux nombres, pour bien comprendre ce qu'on chante. On pointe les dizaines une à une, à mesure qu'on chante un nombre. Attention, le rythme change un peu quand on arrive à «Et soixante, soixante-dix». Ces nombres ont plusieurs syllabes. Le rythme de comptage doit s'ajuster à celui de la chanson.

Quand on compte par dizaines, 32 par exemple, à l'aide de la chanson ou pas, on dit dix, vingt, trente bien sûr. «Là, on change de façon de compter pour les unités.» On compte un par un à partir de 30: 31,32..

Exercices écrits: No. 3 et 4

Variante 2: Bâtons avec élastiques.

On peut refaire l'exercice en changeant le matériel à manipuler. Exemple: 10 bâtons qu'on regroupe en dizaine avec un élastique.

Dessin suggéré pour symboliser ce matériel:

[Voir l'image pleine grandeur]

Ce dessin représente un paquet de bâtons attachés(une dizaine) et 3 bâtons seuls(3 unités).
Attention à la cohérence. Si vous convenez qu'il y a toujours 10 bâtons entourés d'un élastique, ne rangez pas l'ensemble de tous vos bâtons avec un élastique. De même pour les bâtons dans les pots, ne rangez pas les bâtons inutilisés dans les pots même empilés. Cela risquerait d'apporter de la confusion chez certains, parce qu'il n'y en aurait pas 10 comme convenu.

Variante 3: Comptage de doigts.

On demande à un participant de montrer 6 doigts, par exemple. Les autres vérifient s'il y a bien 6 doigts.

Puis, on demande à un autre de montrer 12 doigts, à Martin par exemple, c'est impossible , il a besoin d'une autre participante pour l'aider, disons Annie. Elle montrera 10 doigts et représentera une dizaine, alors que Martin montrera 2 doigts, c'est à dire les unités. Les autres participants comptent les doigts de la façon qu'ils veulent, lente ou rapide.

On peut procéder de la même façon pour les nombres plus grands, en déterminant un participant par dizaine et un pour les unités.

Variante 4: Enveloppes.

Si vous disposez d'un lot d'enveloppes identiques, vous pouvez vous en servir pour représenter des dizaines. Les unités seront des papiers identiques aussi, à insérer dans les enveloppes, par exemple 10 triangles rouges.

Vous devez prévoir des dessins simples pour symboliser vos manipulations. Par exemple:

[Voir l'image pleine grandeur]

Quand les triangles sont dans les enveloppes, c'est presque impossible de les compter un à un sans les sortir, C'est pourquoi nous conseillons ce matériel après avoir beaucoup manipulé des bâtons, des sous, des jetons, etc... Ça incite à compter par dizaines, la façon rapide.

Un avantage à utiliser ce matériel: après un certain temps, on peut passer à la manipulation des centaines en utilisant des enveloppes plus grandes, qui contiennent 10 petites enveloppes chacune et peut-être même, qui sait, aux milliers!

Variante 5: Les âges

On peut travailler les âges de chacun des participants de l'atelier et de la formatrice. C'est abstrait. On a besoin de manipuler ces nombres avec un matériel où l'unité représente 1 an. Chacun prépare tous les âges. À chaque fois, on écrit le nombre, on lit .Cet atelier est assez long, selon le nombre de participants du groupe.

Exercice écrit: no. 5

Variante 6: Âge - 1, âge + 1.

On refait un atelier semblable à la variante 5, mais chaque participant prépare les bâtons(ou autre) de son âge à lui et écrit le nombre de son âge.

Puis, on leur demande quel âge ils avaient l'an passé. Certains s'en souviennent. Pour ça, on enlève un bâton, pour 1 an de moins. Ils recomptent. Ils écrivent ce nombre. Certains changeront peut-être de dizaine. Si vous voulez aborder cette notion et que l'âge de personne dans le groupe ne s'y prête, vous pouvez inventer un personnage pour la circonstance. Puis, on leur demande quel âge ils auront l'an prochain. Pour ça, ils reviennent d'abord à leur âge actuel et ils ajoutent un bâton de plus. Ils écrivent ce nombre.

Exercice écrit: no. 6

Exercice 1

Nom: ___________

Écris à droite, combien il y a de bâtons. Compte de la façon la plus rapide.

[Voir l'image pleine grandeur]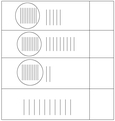

Imprimer l'exercice complet

Exercice 2

Nom: ___________

Dessine le nombre de bâtons demandé, regroupés par dizaines.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 3

Nom: ___________

Écris à droite, combien il y a de bâtons. Compte de la façon la plus rapide.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 4

Nom: ___________

Dessine le nombre de bâtons demandé, regroupés par dizaines.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 5

Nom: ___________

Exemple suggéré

Dessine autant de pots et de bâtons que l'âge de chacun

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 6

Nom: ___________

Écris ton âge dans le carré et dessine autant de bâtons que ce nombre.

[Voir l'image pleine grandeur]

Quel âge avais-tu l'an passé? Dessine autant de bâtons que ce nombre.

[Voir l'image pleine grandeur]

Quel âge tu vas avoir l'an prochain? Dessine autant de bâtons que ce nombre.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Danse des chiffres

(Sur l'air de «Ah vous dirais-je maman»)

Connais-tu la danse des chiffres?
Je sais compter dix par dix:
Dix, vingt, trente, quarante, cinquante,
Et soixante, soixante-dix,
Quatre-vingts, quatre-vingt-dix,
Et je suis rendu(e) à cent!

Connais-tu la danse des chiffres?
Je sais compter cinq par cinq:
Cinq, dix, quinze, vingt, vingt-cinq, trente,
Trente-cinq, quarante, quarante-cinq,
Connais-tu la danse des chiffres?
Je sais compter cinq par cinq.

Activité de manipulation 3

Objectif:
Identification des pièces 1¢, 5¢, 10¢, 25¢ et leur symbole.
*Peut-être l'identification du 25¢ est-il prématuré pour votre groupe.

[Voir l'image pleine grandeur]

Matériel requis:
Monnaie véritable si possible répartie ainsi: 1, 2 ou 3 pièces par participant de 1¢,5¢, 10¢ et 25¢.

[Voir l'image pleine grandeur]

Pré-requis:
Savoir lire et écrire les nombres 1, 5, 10 et 25.

[Voir l'image pleine grandeur]

Temps:
Selon les exercices écrits choisis, une à deux heures.

[Voir l'image pleine grandeur]

Démarche:
Identification des pièces et symboles. On distribue tous les sous mentionnés au «matériel requis».

Consigne:
On demande aux participants de placer devant eux une pièce de chaque sorte.

Ça fait combien de pièces? 4 pièces. Ensemble on observe chaque pièce, on la décrit, on la nomme. On regarde des 2 côtés. On trouve le nombre qui indique sa valeur. On compare avec les autres pièces semblables.

Exemple: la pièce de 5¢ avec les autres 5¢ sur la table. Puis on compare les différentes sortes de pièces. Quelques-uns connaissent peut-être déjà ces pièces.

On écrit au tableau chaque symbole et on explique que ces symboles ne sont pas universels. On s'entend entre nous pour représenter les pièces de cette façon. Dans d'autres centres ou écoles, on les écrit peut-être autrement.
On verbalise beaucoup, on utilise souvent le mot pièce. Par exemple, on demande aux participants de trouver telle pièce qu'on montre sans la nommer. On demande de la nommer, de nous montrer au tableau son symbole, ou même de le dessiner au tableau. Inversement, on nomme une pièce qu'ils doivent trouver, ou on pointe le symbole qu'ils doivent lire, etc.

Exercices écrits:
Dictée de symboles de pièces sur une feuille à carreaux. Quand on fait dessiner les symboles, il faut éviter que trop d'énergie soit requise pour le dessin. On peut leur faire tracer les cercles à l'aide d'un objet rond. Après la dictée, on peut leur faire lire les symboles qu'ils ont écrits.

Exercice écrit: no.1

Variantes:

Identification d'autres pièces ou billets, en révisant les pièces et billets déjà connus. Selon la capacité de votre groupe, vous pouvez les introduire un à la fois ou plusieurs en même temps. Par exemple: tous les billets ensemble.

Attention au dessin des billets. Si les rectangles sont trop arrondis, on peut les confondre avec le dessin des pièces.

Les pièces de 1 et 2 dollars doivent comporter absolument le signe de $ pour être distinguées des sous.

Exercices écrits: no.2 et no.3

Exercice 1

Nom: ___________

Relie chaque pièce avec son symbole.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 2

Nom: ___________

Relie chaque pièce ou billet avec son symbole.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 3

Nom: ___________

Dessine le symbole de chaque pièce ou billet.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Activité de manipulation 4

Objectif:
Valeur de la pièce de 5¢

[Voir l'image pleine grandeur]

Matériel requis:
1 ou 2 pièces de 5¢, 7 pièces de 1¢ ou plus, pour chaque participant, ainsi qu'une petite enveloppe ronde en forme de pièce de 5¢ pour chacun (voir à la fin du chapitre). Si on veut réviser l'identification des pièces, il faut aussi une pièce de 10¢ et une de 25¢.

[Voir l'image pleine grandeur]

Pré-requis
Savoir identifier la pièce de 5¢.

[Voir l'image pleine grandeur]

Temps
Selon les exercices écrits choisis, environ 45 minutes à 1 heure 30.

[Voir l'image pleine grandeur]

Démarche:
On peut commencer par faire une révision de l'activité d'identification des pièces et leur symbole.

Consigne:
Placer dans une main une pièce de 5¢. Dans l'autre main, mettre assez de pièces de 1¢ pour que cela soit égal des 2 côtés, de même valeur.

Quand nous avons fait cet exercice la première fois, nous avons été surprises de constater qu'ils ne savaient pas! Alors on attire leur attention sur le nom de la pièce. «Cinq sous ça vous fait penser à quoi? Cela veut dire 5 sous, cinq pièces de 1 sou». La plupart n'avaient pas fait le lien entre le nom de la pièce et sa valeur.

On explique bien le mot, valeur qu'on utilise souvent, à l'avenir: «On peut acheter la même chose avec ça (geste montrant une main) qu'avec ça (geste montrant l'autre main). Même si nos yeux ne voient pas la même chose des 2 côtés, c'est la même valeur, ça vaut la même chose. Cela revient au même».

Il est très important de réserver ce geste des 2 mains pour sa signification d'équivalence, de "même valeur". Par exemple, ne mettez pas des valeurs différentes dans les 2 mains en leur demandant de les additionner, ou autre.

Consigne:
Placer les 5 pièces de 1 sou les unes par-dessus les autres en une pile.

Certains participants malhabiles ont besoin d'aide. On discute encore de la valeur. La formatrice distribue les petites enveloppes rondes en forme de 5 sous: les 5 sous magiques.

Consigne:
Pour bien comprendre la valeur du 5 sous, on va faire rentrer les 5 pièces de 1 sou dans cette petite enveloppe magique.

Chacun le fait. On répète pourquoi on vient de faire ça, ou on pose la question à un participant.

Symbolisation:
La formatrice explique qu'elle va maintenant dessiner ce qu'on vient d'apprendre en symboles. Elle demande au groupe quel symbole représente la pièce de 5 sous et le dessine. «Le symbole qui nous dit que 2 côtés ont la même valeur, c'est le signe égal, comme ça. Qu'est-ce qui va de l'autre côté? C'est comme l'autre main». Elle dessine les 5 pièces. Le groupe les compte.

Au tableau il y a donc ceci:

[Voir l'image pleine grandeur]

Avec le groupe, on peut lire l'équation comme suit: «Une pièce de 5 sous, c'est égal, elle a la même valeur que 1,2,3,4,5 pièces de 1 sou», en pointant à mesure chaque élément. On peut demander aux participants de lire l'équation à leur tour. On peut revenir au geste des 2 mains au besoin.

Préparation des exercices écrits:

Monnaie en trop
La formatrice écrit ces symboles au tableau(l'équation précédente est effacée):

[Voir l'image pleine grandeur]

Vous remarquerez l'absence de signe =.

Consigne:
Les participants préparent les pièces en reproduisant ce qu'ils voient au tableau.

L'espace entre les 2 côtés doit être vraiment significatif. Ces 2 côtés représentent le contenu des 2 mains, comme dans le geste vu précédemment. On peut aussi leur faire séparer les 2 côtés avec une règle posée verticalement ou un crayon ce qui implique de les séparer aussi au tableau avec une barre verticale.

[Voir l'image pleine grandeur]

La formatrice demande: «Est-ce que c'est la même valeur des 2 côtés? C'est comme quand on met une pièce de 5 sous dans une main. Qu'est-ce que vous en pensez? Pourquoi? Ensemble on va compter s'il y en a 5».

On insiste encore sur le rythme de la récitation qui suit le rythme du pointage.

«Alors, qu'est-ce qu'on va faire pour que cela soit la même valeur des 2 côtés? Au tableau ou sur papier, pour enlever des pièces, on va les barrer, comme ça. Et maintenant, est-ce que c'est la même valeur? On va vérifier. Oui. Alors, quand c'est bien la même valeur des 2 côtés, on peut écrire le signe égal entre les deux, comme ça».

Monnaie en moins.
La formatrice écrit ces symboles au tableau:

[Voir l'image pleine grandeur]

Ou bien tels que choisis précédemment:

[Voir l'image pleine grandeur]

Dans un cas comme dans l'autre, il n'y a pas de signe égal.

Consigne:
Les participants préparent les pièces en reproduisant ce qu'ils voient au tableau.

«Est-ce que c'est la même valeur des 2 côtés? C'est comme le geste des 2 mains. On va vérifier en comptant ensemble: un, deux, trois, quatre. Est-ce que c'est la même valeur? Alors qu'est-ce qu'on va faire pour que ça soit la même valeur? On va ajouter une pièce, comme ça. Là, on vérifie, oui. Qu'est-ce qu'on va écrire pour montrer que c'est la même valeur? Oui,, = comme ça»

Puis, si vous avez travaillé la monnaie en trop une autre journée, révisez-la aussi pour préparer l'exercice 2.

Exercices écrits: no.1 et no.2
À chaque difficulté, on revient au geste des 2 mains, qui représente la notion de même valeur. On pose la question: «Est-ce que tu peux acheter la même chose avec ça(montrer une main) qu'avec ça(montrer l'autre main)?

Est-ce que c'est la même valeur? À gauche c'est combien d'argent? et à droite?» etc...

Variante -1- Comment compter les 5¢.

Vous avez besoin de 2 pièces de 5¢ et d'une dizaine de sous noirs chacun. On demande aux participants à quelle partie de leur corps le chiffre 5 leur fait penser? Les doigts de la main et les orteils. On va se servir de nos doigts pour compter les sous de la pièce de 5¢.

La formatrice dessine au tableau une pièce de 5¢ et 2 de 1¢:

[Voir l'image pleine grandeur]

Consigne:
Préparer les pièces comme au tableau.

On compte ensemble combien ça fait d'argent:
Quand on compte un 5¢ , on prend notre main. On pointe chaque doigt avec l'index de l'autre main.

Attention: un participant qui pointerait son auriculaire, son annuaire, son majeur et son index avec le pouce de la même main arriverait à 4 et risquerait d'oublier son pouce.

On peut aussi toucher la pièce de 5¢ successivement avec chacun des doigts de la main. Puis, on continue avec les autres pièces.

On arrive à 7¢. Elle écrit au tableau: = 7¢. Pourquoi =? Parce que de chaque côté du signe égal, c'est la même valeur: 7¢. Elle explique aussi le signe ¢ s'ils ne le connaissent pas.

Ensuite, elle prépare un autre exemple où la pièce de 5¢ n'est pas au début.
Exemple:

[Voir l'image pleine grandeur]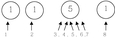

Jeu du magasin:

Vous pouvez étiqueter des bonbons avec des prix inférieurs à 10¢. Ils ont besoin d'une pièce de 5¢ et d'environ 9 sous noirs. Ceux qui préparent 9 pièces de 1¢ pour payer un bonbon à 9¢, ils ont réussi, mais vous les encouragez à faire un «échange», pour les inciter(sans leur dire) à utiliser la pièce de 5¢.

À chaque fois, vous leur demandez de compter leur argent pour vous payer.

Exercice écrit: no.3

À l'A.B.C., nous avons consacré presqu'une année à compter 5 par 5, entre autres avec le 2^e couplet de la chanson «La danse des chiffres». Malheureusement, nous avons constaté peu de progrès par rapport aux efforts consentis. Nous vous fournissons tout de même ce couplet (voir à la fin de ce chapitre), au cas où votre groupe serait plus avancé et en mesure d'attaquer cet apprentissage.

Variante -2- Valeur de la pièce de 10¢.

Vous avez besoin d'une ou deux pièces de 10¢ et d'environ 19 pièces de 1¢, ainsi que d'une petite enveloppe ronde en forme de pièce de 10¢ (voir à la fin du chapitre). Si vous voulez réviser d'autres activités, prévoir le matériel nécessaire.

On suit les mêmes étapes que pour la valeur du 5¢.

Quand on demande aux participants combien de pièces de 1¢ équivalent à la pièce de 10¢(geste des 2 mains), on attire leur attention sur le nom de la pièce en séparant bien les 2 mots: dix sous. Il faut verbaliser beaucoup. «On peut acheter la même chose avec ça(montrer une main) qu'avec ça(montrer l'autre main)».

Ensuite, on vérifie en posant la question: «Ça fait combien d'argent dans cette main-là(celle des sous noirs)?»etc...

Exercices écrits: no. 4 et no.5

Avant de faire l'exercice no 5, il est important d'avoir réalisé ces 3 manipulations, spécialement la dernière, celle qui concerne la pièce de 1¢. On peut préparer un exercice de monnaie en moins pour la pièce de 10¢, sur le modèle de l'exercice 2.

Variante -3- 10¢ et dizaines.

Avec cette variante, on va concilier le travail sur les dizaines avec celui de la valeur du 10¢. On a besoin de plusieurs sous noirs, des pots de yogourt et de quelques pièces de 10¢, selon le nombre choisi.

On leur demande de préparer 28 sous, par exemple, pour acheter un bonbon. Ils nous disent comment s'écrit ce nombre. Certains vont séparer les sous en dizaines dans les pots de yogourt. On encourage ceux qui ont compté un par un, à faire de même.

Consigne:
Mettre dans une main un des pots de yogourt(avec ses 10 sous) et dans l'autre, une pièce de même valeur.

Quand ils ont trouvé, ils sont prêts à faire un «échange». Il faut être bien sûr que c'est la même valeur dans les 2 mains. Alors, ils enlèvent ce pot de yogourt qu'ils remplacent par une pièce de 10¢. Ils comptent pour vérifier après chaque échange. Même échange avec l'autre pot.

Jeu du magasin: (voir variante 1)

Vous vendez des objets à des prix inférieurs à 1.00$. Il est préférable d'utiliser des objets réels.

Vous étiquetez chaque article. Vous aurez plus de succès avec des articles que vos participants aiment, parce que le côté affectif est sollicité. Vous pouvez même leur demander d'en apporter. Il faut veiller à ce que les prix demeurent réalistes. Vous leur fournissez des pièces de 10¢ et des sous noirs.

Consigne:
Lire le prix sur l'étiquette et préparer l'argent pour payer cet article.

À chaque fois, de nombreux exercices écrits peuvent être préparés sur ce principe. Vous pouvez refaire ce fameux jeu du magasin très souvent,, en changeant de thème: les fruits, les légumes, les articles de toilette, des petits jeux, etc..

Exercice écrit: no.6 (les fruits)

Note: Pour la valeur du 25¢, voir "Activité du manipulation 5".

Variante -4- Valeur de la pièce de 1$.

Cette manipulation est assez longue à faire.

Vous avez besoin pour chaque participant de 2 rouleaux de 1$, d'au moins 10 pièces de 10¢ et d'une pièce de 1$. Vous pouvez commencer l'atelier avec la «page de bingo», leur faire identifier quelques chiffres, dont 100. Puis oralement, en regardant ou non sur leur page de bingo, ils comptent à tour de rôle de 50 à 100 ou de 60 à 100.

Consigne:
Placer dans une main la pièce de 1$. Dans l'autre main (ou plutôt sur la table parce que la main peut difficilement contenir tout ça), mettre assez de pièces de 1$ pour que ça soit de la même valeur que la pièce de 1$?

Quand chacun a compté les 100 sous, la formatrice tente de leur installer ce paquet dans une main, pour faire le geste d'équivalence, avec la pièce de 1$ dans l'autre main. Ils expérimentent que 100, c'est beaucoup.

Dans ce gros paquet de sous, est-ce qu'on en a assez pour faire un échange?

On peut échanger directement 10 sous avec une pièce de 10¢, ou bien passer par les pots de yogourt.

À chaque échange, on recompte pour vérifier. On continue les échanges jusqu'à n'avoir que des pièces de 10¢.

Consigne:
Mettre dans une main la pièce de 1$. Mettre dans l'autre main assez de pièces de 10¢ pour que ça soit de même valeur des 2 côtés.

On peut symboliser la deuxième partie de cette manipulation en écrivant l'équation correspondante:

[Voir l'image pleine grandeur]

Variante -5- Valeur de la pièce de 2$

Prononcez bien le nom de la pièce: deux dollars.

Consigne:
Mettre dans une main une pièce de 2$. Dans l'autre main, mettre assez de pièces de 1$ pour que ça soit égal des 2 côtés, de même valeur.

Même démarche.
Nous suggérons de travailler les dollars seulement, pendant un temps suffisamment long, avant d'intégrer des sous. Les participants apprennent aussi comment lire et écrire les prix de dollars. Par exemple: trois dollars, ça s'écrit 3.00$.

Comment compter les pièces de 2$? Le participant touche 2 fois cette pièce, en disant un, deux. Il n'est pas nécessaire de placer la pièce de 2$ à gauche pour compter. Dans l'exemple suivant, le participant dit:

[Voir l'image pleine grandeur]

Il peut donc écrire l'équation:

[Voir l'image pleine grandeur]

Certains participants sont portés à écrire 6$ mais on leur fait remarquer qu'il n'existe pas de pièces de 6$ ni de billet. Les symboles (maison) avec les cercles et les rectangles désignent des pièces et des billets, alors que l'écriture avec le point et les 2 zéros (ou plus tard les chiffres de sous) , on appelle ça un prix.

Variante -6- Valeur du billet de 5$

[Voir l'image pleine grandeur]

Consigne:
Mettre dans une main un billet de 5$ . Dans l'autre, mettre assez de pièces de 1$ pour que ça soit égal des 2 côtés.

Comment compter les billets de 5$ avec les doigts? Comme les pièces de 5$ (voir variante 1) .

Variante -7- Valeur du billet de 10$

[Voir l'image pleine grandeur]

Consigne:
Mettre dans une main un billet de 10$ . Dans l'autre , mettre assez de pièces de 1$ pour que ça soit égal des 2 côtés .

Le jeu du magasin (voir variante 1) avec les billets de 10$ et les pièces de 1$, vous offre plusieurs occasions de renforcer l'apprentissage des dizaines.

De nombreux articles peuvent être vendus et achetés, selon plusieurs thèmes: des vêtements, des cassettes de musique, etc . .

Pour compter les billets de 10$ , il est préférable que le participant les place à gauche pour les compter d'abord, à l'aide de la chanson «La danse de chiffres» .

Exercice écrit: no .7

Variante -8- Valeur du billet de 20$

[Voir l'image pleine grandeur]

Consigne:
Mettre dans une main un billet de 20$. Dans l'autre, mettre assez de pièces de 1$ pour que ça soit égal des 2 côtés.

Puis, on leur demande si avec toutes ces pièces, ils en ont assez pour faire une dizaine. Contre quoi vont-ils échanger leurs 10 pièces de 1$?

Et ils continuent avec les pièces qui restent.

Consigne:
Mettre dans une main un billet de 20$. Dans l'autre, mettre assez de billets de 10$ pour que ça soit égal des 2 côtés.

Comment compter les billets de 20$? Le participant les place d'abord à gauche avec les billets de 10$. Il touche 2 fois ce billet de 20$ en comptant 10 par 10. Par exemple, il dit:

[Voir l'image pleine grandeur]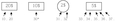

* Après 30, on change de façon de compter, on compte 1 par 1, en touchant 2 fois la pièce de 2$ et 5 fois le billet de 5$.

Exercice 1

Nom: ___________

Colorie les équivalences et barre la monnaie en trop.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 2

Nom: ___________

Ajoute la monnaie qui manque ou barre la monnaie en trop.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 3

Nom: ___________

Trouve la valeur de chaque ensemble et écris le montant.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 4

Nom: ___________

Colorie les équivalences et barre la monnaie en trop.

[Voir l'image pleine grandeur]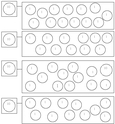

Imprimer l'exercice complet

Exercice 5

Nom: ___________

Dessine à droite assez de pièces de 1$ pour que ça soit égal des 2 côtés (autant d'argent)

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 6

Nom: ___________

Calcul

Dessine à droite les pièces de

[Voir l'image pleine grandeur]

pour payer les aliments.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 7

Nom: ___________

Dessine les pièces de

[Voir l'image pleine grandeur]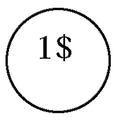

et/ou billets de

[Voir l'image pleine grandeur]

pour payer ces objets.

[Voir l'image pleine grandeur]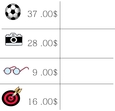

Imprimer l'exercice complet

Pochette de "Pièce magique"

1. Vous avez en bas le modèle d'enveloppe pour préparer la "pièce magique" (prévoir un papier résistant ou plastifié)
2. Au verso vous avez des copies de pièces disponibles.
3. Montage:

• prévoir 2 modèles comme ci-bas et 2 copies identiques de monnaies.
• coller l'illustration de la pièce choisie sur "ici":
• plier les pointillés dans le sens contraire de l'illustration (pas vers nous);
• courber la languette de dessous vers le haut en suivant le contour de la pièce;
• Placer les parties B sur B et brocher avec une très petite brocheuse ou coller;
• Laisser le haut ouvert pour introduire les pièces de monnaie.

[Voir l'image pleine grandeur]

Pièces de monnaie

[Voir l'image pleine grandeur]

Activité de manipulation 5

Objectif:
Valeur de la pièce de 25¢ et conservât:ion de la valeur avec différentes dispositions.
* C'est plus difficile à comprendre. Selon le niveau de votre groupe servez-vous de la chanson seulement (voir démarche basée sur la chanson après exercice écrit no: 2). Sinon, complétez la démarche avec elle. On peut aussi commencer par la chanson.

[Voir l'image pleine grandeur]

Matériel requis:
Vous avez besoin de 25 pièces de 1 sou au moins, 2 pièces de 10¢, 2 de 5¢,2 de 25¢.

[Voir l'image pleine grandeur]

Pré-requis:
Comprendre la valeur du 5¢, du 10¢, savoir décomposer un nombre à 2 chiffres en dizaines et en unités et savoir compter par dizaines(10 par 10) au moins jusqu'à 20.

[Voir l'image pleine grandeur]

Temps:
De 2 à 3 heures.

[Voir l'image pleine grandeur]

Démarche:
Basée sur la logique

On distribue les pièces. On peut leur demander de compter le nombre de sous noirs reçus.

Consigne:
Dans une main, placer une pièce de 25¢. Dans l'autre, placer assez de pièces de 1¢ pour que ça soit égal, de même valeur des deux côtés.

On insiste sur le nom de la pièce en prononçant distinctement 25.

On surveille le rythme de comptage et son organisât,ion. Un participant pourrait compter 2 fois le même sou ou en oublier.

Consigne:
Faire des échanges

La formatrice demande: «Avez-vous assez de sous pour faire une dizaine?... Si on met ces 10 sous dans une main, est-ce qu'il y a une pièce qu'on peut mettre dans l'autre main pour que ça soit égal des 2 côtés? Alors, quand on est bien sûr que c'est la même valeur des 2 côtés, on peut faire un échange. On enlève les 10 pièces de 1¢ et on les remplace par le 10¢.»

On leur fait vérifier si on a encore 25 sous en comptant l'argent. Il faut qu'ils commencent par la pièce de 10¢, en disant 10 et qu'ils continuent avec chaque pièce de 1¢ en disant 11, 12, etc... jusqu'à 25.

On continue les échanges en demandant si on a assez de sous pour faire une autre dizaine. Insistez sur le geste d'équivalence. À chaque échange qu'on fait, on doit d'abord s'assurer que ce qu'on enlève est vraiment de la même valeur que ce qu'on met en remplacement. Et ensuite, on recompte. C'est la preuve que notre échange a réussi.

Cette fois, on compte les 2 pièces de 10¢ en comptant 10 par 10. On fait appel à la chanson de la Danse des chiffres, mais on l'interrompt à 20. Ensuite, on change de façon de compter: les pièces de 1¢ en disant 21, 22, etc....

Puis, on leur demande de bien observer les sous qui restent, de les compter, de réfléchir s'il est possible de faire un autre échange. Quand ils y sont parvenus, on compte 10, 20.
Pour compter la pièce de 5¢, on utilise les 5 doigts de la main, comme on l'a déjà expliqué (voir activité de manipulation 4, variante 1).

Et voilà. On arrive à une équivalence importante. On reprend la pièce de 25¢ du début dans une main et on met dans l'autre main ces 2 p'tits 10¢ et le 5¢. Combien ça fait d'argent dans une main? Dans l'autre main? On les invite à fixer dans leur mémoire cette combinaison de pièces.

C'est, l'occasion de discuter de leur expérience du 25¢ et de la combinaison de pièces de l'autre main.

Exercice écrit: no.1

On peut aussi leur faire écrire au cahier l'équation

[Voir l'image pleine grandeur]

On peut aussi préparer des exercices du type «monnaie en trop» ou «monnaie en moins», comme dans l'activité de manipulation 4.

Conservation de la valeur avec différentes positions:

On dessine au tableau verticalement les symboles des 2 dix sous et du cinq sous. On demande combien ça représente d'argent dessiné au tableau. On peut leur demander de préparer devant eux l'argent comme au tableau. On encourage la discussion.

Consigne:
Changer la disposition des pièces comme ils veulent

On discute encore de la valeur de cet argent devant eux. Si personne n'y a pensé, empilez les 3 pièces avec le 5¢ dessus, dessous, puis au centre. Reposez la même question à chaque fois sur la valeur des 3 pièces.

Finalement, on leur demande de refaire le geste d'équivalence du 25¢ dans une main, et dans l'autre, combien de 10¢ et de 5¢?

Consigne:
Changer de main.
Placer le contenu de la main gauche à droite et celui de la main droite à gauche.

Qu'est-ce que ça change? Rien, c'est la même chose.

Au tableau, on inverse l'équation écrite au cahier:

[Voir l'image pleine grandeur]

et quelques autres:

[Voir l'image pleine grandeur]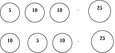

Exercice écrit: no.2

Démarche:
Basée sur la chanson

On distribue les feuilles de la chanson.

Consigne:
Bien écouter les paroles de la chanson qui nous parle de la valeur du 25¢ (premier couplet seulement)

On la chante en ralentissant pour accentuer les «2 p'tits dix sous» et le «cinq sous».

Consigne:
Placer dans une main une pièce de 25¢. Bien écouter la chanson pour savoir quoi placer dans l'autre main.

On rechante aussi souvent que nécessaire, en l'interrompant au besoin.

Variante 1:

Comment compter les 4 pièces de 25¢: démarche basée sur le 2^e couplet de la Chanson des sous (voir à la fin du chapitre Activité de manipulation 5).

Pré-requis:

Activité de manipulation 5 et valeur du 1$

[Voir l'image pleine grandeur]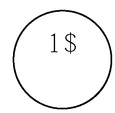

Après avoir bien écouté la chanson, on peut leur demander:

Consigne:
Mettre dans une main une pièce de 1$. Dans l'autre main, mettre assez de pièces de 25¢ pour que ça soit égal des 2 côtés, de même valeur.

Même démarche.

Exercice 1

Nom: ___________

Dessine à droite une seule pièce de monnaie pour que ça soit égal des 2 côtés, de la même valeur.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 2

Nom: ___________

Dessine à droite une seule pièce de monnaie pour que ça soit égal des 2 côtés, de même valeur.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Chanson des sous

(Sur l'air de «Gens du pays»)

Je peux compter mieux mon argent.
Un vingt-cinq sous, c'est quelle valeur?
Deux p'tits dix sous et un cinq sous,
C'est la même chose que vingt-cinq sous. You!

Et quand je compte les vingt-cinq sous,
Je dis vingt-cinq, cinquante, soixante-quinze,
Et un dollar; c'est la même chose,
Quatr'vingt-cinq sous, c'est un dollar. Yé!

Activité de manipulation 6

Objectif:
Comparaison de valeur des pièces (et billets), ordre croissant et décroissant.

[Voir l'image pleine grandeur]

Matériel requis:
Au moins 1 ou 2 pièces de chaque sorte, par exemple 1¢, 5¢, 10¢, 25¢.

[Voir l'image pleine grandeur]

Pré-requis:
Avoir travaillé la valeur de toutes les pièces impliquées.

[Voir l'image pleine grandeur]

Temps:
Environ une heure.

[Voir l'image pleine grandeur]

Démarche:
On peut, réviser la valeur d'une pièce ou l'autre.

Consigne:
Prendre une pièce de chaque sorte.

On discute ensuite de ce qu'on peut acheter avec chacune de ces pièces.

Consigne:
Placer ces pièces en ordre croissant de valeur.

Quelle est la pièce qui vaut le moins cher? Avec quelle pièce on peut acheter presque rien? Il y a une pièce qui vaut encore moins cher que les autres. C'est la pièce de 1¢. On la place à gauche, devant nous.

Dans les pièces qui restent, quelle est, celle qui vaut, le moins cher? Celle qui représente le moins d'argent? Le système monétaire canadien est trompeur: la pièce de 5¢ est un peu plus grosse que celle de 10¢. Les participants placent naturellement le 10¢ avant le 5¢ à cause de sa grosseur. Ça les induit en erreur pendant un certain temps. C'est pourquoi on doit revenir souvent à cette question.

Le retour aux 5¢ magiques et aux 10¢ magiques peut être utile. Ils peuvent empiler 5 pièces de 1¢ vis-à-vis la pièce de 5¢, 10 pièces de 1¢ vis-à-vis celle de 10¢ et comparer la hauteur des piles. La verbalisation est très importante pour prendre conscience de la valeur de ces pièces.

Certains participants comprennent mieux l'expression plus cher que celle de moins cher. On les amène à comprendre que «moins» est le contraire de plus . Exemple: «Le 10¢ est plus cher que le 5¢. Alors, on va attendre pour le placer. On cherche le moins cher, c'est le 5¢».

Les participants placent donc les pièces en ordre de valeur de gauche à droite, devant eux. Ils copient dans leur cahier les symboles de ces pièces dans l'ordre trouvé.

Exercice écrit: no 1

La formatrice prépare l'exercice au tableau, en faisant avec le groupe un exemple de comparaison de 2 pièces.

Variantes

À mesure que le groupe est initié à la valeur d'une nouvelle pièce ou d'un billet, on peut refaire des manipulations de comparaison et d'ordre de valeur.

Exercices écrits: no 2 à 5

L'exercice 5 suit une manipulation d'échanges, avec la répétition du geste des 2 mains (voir Manipulation 4, variante 3).

Exercice 1

Nom: ____________

Fais un X sur la pièce qui vaut: le plus cher.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 2

Nom: ___________

Mets les pièces en ordre de valeur sur la ligne.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 3

Nom: ___________

Fais un X sur la pièce qui vaut le plus cher.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 4

Nom: ___________

Fais un X sur la pièce ou le billet qui vaut le moins cher.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 5

Nom: ___________

Dessine la pièce ou le billet qui a la même valeur.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Introduction au chapitre des fractions - Activité de manipulation 7

Dès le printemps 1998, nous avons intégré des ateliers de cuisine, au rythme d'une fois toutes les 5 semaines environ. Nous avons commencé alors à travailler les mesures. Nous avons choisi les mesures impériales parce que les millilitres sont moins utilisés dans les recettes et que ce sont des plus grands nombres.

Nous avons d'abord travaillé toutes les fractions de la tasse à mesurer. Ils étaient bien mêlés! Nous avons alors mis de côté les fractions 1/3 et 2/3. À l'automne prochain, nous prévoyons y revenir, parce que les autres fractions ½, ¼, ¾ et l'entier sont acquises par l'ensemble du groupe.

Nous avons travaillé ces mesures systématiquement pendant 4 ateliers de calcul, souvent espacés de plusieurs mois ou même de plus d'un an.

Nous avons bien sûr mesuré ces quantités à chaque atelier de cuisine, c'est-à-dire une quinzaine de fois environ.

Important:
Les exercices de manipulation sont de beaucoup préférables à ceux d'observation de la formatrice qui manipule. Les participants sont plus concernés quand ils manipulent eux-mêmes.

Activité de manipulation 7

Objectif:
Lecture, écriture, compréhension, mesure des fractions ¼, ½, ¾ et de l'entier(1) et conservation des quantités.

[Voir l'image pleine grandeur]

Matériel requis:
Des tasses à mesurer de 1 tasse pour chacun des participants de votre groupe, de l'eau colorée, des grands récipients ou pichets, bols à soupe, des pommes et des couteaux pas trop coupants.

[Voir l'image pleine grandeur]

Pré-requis:
Savoir lire et écrire les chiffres 1,2,3 et 4.

[Voir l'image pleine grandeur]

Temps:
Environ 3 heures. Cette activité peut se faire en 2 étapes.

[Voir l'image pleine grandeur]

Démarche:
Chaque participant observe les écritures sur sa tasse à mesurer. Attirez leur attention sur les fractions de la tasse et non sur les millilitres. Au tableau, la formatrice dessine une tasse à mesurer avec les mêmes fractions que sur leur tasse. Identification de la ligne indiquant une tasse, au tableau et sur leur tasse. Elle entoure le 1 du tableau. Explication de l'importance de cette ligne dans les recettes.

Consigne:
Remplir sa tasse jusqu'à la ligne de 1 tasse.

On insiste sur la précision. On encourage les participants à se pencher pour que leurs yeux soient vis-à-vis la surface de l'eau colorée. On nomme la quantité. «Combien avez-vous d'eau dans votre tasse? C'est comme le lait, l'huile, le bouillon dans les recettes.»

On discute de ce qui arriverait si on vidait cette tasse d'eau colorée dans le bol. Jusqu'où l'eau irait? Il y aurait combien d'eau dans le bol? Il y en aurait moins ou plus? On les laisse discuter, deviner, sans donner la réponse. Puis chacun le fait et vérifie.

«Combien y a-t-il d'eau dans le bol? Il y en avait combien dans la tasse?»

Ensuite, on devine combien il y aura d'eau quand on la videra à nouveau dans la tasse à mesurer. On constate que c'est la même eau. Elle change de forme selon le contenant. Il y en a autant. De la même façon, on peut transvider cette eau dans un contenant très plat, comme une assiette, en leur faisant deviner avant, bien sûr. Puis, l'eau se retrouve dans les pichets.

Identification au tableau et sur leur tasse de la ligne d'une demi-tasse. La formatrice entoure la fraction ½ au tableau. «Ça s'appelle une demi-tasse. Une demi-tasse, c'est la moitié d'une tasse, c'est la même chose.» On utilise autant les mots moitié que demi,. On écrit aussi l'autre façon d'écrire la fraction, avec la ligne horizontale: 1.

On peut discuter de toutes les demies, de ce à quoi ces mots leur font penser. Ex. demi-heure, demi-lune, etc...

Consigne:
Remplir sa tasse jusqu'à la ligne de la fraction ½ tasse.

Les participants se penchent à nouveau pour que leurs yeux soient à la même hauteur que la ligne de l'eau. On nomme la quantité. On leur demande s'ils ont déjà mesuré des liquides ou des solides avec une tasse à mesurer.

Expérience des fractions avec la pomme: La formatrice distribue les pommes et les couteaux. «La pomme complète, ça s'écrit 1, une pomme comme la tasse à mesurer complète qui s'écrit 1.» Puis, on les invite à regarder la pomme de haut. «Qu'est-ce qu'on voit? Un rond, un cercle.» La formatrice dessine ce cercle au tableau. Ça représente toute la pomme. «Est-ce que ça se peut, une demi-pomme? Qu'est-ce qu'on fait pour avoir une demi-pomme?»

Consigne:
Couper sa pomme en 2 parties.

La formatrice aide à placer le couteau bien droit, pour que les deux moitiés soient le plus possible égales. «Ça fait combien de moitiés? Chaque moitié, c'est une demi-pomme. Comment ça s'écrit, une demi-pomme?» La formatrice écrit la fraction au tableau. C'est comme une demi-tasse.

Chaque participant prend dans sa main une demi-pomme et nomme la fraction ½. On fait le lien avec l'écriture de la fraction: 1 sur 2, c'est un morceau( le chiffre du haut), quand la pomme est coupée en 2 morceaux(le chiffre du bas).

Consigne:
Tenir collées les 2 moitiés de la pomme.

Ça fait une pomme complète. Les participants regardent de haut ces 2 moitiés qu'ils tiennent collées. Quelle image voient-ils cette fois? Ils voient encore le rond avec une coupure au milieu, verticalement. La formatrice dessine au tableau cette figure:

[Voir l'image pleine grandeur]

ou horizontalement

[Voir l'image pleine grandeur]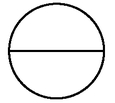

Alors chacun identifie le dessin de pomme qu'il voit devant lui. Elle désigne un côté, puis l'autre: ce côté-là, c'est une moitié, une demi-pomme. Ce côté-là aussi c'est une moitié, l'autre demi-pomme. Elle dessine aussi les moitiés prises séparément:

[Voir l'image pleine grandeur]

Évidemment, si vous avez dessiné la coupure horizontale, vous dessinez aussi ces figures:

[Voir l'image pleine grandeur]

Chaque participant exprime à quoi lui fait penser chacune de ces figures. Si on veut leur faire deviner l'addition de 2 demi-tasses et leur faire manipuler, il faut prévoir du temps supplémentaire. C'est une démarche intéressante(voir variante).
«Comment ça s'appellerait si on coupait encore en 2 les moitiés de pomme?»

Consigne:
Couper chaque moitié de pomme en 2 parties.

La formatrice aide à nouveau à couper des fractions relativement égales. Chaque morceau s'appelle un quart de pomme. Écriture au tableau de la fraction selon les 2 façons: ¼ et 1/4.

Ils prennent un quart de pomme dans leur main et nomment la fraction. «Combien y a-t-il de morceaux en tout? Combien y a-t-il de quarts dans une pomme? Quatre.» On fait le lien avec l'écriture de la fraction: 1 sur 4, c'est 1 morceau (chiffre du haut) quand la pomme est coupée en 4 morceaux(chiffre du bas).

Consigne:
Identifier sur sa tasse la fraction ¼ et remplir sa tasse jusqu'à la ligne de la fraction x¼ de la tasse.

On suit sensiblement la même démarche que pour les autres quantités de liquide.

Puis, on revient aux morceaux de pomme pour leur faire comprendre la fraction ¾ . «Comment s'appelle un morceau de pomme comme celui-là?» Un quart.

Consigne:
Mettre dans sa main 3 morceaux de "quart" de pomme.

Ce qu'ils ont dans leur main, c'est la fraction trois quarts qui s'écrit ¾ . On leur demande ce que le chiffre 3 signifie: 3 morceaux, ce que le chiffre 4 signifie: la pomme est coupée en 4 morceaux en tout. On insiste sur ce qu'ils entendent, les 2 mots de l'expression trois, quarts . Puis, ils collent ces 3 morceaux ensemble et voient l'image que ça donne en regardant de haut. La formatrice dessine au tableau les figures ainsi formées, selon la disposition de leurs morceaux:

[Voir l'image pleine grandeur]

Chacun identifie la figure ou le dessin que ses morceaux de pomme représentent. La formatrice leur suggère de tourner leurs morceaux, ça fait un autre dessin, qui est au tableau aussi. Elle peut aussi dessiner les mêmes formes, sans les lignes de coupure. C'est encore la même fraction de ¾.

[Voir l'image pleine grandeur]

On revient souvent avec le nom de la fraction: «Comment s'appelle la fraction que vous tenez dans vos mains?» Puis, «Comment s'appelle le petit morceau qui reste sur la table? Un quart. Qu'est-ce qui arriverait si on collait ce morceau-là, le "quart de pomme" avec les autres?»

Laissez-les deviner avant de le faire.

Ça fait la pomme complète. La formatrice dessine au tableau la figure de la pomme avec ses coupures.

[Voir l'image pleine grandeur]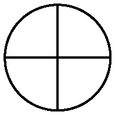

Quelle est la nouvelle fraction qu'on a maintenant? 1. C'est comme le 1 de une tasse. Il reste à mesurer ¾ de tasse d'eau colorée.

Consigne:
Identifier sur sa tasse la fraction ¾ et remplir sa tasse jusqu'à la ligne de cette fraction.

Même démarche.

Exercices écrits: no.1 et no.2

Exercice écrit: no.3
Avant de faire cette page, il faut avoir déjà vu les nombres fractionnaires, soit en atelier avec une démarche formelle, soit en l'expérimentant directement en cuisine. De toutes façons, il est bon d'en écrire quelques-uns avant de commencer l'exercice et de les expliquer: 1 ¼, 1 ¾, 2 ½, etc...

Les nombres fractionnaires sont difficiles à lire avec le mot tasse dans les recettes, parce qu'on doit dire 1 tasse et revenir en arrière pour lire la fraction et demie.

Variantes:

1. On refait le même atelier en mesurant du sel ou un autre ingrédient solide. On demande aux participants de brasser la tasse pour que la surface soit droite et vis-à-vis la ligne de la fraction.
2. Au lieu de couper des pommes, on coupe des oranges, des poires ou un autre fruit.
3. Fraction des figures: cercle, carré et rectangle. La formatrice prépare une image encerclée, avec des pointillés qui la découpent en quatre. N'importe quelle image peut faire l'affaire, à condition qu'elle touche les 4 parties.

Exercice écrit: no.4

On leur fait nommer la figure du contour: cercle ou rond. À quoi ça leur fait penser? Au dessin de la pomme coupée en 4, quand on la regarde de haut.

Consigne:
Découper le contour du cercle.

Quelle fraction ce dessin représente-t-il? Un bonhomme complet: 1. C'est comme quoi? Comme une pomme complète ou une tasse.

Consigne:
Découper le dessin en 4 parties, sur les pointillés.

On nomme chaque partie, on écrit la fraction ¼ .Puis on prend 2 parties qui se touchent, n'importe quelles. Ça serait vrai aussi si les quarts ne se touchaient pas, mais ça serait très difficile à comprendre.

Quelle fraction on obtient?

La réponse 2/4 est aussi juste que ½: 2 morceaux si le dessin est coupé en 4 morceaux. La formatrice dessine au tableau les figures ainsi obtenues. C'est la même chose que si on avait coupé le cercle en 2 parties et pris une partie. Ensuite, on prend 3 parties. On nomme la fraction, on l'écrit, on l'explique: 3 morceaux quand le dessin est coupé en 4 , etc...

C'est la même chose pour le dessin carré.

Exercice écrit: no.5

Si vous prenez une feuille 8%> x 11, les participants commencent par couper sur les lignes du haut et du bas pour obtenir un carré.

Même démarche pour chaque fraction.

Exercice écrit: no.6

Pour la figure du rectangle, vous utilisez une image haute et étroite. Vous tracez des pointillés à la mi-hauteur, au quart et au trois-quarts de la hauteur. Vous suivez la même démarche.

[Voir l'image pleine grandeur]

Nous n'avons pas eu l'occasion de le faire, mais ça aide sûrement à comprendre les fractions en hauteur sur la tasse à mesurer.

4. Addition de fractions. Quand on mesure l'eau colorée, on leur fait deviner ce qui va arriver si on transvide une demi-tasse avec une autre demi-tasse, ou n'importe quelle combinaison de fractions. Ensuite ils le font et vérifient leurs devinettes. Ils nomment la nouvelle fraction, l'écrivent, etc... On peut même leur faire écrire des additions de fractions.

Exemple:

[Voir l'image pleine grandeur]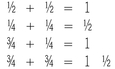

La même démarche peut se faire avec les morceaux de pommes et les dessins de figures.

5. Quand le groupe est prêt, même démarche avec les fractions 1/3 et 2/3.

Exercice 1

Nom: ___________

Combien y a-t-il d'eau dans la tasse à mesurer? Écris la fraction.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 2

Nom: ___________

Dessine l'eau dans la tasse selon la fraction.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 3

Nom: ___________

Combien y a-t-il de liquide dans la tasse à mesurer(ou les tasses)?
Découpe et colle la fraction dans la bonne case.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 4

Nom: ___________

Découpe le contour du cercle et sur les pointillés quand la formatrice le demande.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 5

Nom:___________

Découpe sur les 2 lignes noires et sur les point il lés quand la formatrice le demande.

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Exercice 6

Nom: ___________

Colorie la fraction demandée

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Liste aléatoire de matériel utilisé en calcul avec des adultes handicapés intellectuels

Alpha Math	Les Éditions Alpha Soleil
Arithmétique au jour le jour	(I.F.P.C.A.) C.S. De La Jonquière
Arithmétique fonctionnelle	G A A- 105 Éducation des adultes
Bingo (Le Trend) Monnaie, heures, achats	Bureau en gros
Boîte à outils pour compter	Centre Franco-Ontarien Renée Godbout
Étampes pièces de monnaie	Brault-Bouthillier Éditeur
Horloges individuelles	Brault-Bouthillier Éditeur
Je compte l'argent	Les Éditions Scolartek
La boîte à crayon 1 et 2	C.S. de Sherbrooke Service Éducatif (819-822-5300)
Les maths de la vie	Centre Franco-Ontarien
L'arithmétique de tous les jours	Groupe Populaire COMQUAT
Mathématiques(adultes) Mathématiques au quotidien	I.F.P.C.A. C.S. des Mille-Iles R.G.P.A.Q.
Monergo	Les Éditions Nouvelles
Paiement Comptant	C.S. St-Jérôme Centre Marchand
Passeport Mathématique 1-2-3-4	Les Éditions Trécarré
Résolution de problèmes Résolution de problèmes 1-2-3	Les Éditions de l'Envolée Les Éditions Marie-France
Mon livre de bord	Groupe Centre Lac d'Alma
Tambour Battant 3	Les Éditions Marie-France
Taratata	Les Éditions Marie-France
Véritec	Brault-Bouthillier
Les premiers jeux de Félix	Les Éditions Trapèze 300, rue Sicard Ste-Thérèse, Québec.J7E 5R7
Ani-Math en vacances	Les Éditions Trécarré
Compte mon histoire Mater les Maths Heure et température Résolution logique	Les Éditions à Reproduire " " "
Mon budget	L'ACELF de votre région
Carnet de nombres en lettres de 1 à 100	À construire: se fait de la même grandeur que le livret de chèques et se glisse bien avec le relevé de chèques.

Ressources informatiques

Calmenta Élémentaire mon cher watson Crapo Chaîne d'opérations Figures et formes Jeux de réflexions	Centre de recherches appliquées Pour ordinateur. Internet.
A.B.Cirque Plumo à la ferme	Production Micro-Intel et Jeux G.B.

Conclusion

Après nos 5 années d'ateliers de calcul et la réalisation de ce projet, nous sommes convaincues que le développement de la logique des nombres chez les adultes handicapés intellectuels est possible. Ce développement passe par la manipulation et sa symbolisation, par une gradation des difficultés et par un contenu créatif et ludique. Ce développement se fera à différents degrés selon le handicap de l'adulte.

Nous croyons qu'il peut être néfaste de considérer nos participants comme plafonnés. Ils le sont beaucoup moins qu'on pourrait le croire. Ils apprennent plus lentement, mais ils apprennent.

Si un participant remplit un cahier d'exercices page par page, sans manipuler, qu'est-ce qu'il va comprendre dans tout ça? Quand il aura de la difficulté , on va se contenter de dire qu'il est limité par son handicap?

Le projet "La danse des chiffres" a été pour nous l'occasion d'une remise en question: Qu'est-ce qui est important? Qu'ils soient heureux, qu'ils comprennent un peu mieux leur monde, leur environnement et qu'ils développent un peu plus d'autonomie dans leur quotidien: apprendre à cuisiner, à gérer des montants à leur disposition, etc.

Pour nous, ce qui est important aussi, c'est qu'ils vivent des succès et qu'ils sentent leur progrès. C'est à la fois une source de fierté pour eux et une importante motivation pour nous. Et pour vous, qu'est-ce qui est important?

Nous serions très heureuses de recevoir vos questions, commentaires et impressions. Merci.

Remerciements

Nous remercions sincèrement, les 16 enseignantes, enseignants et formatrices que nous avons rencontrés dans le cadre de ce projet. Ces personnes nous ont accordé généreusement leur temps. Leur collaboration a été appréciée.

Nous remercions de façon spéciale madame Bernadette Janvier, professeure à l'UQAM, qui est venue nous rencontrer. Ses conseils et son expertise ont été déterminants pour notre projet.

Merci à madame Diane Martin pour sa superbe illustration de la page couverture.

Finalement, merci à toute l'équipe de l'A.B.C. ainsi qu'à madame Lise Leduc, pour les lectures, commentaires et vérifications.

Références

ERMEL-INRP (1991). Nos conceptions de l'apprentissage et de l'enseignement in Apprentissages numériques et résolution de problèmes, Paris: Hatier 15-35*

Baroody, A J. (1991). Remédier aux difficultés courantes du comptage, Les chemins du nombre, Presses universitaires de Lille. Lille. 378-399*

Giroux, J (1992) Les relations entre les connaissances sur la suite des nombres et les opérations. Document de travail. UQAM*

Brissiaud, R. (1989). La numération et l'addition des nombres de 2 chiffres, in Comment les enfants apprennent à calculer. Retz, Paris.*

Monergo, gestion de l'argent, guide d'enseignement d'un scénario de paiement prudent. Caroline Drouin, Jacques Langevin, Caroline Germain, Sylvie Rocque. Éditions Nouvelles, Montréal, 1998.

• Textes tirés de ces ouvrages dans "Textes colligés, EDU-6795", préparé par Jacinthe Giroux, UQAM.
• Cassette vidéo(45 min. 53 sec)
  "Le concept de nombre et son acquisition chez le jeune enfant" 1987, Bednarz Nadine, Archambault Jacques, Janvier Bernadette, Montréal, UQAM, CIRADE. Service de l'audiovisuel.

Annexe 1 – Suggestions pour terminer un atelier quand ils sont fatigués

• Jeux de cartes comme la bataille.
• Jeu de bingo: Sur une page de nombres de 0 jusqu'à 100,(voir annexe)les participants placent des jetons sur les nombres que la formatrice dicte. Si les jetons sont transparents , on peut leur faire lire ces chiffres après.
  On peut aussi leur faire nommer chacun un nombre de leur choix pour que les autres le trouvent et placent un jeton.
• Jeu d'échelles et de serpents.
• Jeu de jour de paye.
• Jeu de «Jean dit» pour la latéralité (gauche droite).
• Jeu du sac de jetons: Les participants sont placés en cercle. Un participant compte les jetons d'un paquet, et les place dans un sac refermable. On fait circuler le sac d'un participant à l'autre. Au signal de la formatrice, le participant qui a le sac en mains devine combien il contient de jetons. Ensuite, il compte pour vérifier sa devinette. On l'applaudit s'il a raison. Puis, on change le nombre. La formatrice demande combien il y aura de jetons si on enlève 1, ou si on en ajoute 3, etc... On recompte pour vérifier. Le sac recommence à circuler, etc...(conservation du nombre).

Annexe 2 – Page de Bingo

0	1	2	3	4	5	6	7	8	9
10	11	12	13	14	15	16	17	18	19
20	21	22	23	24	25	26	27	28	29
30	31	32	33	34	35	36	37	38	39
40	41	42	43	44	45	46	47	48	49
50	51	52	53	54	55	56	57	58	59
60	61	62	63	64	65	66	67	68	69
70	71	72	73	74	75	76	77	78	79
80	81	82	83	84	85	86	87	88	89
90	91	92	93	94	95	96	97	98	99
100

Crédits

Conception, rédaction et traitement de texte
Hélène Patenaude
Madeleine Jean
Lise Duval

Comité lecture
Claudette Lacroix
Lise Duval

Lecture et correction d'épreuves
Pierrette Picotte
Claudette Lacroix
Lise Leduc
Lise Duval

Conception graphique et illustration
Diane Martin
Madeleine Jean
Lise Duval

L'A.B.C. des Manoirs, 2001

L'A.B.C. des Manoirs
568, Léon Martel
Terrebonne (Québec) J6W 2J8
Téléphone: (450) 471- 6928
Télecopieur: (450) 471- 9328
abcdesmanoirs@moncourrier.com

La réalisation de ce document a été rendu possible grâce à une subvention du programme initiatives fédérales-provinciales conjointes en alphabétisation (IFPCA) 2000-2001