Avis aux lecteur

L'emploi du masculin doit être entendu comme un neutre et n'a pas d'autres buts que d'alléger la présentation matérielle du texte

Présentation

Ce recueil de langage mathématique réfère au vocabulaire utilisé en formation de base (alphabétisation). Cependant, il peut être à l'usage de tous par son contenu notionnel thématique.

La définition et la compréhension des termes utilisés faciliteront la bonne application des résolutions de problèmes proposées en classe et dans la vie de tous les jours.

Les diverses compétences acquises permettront le transfert de celles-ci et donneront plus d'autonomie.

Que ce document devienne un guide d'accompagnement pour la réussite des mathématiques.

[Voir l'image pleine grandeur]

Chapitre 1 – L'orientation spatiale et temporelle

[Voir l'image pleine grandeur]

A. La position dans l'espace

[Voir l'image pleine grandeur]

1. Espace : étendue indéfinie qui contient et entoure tous les objets

[Voir l'image pleine grandeur]

2. À droite de : côté opposé à celui du cœur, l'opposé de gauche

[Voir l'image pleine grandeur]

3. À gauche de : l'opposé de droite

[Voir l'image pleine grandeur]

4. Opposé : mettre vis-à-vis, comparer

[Voir l'image pleine grandeur]

5. Entre : entre deux éléments

[Voir l'image pleine grandeur]

6. En haut de : endroit plus élevé, au-dessus de

[Voir l'image pleine grandeur]

7. En bas de : partie inférieure, au-dessous de

[Voir l'image pleine grandeur]

8. Avant : précède

[Voir l'image pleine grandeur]

9. Après : à la suite

[Voir l'image pleine grandeur]

10. Centre : milieu d'un espace

[Voir l'image pleine grandeur]

11. Ligne horizontale :

[Voir l'image pleine grandeur]

12. Ligne verticale :

[Voir l'image pleine grandeur]

13. Ligne oblique :

[Voir l'image pleine grandeur]

B. Les données de base pour le temps

[Voir l'image pleine grandeur]

1 minute = 60 secondes
1/4 heure = 15 minutes
1/2 heure = 30 minutes
3/4 heure = 45 minutes
1 heure = 60 minutes
1 journée = 24 heures
1 jour = quotidien
1 semaine = 7 jours
1 semaine = hebdomadaire
1 mois = 4 semaines
1 mois = mensuel
1 année = 365 jours
1 année = 52 semaines
1 année = 12 mois
1 année = annuel
1 siècle = 100 ans

C. Le temps dans le système international

1. La date s'écrit selon le système international dans l'ordre suivant :
L'année, le mois, le jour : 1985 08 10 / 1985-08-10 (10 août 1985)Pour séparer l'année, le mois et le jour, tu peux laisser un espace ou utiliser des tirets
Pour la date, un chiffre plus petit que dix (10) doit être précédé d'un zéro
Ex. : le 8 mai 1986 s'écrit 1986-05-08

[Voir l'image pleine grandeur]

2. Les heures s'écrivent selon le système international dans l'ordre suivant :
L'heure, la minute, la seconde : 16 : 30 : 58 (16 h 30 min 58 s)

[Voir l'image pleine grandeur]

• Pour l'heure, on utilise le système 24 heures
  À partir de midi, tu additionnes 12 au nombre indiqué par la petite aiguille
  Ex. : 4 heures de l'après-midi (p.m.) devient 16 heures
  04:00 + 12:00 = 16:00
  4 h + 12 h = 16 h
• Pour les minutes, tu multiplies par 5 le nombre indiqué par la grande aiguille
  Ex. : le chiffre 10 X 5 = 50 minutes

[Voir l'image pleine grandeur]

Tableau des symboles
Heure	h
Minute	min
Seconde	s

Chapitre 2 – Les nombres naturels

[Voir l'image pleine grandeur]

A. Les chiffres

1	Arabes	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
2	A rebours (sens inverse)	9, 8, 7, 6, 5, 4, 3, 2, 1, 0
3	Servent à faire des nombres	13, 24, 55, 79, 142, 523, etc.
4	Romains	I	II	III	IV	V	VI	VII	VIII	IX	X	L	C	D	M
		1	2	3	4	5	6	7	8	9	10	50	100	500	1000
5	Réfèrent	Quantité, date, heure, âge, page, argent, numéro d'ordre, adresse, loi, téléphone, etc.

B. Les nombres

1. Composés de deux chiffres et plus

2. Écrits en chiffres ou en lettres avec ou sans trait d'union (tableau page 7)

3. S'appellent adjectifs numéraux (2 sortes)

• Cardinaux : tous les nombres
• Ordinaux :
  - Indiquent le rang dont premier (1^er) et dernier
  - Nombres auxquels on a ajouté «ième» (suffixe) Ex. : troisième (3^ième), vingtième (20^ième)
  - «Second» est employé à la place de «deuxième» seulement quand il y a deux éléments
  - Croissants : du plus petit au plus grand en ordre (<)
  - Décroissants : du plus grand au plus petit en ordre (>)
  - Pairs : se terminent par 0, 2, 4, 6, 8, toujours divisibles par 2
  - Impairs : se terminent par 1, 3, 5, 7, 9

4. Tableau des nombres écrits en lettres¹

1	un	11	onze			21	vingt-et-un			31	trente-et-un
2	deux	12	douze			22	vingt-deux			32	trente-deux
3	trois	13	treize			23	vingt-trois			33	trente-trois
4	quatre	14	quatorze			24	vingt-quatre			34	trente-quatre
5	cinq	15	quinze			25	vingt-cinq			35	trente-cinq
6	six	16	seize			26	vingt-six			36	trente-six
7	sept	17	dix-sept			27	vingt-sept			37	trente-sept
8	huit	18	dix-huit			28	vingt-huit			38	trente-huit
9	neuf	19	dix-neuf			29	vingt-neuf			39	trente-neuf
10	dix	20	vingt			30	trente			40	Quarante
41	quarante-et-un			51	cinquante-et-un			61	soixante-et-un
42	quarante-deux			52	cinquante-deux			62	soixante-deux
43	quarante-trois			53	cinquante-trois			63	soixante-trois
44	quarante-quatre			54	cinquante-quatre			64	soixante-quatre
45	quarante-cinq			55	cinquante-cinq			65	soixante-cinq
46	quarante-six			56	cinquante-six			66	soixante-six
47	quarante-sept			57	cinquante-sept			67	soixante-sept
48	quarante-huit			58	cinquante-huit			68	soixante-huit
49	quarante-neuf			59	cinquante-neuf			69	soixante-neuf
50	cinquante			60	soixante			70	soixante-dix
71	soixante-et-onze			81	quatre-vingt-un			91	quatre-vingt-onze
72	soixante-douze			82	quatre-vingt-deux			92	quatre-vingt-douze
73	soixante-treize			83	quatre-vingt-trois			93	quatre-vingt-treize
74	soixante-quatorze			84	quatre-vingt-quatre			94	quatre-vingt-quatorze
75	soixante-quinze			85	quatre-vingt-cinq			95	quatre-vingt-quinze
76	soixante-seize			86	quatre-vingt-six			96	quatre-vingt-seize
77	soixante-dix-sept			87	quatre-vingt-sept			97	quatre-vingt-dix-sept
78	soixante-dix-huit			88	quatre-vingt-huit			98	quatre-vingt-dix-huit
79	soixante-dix-neuf			89	quatre-vingt-neuf			99	quatre-vingt-dix-neuf
80	quatre-vingts			90	quatre-vingt-dix			100	cent, cent-un, etc

5. Les nombres premiers

5.1 C'est un nombre qui se divise «seulement» par «1» et par lui-même
Ex. : 5 ÷ 1 = 5
5 ÷ 5 = 1

5.2 Si le nombre peut se diviser par d'autres nombres, que 1 et lui-même, ce n'est pas un nombre premier
Ex. : 24 ÷ 6 = 4 ≠ un nombre premier

5.3 Tableau

Nombres premiers
2	3	5	7	11	13	17	19	23	29	31	37	41
43	47	53	59	61	67	71	73	79	83	89	97	101
103	107	109	113	127	131	137	139	149	151	157	163	167
173	179	181	191	193	197	199	211	223	227	229	233	239
241	251	257	263	269	271	277	281	283	293	307	311	313
317	331	337	347	349	353	359	367	373	379	383	389	397
401	409	419	421	431	433	439	443	449	457	461	463	467
479	487	491	499	503	509	521	523	541	547	557	563	569
571	577	587	593	599	601	607	613	617	619	631	641	…

C. Les symboles de comparaison

1. «<» signifie est «plus petit que». Ex. : (2 < 3)
La pointe du symbole est toujours vers le plus petit nombre. Ex. : (1 < 2); (33 < 34)

2. «>» signifie est «plus grand que»
La grande ouverture est toujours vers le plus grand nombre. Ex. : (4 > 3); (55 > 54)

3. «=» signifie est «égal à». Ex. : (2 = 2), (3 = 3) ou le ou la même que

4. «<» signifie est «inférieur (plus petit) ou égal à» Ex. : 6 < 7; 7 < 7; 0, 1, 2, 3, 4, 5, 6, 7 < 7

5. «>» signifie est «supérieur (plus grand) ou égal à»
Ex. : 8 > 7; 8 > 8; 8 > 0, 1, 2, 3, 4, 5, 6, 7, 8

D. La valeur de certains nombres naturels positifs

[Voir l'image pleine grandeur]

1. Le zéro (0) : valeur nulle : le seul nombre qui est à la fois + ou -
2. L'unité (1) : un
3. La dizaine (10) : dix (10 unités ou 10 doigts)
4. La douzaine (12) : douze (12 unités ou 12 œufs)
5. La centaine (100) : cent (groupe de 100 unités ou de 10 dizaines)
6. L'unité de mille (1 000) : mille (groupe de 1000 unités ou de 10 centaines)
7. La dizaine de mille (10 000) : dix mille (10 000 unités ou 100 centaines)
8. La centaine de mille (100 000) : cent mille (100 000 unités ou 1 000 centaines)
9. Le million (1 000 000) : un million : (1 000 000 unités ou 10 000 centaines)
10. Etc.

[Voir l'image pleine grandeur]

E. Les symboles et la valeur de «l'argent»

1. Les symboles
Le signe «¢» signifie cent
Le signe «$» signifie dollar

[Voir l'image pleine grandeur]

• Ces symboles de l'unité monétaire se placent après le nombre sur la même ligne. Ex. : 4,25$
• Les cents et les dollars sont séparés par une virgule que tu dois toujours abaisser quelle que soit l'opération (+ ou -) (x ou -=-). Ex. : 10,30$
• La notation décimale est utilisée dans notre système monétaire et doit se limiter à deux chiffres après la virgule. Ex. : 5,35$

2. La valeur

2.1 Les pièces de monnaie

• 0,01$ ou 1¢
• 0,05$ ou 5¢
• 0,10$ ou 10¢
• 0,25$ ou 25¢
• 1,00$ ou 100¢
• 2,00$ ou 200¢

2.2. Les billets- 5,00$

• 10,00$
• 20,00$
• 50,00$
• 100,00$

Remarque : tu peux garder la même valeur en échangeant différents billets ou pièces de monnaie. Ex. : 5,00$ en monnaie = 5,00$ en billet

[Voir l'image pleine grandeur]

3. Les documents (paiements ou preuves)
Le chèque : papier officiel d'une banque ou d'une caisse qui remplace l'argent (le modèle peut varier selon l'institution financière)

Éléments mathématiques du chèque

(1) Date (toujours écrite en chiffres)
(2) Personne à qui l'on fait le chèque
(3) Le montant en lettres précédé et suivi d'un trait auquel on ajoute le montant en monnaie qui s'écrit en chiffres au bout de la ligne
(4) Le montant en argent
(5) Numéro du folio (compte) (n°)
(6) Numéro du chèque
(7) La signature de la personne qui paie
(8) La raison du chèque
(9) Identification personnelle (personne qui fait le chèque)

Remarque : on le fait toujours au crayon à l'encre (stylo) sauf à l'encre rouge

[Voir l'image pleine grandeur]

Le reçu : pièce justificative
preuve écrite par laquelle une personne reconnaît avoir reçu une somme d'argent à titre de paiement, de prêt ou de dépôt

(1) Date (toujours écrite en chiffres)
(2) Personne à qui l'on fait le reçu
(3) Le montant en lettres
(4) Le montant en argent
(5) La signature de la personne qui reçoit le paiement
(6) Identification personnelle (personne qui fait le reçu)
Remarque : on le fait toujours au crayon à l'encre (stylo) sauf à l'encre rouge

[Voir l'image pleine grandeur]

4. Les opérations financières

• débit : retrait au compte (-)
• crédit : dépôt au compte (+)
• solde : différence entre le crédit (+) et le débit (-)

Ne pas utiliser le mot «balance» Ce qui reste : peut-être (+) ou (-)

F. La série à «compléter» en comptant par...

1. Par «deux» : faire des bonds de «2» ou ajouter «2»
2. Par «trois» : faire des bonds de «3» ou ajouter «3»
3. Par «quatre» faire des bonds de «4» ou ajouter «4»
4. Par «cinq» : faire des bonds de «5» ou ajouter «5»
5. Par «dix» : faire des bonds de «10» ou ajouter «10»
6. Par «vingt-cinq» : faire des bonds de «25» ou ajouter «25»
7. Etc.

[Voir l'image pleine grandeur]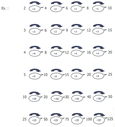

Chapitre 3 – Les quatre opérations + - ÷ x

[Voir l'image pleine grandeur]

A. La droite numérique

1. La définition :

• C'est une ligne graduée avec une série de nombres entiers en ordre croissant

[Voir l'image pleine grandeur]

• C'est un guide pour compter comme une règle ou un ruban à mesurer
• C'est une illustration de la multiplication à partir de l'addition

[Voir l'image pleine grandeur]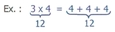

B. La colonne et le tableau

[Voir l'image pleine grandeur]

C. L'addition (plus, +)

1. Opération symbolisée par le signe +

2. Ajouter quelque chose

3. Augmenter

4. Trouver la somme, le résultat ou le total = réponse

5. Aller + retour (additionner deux fois)

6. En tout, au total, en entier, au complet

7. Retenue : chiffre reporté et ajouté dans la colonne suivante

[Voir l'image pleine grandeur]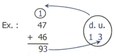

8. Table des additions (+)

Table des additions
1 + 1= 2 1 + 2= 3 1 + 3= 4 1 + 4= 5 1 + 5= 6 1 + 6= 7 1 + 7= 8 1 + 8= 9 1 + 9= 10 1 + 10= 11 1 + 11= 12 1 + 12= 13	2 + 1 = 3 2 + 2 = 4 2 + 3 = 5 2 + 4 = 6 2 + 5 = 7 2 + 6 = 8 2 + 7 = 9 2 + 8 = 10 2 + 9 = 11 2 + 10 = 12 2 + 11 = 13 2 + 12 = 14	3 + 1 = 4 3 + 2 = 5 3 + 3 = 6 3 + 4 = 7 3 + 5 = 8 3 + 6 = 9 3 + 7 = 10 3 + 8 = 11 3 + 9 = 12 3 + 10 = 13 3 + 11 = 14 3 + 12 = 15	4 + 1 = 5 4 + 2 = 6 4 + 3 = 7 4 + 4 = 8 4 + 5 = 9 4 + 6 = 10 4 + 7 = 11 4 + 8 = 12 4 + 9 = 13 4 + 10 = 14 4 + 11 = 15 4 + 12 = 16	5 + 1 = 6 5 + 2 = 7 5 + 3 = 8 5 + 4 = 9 5 + 5 = 10 5 + 6 = 11 5 + 7 = 12 5 + 8 = 13 5 + 9 = 14 5 + 10 = 15 5 + 11 = 16 5 + 12 = 17	6 + 1 = 7 6 + 2 = 8 6 + 3 = 9 6 + 4 = 10 6 + 5 = 11 6 + 6 = 12 6 + 7 = 13 6 + 8 = 14 6 + 9 = 15 6 + 10 = 16 6 + 11 = 17 6 + 12 = 18
7 + 1 = 8 7 + 2 = 9 7 + 3 = 10 7 + 4 = 11 7 + 5 = 12 7 + 6 = 13 7 + 7 = 14 7 + 8 = 15 7 + 9 = 16 7 + 10 = 17 7 + 11 = 18 7 + 12 = 19	8 + 1 = 9 8 + 2 = 10 8 + 3 = 11 8 + 4 = 12 8 + 5 = 13 8 + 6 = 14 8 + 7 = 15 8 + 8 = 16 8 + 9 = 17 8 + 10 = 18 8 + 11 = 19 8 + 12 = 20	9 + 1 = 10 9 + 2 = 11 9 + 3 = 12 9 + 4 = 13 9 + 5 = 14 9 + 6 = 15 9 + 7 = 16 9 + 8 = 17 9 + 9 = 18 9 + 10 = 19 9 + 11 = 20 9 + 12 = 21	10 + 1 = 11 10 + 2 = 12 10 + 3 = 13 10 + 4 = 14 10 + 5 = 15 10 + 6 = 16 10 + 7 = 17 10 + 8 = 18 10 + 9 = 19 10 + 10 = 20 10 + 11 = 21 10 + 12 = 22	11 + 1 = 12 11 + 2 = 13 11 + 3 = 14 11 + 4 = 15 11 + 5 = 16 11 + 6 = 17 11 + 7 = 18 11 + 8 = 19 11 + 9 = 20 11 + 10 = 21 11 + 11 = 22 11 + 12 = 23	12 + 1 = 13 12 + 2 = 14 12 + 3 = 15 12 + 4 = 16 12 + 5 = 17 12 + 6 = 18 12 + 7 = 19 12 + 8 = 20 12 + 9 = 21 12 + 10 = 22 12 + 11 = 23 12 + 12 = 24

[Voir l'image pleine grandeur]

D. La soustraction (moins, -)

1. Opération symbolisée par le signe -

2. Trouver le reste ou la différence entre 2 nombres en enlevant au premier la valeur du second = réponse

[Voir l'image pleine grandeur]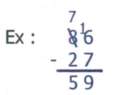

3. Enlever

4. Ôter

5. De moins que (-)

6. De plus que (-)
Ex. : Luc a 5,00$ et Line a 2,00$. Combien Luc a-t-il de plus que Line? 5,00$ - 2,00$ = 3,00$

7. Combien : Me manque-t-il?, Il me reviendra (remise)?, Ai-je perdu?, Reste-t-il?, etc.

8. Déduction : retrancher, enlever

9. Profit : différence entre gain et perte

10. Emprunt : quantité prélevée à une autre valeur supérieure à celle demandée (dizaine, centaine, etc.)

11. Écart (-) : différence entre deux nombres

12. Le salaire brut et le salaire net (-)

13. La ou les retenue(s) sur un montant brut ou sur un tout (-)

14. Le plus élevé (-), le plus cher (-), quand on veut la différence

15. Table des soustractions (-)

Table des soustractions
1 - 1 = 0 2 - 1 = 1 3 - 1 = 2 4 - 1 = 3 5 - 1 = 4 6 - 1 = 5 7 - 1 = 6 8 - 1 = 7 9 - 1 = 8 10 - 1 = 9 11 - 1 = 10 12 - 1 = 11	2 - 2 = 0 3 - 2 = 1 4 - 2 = 2 5 - 2 = 3 6 - 2 = 4 7 - 2 = 5 8 - 2 = 6 9 - 2 = 7 10 - 2 = 8 11 - 2 = 9 12 - 2 = 10 13 - 2 = 11	3 - 3 = 0 4 - 3 = 1 5 - 3 = 2 6 - 3 = 3 7 - 3 = 4 8 - 3 = 5 9 - 3 = 6 10 - 3 = 7 11 - 3 = 8 12 - 3 = 9 13 - 3 =10 14 - 3 = 11	4 - 4 = 0 5 - 4 = 1 6 - 4 = 2 7 - 4 = 3 8 - 4 = 4 9 - 4 = 5 10 - 4 = 6 11 - 4 = 7 12 - 4 = 8 13 - 4 = 9 14 - 4 = 10 15 - 4 = 11	5 - 5 = 0 6 - 5 = 1 7 - 5 = 2 8 - 5 = 3 9 - 5 = 4 10 - 5 = 5 11 - 5 = 6 12 - 5 = 7 13 - 5 = 8 14 - 5 = 9 15 - 5 = 10 6 - 5 = 11	6 - 6 = 0 7 - 6 = 1 8 - 6 = 2 9 - 6 = 3 10 - 6 = 4 11 - 6 = 5 12 - 6 = 6 13 - 6 = 7 14 - 6 = 8 15 - 6 = 9 16 - 6 = 10 17 - 6 = 11
7 - 7 = 0 8 - 7 = 1 9 - 7 = 2 10 - 7 = 3 11 - 7 = 4 12 - 7 = 5 13 - 7 = 6 14 - 7 = 7 15 - 7 = 8 16 - 7 = 9 17 - 7 = 10 18 - 7 = 11	8 - 8 = 0 9 - 8 = 1 10 - 8 = 2 11 - 8 = 3 12 – 8 = 4 13 - 8 = 5 14 - 8 = 6 15 - 8 = 7 16 - 8 = 8 17 - 8 = 9 18 - 8 = 10 19 - 8 = 11	9 - 9 = 0 10 - 9 = 1 11 - 9 = 2 12 - 9 = 3 13 - 9 = 4 14 - 9 = 5 15 - 9 = 6 16 - 9 = 7 17 - 9 = 8 18 - 9 = 9 19 - 9 = 10 20 - 9 = 11	10 - 10 = 0 11 - 10 = 1 12 - 10 = 2 13 - 10 = 3 14 - 10 = 4 15 - 10 = 5 16 - 10 = 6 17 - 10 = 7 18 - 10 = 8 19 - 10 = 9 20 - 10 = 10 21 - 10 = 11	11 - 11 = 0 12 - 11 = 1 13 - 11 = 2 14 - 11 = 3 15 - 11 = 4 16 - 11 = 5 17 - 11 = 6 18 - 11 = 7 19 - 11 = 8 20 - 11 = 9 21 - 11 = 10 22 - 11 = 11	12 - 12 = 0 13 - 12 = 1 14 - 12 = 2 15 - 12 = 3 16 - 12 = 4 17 - 12 = 5 18 - 12 = 6 19 - 12 = 7 20 - 12 = 8 21 - 12 = 9 22 - 12 = 10 23 - 12 = 11

[Voir l'image pleine grandeur]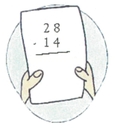

E. La multiplication (fois, X)

1. Opération symbolisée par le signe X

2. Multiplier par...

3. Addition répétée : la multiplication permet de remplacer la répétition de l'addition.
Ex. : (3 X 5) = (5 + 5 + 5)

4. Termes de la multiplication :
Multiplicande : le premier facteur que l'on X
Multiplicateur : le deuxième facteur que l'on X
Produit : réponse. Ex. : 5 X 3 = 15

Facteur multiplicande X facteur multiplicateur = produit
5 X 3 = 15

5. L'argent est toujours le premier facteur (multiplicande) dans la X et les objets sont toujours deuxième facteur (multiplicateur) à insérer. Ex. : 5,35$ x 2 = 10,70$

6. Fois plus (X)

7. Propriétés
Tous les nombres X par 0 = 0
Ex. : 8 X 0 = 0
241 X 0 = 0
Tous les nombres X par 1 = nombre multiplié
Ex. : 8 X 1 = 8
241 X 1 = 241
8. Le montant donné à l'heure (ex. : 10,00$/heure)

• Temps simple = montant donné à l'heure (10,00$ X 1) = 10,00$
• Temps et demi = montant donné à l'heure X par 1,5 ou 1 ½
  (10,00$ X 1,5) = 15,00$
• Temps double = montant donné à l'heure X par 2 (10,00$ X 2) = 20,00$

9. Table de multiplications (X)

Table des multiplications
1 X 1 = 1 1 X 2 = 2 1 X 3 = 3 1 X 4 = 4 1 X 5 = 5 1 X 6 = 6 1 X 7 = 7 1 X 8 = 8 1 X 9 = 9 1 X 10 = 10 1 X 11 = 11 1 X 12 = 12	2 X 1 = 2 2 X 2 = 4 2 X 3 = 6 2 X 4 = 8 2 X 5 = 10 2 X 6 = 12 2 X 7 = 14 2 X 8 = 16 2 X 9 = 18 2 X 10 = 20 2 X 11 = 22 2 X 12 = 24	3 X 1 = 3 3 X 2 = 6 3 X 3 = 9 3 X 4 = 12 3 X 5 = 15 3 X 6 = 18 3 X 7 = 21 3 X 8 = 24 3 X 9 = 27 3 X 10 = 30 3 X 11 = 33 3 X 12 = 36	4 X 1 = 4 4 X 2 = 8 4 X 3 = 12 4 X 4 = 16 4 X 5 = 20 4 X 6 = 24 4 X 7 = 28 4 X 8 = 32 4 X 9 = 36 4 X 10 = 40 4 X 11 = 44 4 X 12 = 48	5 X 1 = 5 5 X 2 = 10 5 X 3 = 15 5 X 4 = 20 5 X 5 = 25 5 X 6 = 30 5 X 7 = 35 5 X 8 = 40 5 X 9 = 45 5 X 10 = 50 5 X 11 = 55 5 X 12 = 60	6 X 1 = 6 6 X 2 = 12 6 X 3 = 18 6 X 4 = 24 6 X 5 = 30 6 X 6 = 36 6 X 7 = 42 6 X 8 = 48 6 X 9 = 54 6 X 10 = 60 6 X 11 = 66 6 X 12 = 72
7 X 1 = 7 7 X 2 = 14 7 X 3 = 21 7 X 4 = 28 X 5 = 35 7 X 6 = 42 7 X 7 = 49 7 X 8 = 56 7 X 9 = 63 7 X 10 = 70 7 X 11 = 77 7 X 12 = 84	8 X 1 = 8 8 X 2 = 16 8 X 3 = 24 8 X 4 = 32 8 X 5 = 40 8 X 6 = 48 8 X 7 = 56 8 X 8 = 64 8 X 9 = 72 8 X 10 = 80 8 X 11 = 88 8 X 12 = 96	9 X 1 = 9 9 X 2 = 18 9 X 3 = 27 9 X 4 = 36 9 X 5 = 45 9 X 6 = 54 9 X 7 = 63 9 X 8 = 72 9 X 9 = 81 9 X 10 = 90 9 X 11 = 99 9 X 12 = 108	10 X 1 = 10 10 X 2 = 20 10 X 3 = 30 10 X 4 = 40 10 X 5 = 50 10 X 6 = 60 10 X 7 = 70 10 X 8 = 80 10 X 9 = 90 10 X 10 = 100 10 X 11 = 110 10 X 12 = 120	11 X 1 = 11 11 X 2 = 22 11 X 3 = 33 11 X 4 = 44 11 X 5 = 55 11 X 6 = 66 11 X 7 = 77 11 X 8 = 88 11 X 9 = 99 11 X 10 = 110 11 X 11 = 121 11 X 12 = 132	12 X 1 = 12 12 X 2 = 24 12 X 3 = 36 12 X 4 = 48 12 X 5 = 60 12 X 6 = 72 12 X 7= 84 12 X 8 = 96 12 X 9 = 108 12 X 10 = 120 12 X 11 = 132 12 X 12 = 144

[Voir l'image pleine grandeur]

10. Tableau des facteurs

4	1,2,4	55	1,5,11,55
6	1,2,3,6 56	56	1,2,4,7,8,14,28,56
8	1,2,4,8 57	57	1,3,19,57
9	1,3,9	58	1,2,29,58
10	1,2,5,10	60	1,2,3,4,5,6,10,12,15,20,30,60
12	1,2,3,4,6,12	62	1,2,31,62
14	1,2,7,14	63	1,3,7,9,21,63
15	1,3,5,15	64	1,2,4,8,16,32,64
16	1,2,4,8,16	65	1,5,13,65
18	1,2,3,6,9,18	66	1,2,3,6,11,22,33,66
20	1,2,4,5,10,20	68	1,2,4,17,34,68
21	1,3,7,21	69	1,3,23,69
22	1,2,11,22	70	1,2,5,7,10,14,35,70
24	1,2,3,4,6,8,12,24	72	1,2,3,4,6,8,9,12,18,24,36,72
25	1,5,25	74	1,2,37,74
26	1,2,13,26	75	1,3,5,15,25,75
27	1,3,9,27	76	1,2,4,19,38,76
28	1,2,4,7,14,28	77	1,7,11,77
30	1,2,3,5,6,10,15,30	78	1,2,3,6,13,26,39,78
32	1,2,4,8,16,32	80	1,2,4,5,8,10,16,20,40,80
33	1,3,11,33	81	1,3,9,27,81
34	1,2,17,34	82	1,2,41,82
35	1,5,7,35	84	1,2,3,4,6,7,12,14,21,28,42,84
36	1,2,3,4,6,9,12,18,36	85	1,5,17,85
38	1,2,19,38	86	1,2,43,86
39	1,3,13,39	87	1,3,29,87
40	1,2,4,5,8,10,20,40	88	1,2,4,8,11,22,44,88
42	1,2,3,6,7,14,21,42	90	1,2,3,5,6,9,10,15,18,30,45,90
44	1,2,4,11,22,44 91	91	1,7,13,91
45	1,3,5,9,15,45	92	1,2,4,23,46,92
46	1,2,23,46	93	1,3,31,93
48	1,2,3,4,6,8,12,16,24,48	94	1,2,47,94
49	1,7,49	95	1,5,19,95
50	1,2,5,10,25,50	96	1,2,3,4,6,8,12,16,24,32,48,96
51	1,3,17,51	98	1,2,7,14,49,98
52	1,2,4,13,26,52	99	1,3,9,11,33,99
54	1,2,3,6,9,18,27,54	100	1,2,4,5,10,20,25,50,100

F. La division (divisé par, ÷)

1. Opération symbolisée par le signe ÷

2. Diviser par : action de partager un tout en un certain nombre de parties d'égale valeur

3. Termes de la division :

• Le dividende : c'est le plus grand nombre, le nombre à diviser
• Le diviseur : c'est le nombre qui divise
• Quotient : réponse. Ex. : 8 + 4 = 2

Dividende ÷ diviseur = quotient
8 ÷ 4 =2

4. Fois moins (÷)
Ex. : Luc remplit 14 paniers de pommes par jour. Line en ramasse deux fois moins que Luc. Combien Line a-t-elle de paniers? 14 ÷ 2 = 7

5. Les propriétés

• Tous les nombres divisés par 0 = 0. Ex. : 8 ÷ 0 = 0
• Tous les nombres divisés par 1 = le nombre divisé. Ex. : 8 ÷ 1 = 8
• Tous les nombres divisés par eux-mêmes = 1. Ex. : 8 ÷ 8 = 1

6. Combien y en a-t-il dans? (÷)

7. La moyenne

• C'est additionner toutes les données que tu dois ensuite diviser par le nombre de données

[Voir l'image pleine grandeur]

8. Table de divisions (÷)

Table de divisions
1 ÷ 1 = 1 2 ÷ 1 = 2 3 ÷ 1 = 3 4 ÷ 1 = 4 5 ÷ 1 = 5 6 ÷ 1 = 6 7 ÷ 1 = 7 8 ÷ 1 = 8 9 ÷ 1 = 9 10 ÷ 1 = 10 11 ÷ 1 = 11 12 ÷ 1 = 12	2 ÷ 2 = 1 4 ÷ 2 = 2 6 ÷ 2 = 3 8 ÷ 2 = 4 10 ÷ 2 = 5 12 ÷ 2 = 6 14 ÷ 2 = 7 16 ÷ 2 = 8 18 ÷ 2 = 9 20 ÷ 2 = 10 22 ÷ 2 = 11 24 ÷ 2 = 12	3 ÷ 3 = 1 6 ÷ 3 = 2 9 ÷ 3 = 3 12 ÷ 3 = 4 15 ÷ 3 = 5 18 ÷ 3 = 6 21 ÷ 3 = 7 24 ÷ 3 = 8 27 ÷ 3 = 9 30 ÷ 3 = 10 33 ÷ 3 = 11 36 ÷ 3 = 12	4 ÷ 4 = 1 8 ÷ 4 = 2 12 ÷4 = 3 16 ÷ 4 = 4 20 ÷ 4 = 5 24 ÷ 4 = 6 28 ÷ 4 = 7 32 ÷ 4 = 8 36 ÷ 4 = 9 40 ÷ 4 = 10 44 ÷ 4 = 11 48 ÷ 4 = 12	5 ÷ 5 = 1 10 ÷ 5 = 2 15 ÷ 5 = 3 20 ÷ 5 = 4 25 ÷ 5 = 5 30 ÷ 5 = 6 35 ÷ 5 = 7 40 ÷ 5 = 8 45 ÷ 5 = 9 50 ÷ 5 = 10 55 ÷ 5 = 11 60 ÷ 5 = 12	6 ÷ 6 = 1 12 ÷ 6 = 2 18 ÷ 6 = 3 24 ÷ 6 = 4 30 ÷ 6 = 5 36 ÷ 6 = 6 42 ÷ 6 = 7 48 ÷ 6 = 8 54 ÷ 6 = 9 60 ÷ 6 = 10 66 ÷ 6 = 11 72 ÷ 6 = 12
7 ÷ 7 = 1 14 ÷ 7 = 2 21 ÷ 7 = 3 28 ÷ 7 = 4 35 ÷ 7 = 5 42 ÷ 7 = 6 49 ÷ 7 = 7 56 ÷ 7 = 8 63 ÷ 7 = 9 70 ÷ 7 = 10 77 ÷ 7 = 11 84 ÷ 7 = 12	8 ÷ 8 = 1 16 ÷ 8 = 2 24 ÷ 8 = 3 32 ÷ 8 = 4 40 ÷ 8 = 5 48 ÷ 8 = 6 56 ÷ 8 = 7 64 ÷ 8 = 8 72 ÷ 8 = 9 80 ÷ 8 = 10 88 ÷ 8 = 11 96 ÷ 8 = 12	9 ÷ 9 = 1 18 ÷ 9 = 2 27 ÷ 9 = 3 36 ÷ 9 = 4 45 ÷ 9 = 5 54 ÷ 9 = 6 63 ÷ 9 = 7 72 ÷ 9 = 8 81 ÷ 9 = 9 90 ÷ 9 = 10 99 ÷ 9 = 11 108 ÷ 9 = 12	10 ÷ 10 = 1 20 ÷ 10 = 2 30 ÷ 10 = 3 40 ÷ 10 = 4 50 ÷ 10 = 5 60 ÷ 10 = 6 70 ÷ 10 = 7 80 ÷ 10 = 8 90 ÷ 10 = 9 100 ÷ 10 = 10 110 ÷ 10 = 11 120 ÷ 10 = 12	11 ÷ 11 = 1 22 ÷ 11 = 2 33 ÷ 11 = 3 44 ÷ 11 = 4 55 ÷ 11 = 5 66 ÷ 11 = 6 77 ÷ 11 = 7 88 ÷ 11 = 8 99 ÷ 11 = 9 110 ÷ 11 = 10 121 ÷ 11 = 11 132 ÷ 11 = 12	12 ÷ 12 = 1 24 ÷ 12 = 2 36 ÷ 12 = 3 48 ÷ 12 = 4 60 ÷ 12 = 5 72 ÷ 12 = 6 84 ÷ 12 = 7 96 ÷ 12 = 8 108 ÷ 12 = 9 120 ÷ 12 = 10 132 ÷ 12 = 11 144 ÷ 12 = 12

G. La vérification des réponses pour les quatre opérations (la preuve)

1. Les opérations contraires

1.1 L'addition et la soustraction

1.2 La multiplication et la division

2. Inverser les opérations effectuées à partir du résultat obtenu

[Voir l'image pleine grandeur]

Chapitre 4 – Les fractions

[Voir l'image pleine grandeur]

A. La définition d'une fraction

C'est la représentation d'un nombre plus petit qu'une unité (1)

B. Les termes d'une fraction

1. L'expression écrite

[Voir l'image pleine grandeur]

2. La fraction ordinaire
C'est une partie d'un tout ou un morceau d'un objet séparé en parties égales2.2 Le numérateur indique :

• La ou les parties placée(s) au-dessus de la ligne horizontale ou oblique (barre de fraction) et en combien de parties égales se compose la fraction. Ex. : 1/2, le numérateur est «1»
  2.3 Le dénominateur indique
• Le tout placé au-dessous de la ligne horizontale ou oblique (barre de fraction)

[Voir l'image pleine grandeur]

• En combien de parties égales est divisé l'entier
  Remarque : pour les opérations de fractions, la barre de fraction doit demeurer un trait horizontal

[Voir l'image pleine grandeur]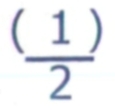

2.4 Dénominateur commun : nécessaire pour comparer les fractions entre elles, pour les additionner et pour les soustraire seulement

2.5 Le tout d'une fraction égale la partie nommée au dénominateur

[Voir l'image pleine grandeur]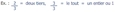

[Voir l'image pleine grandeur]

2.6 La grandeur des fractions ordinaires

• Avec le même numérateur
  - La plus grande fraction est celle qui a le + petit dénominateur

[Voir l'image pleine grandeur]

- La plus petite fraction est celle qui a le + grand dénominateur

[Voir l'image pleine grandeur]

• Avec le même dénominateur
  - La plus petite fraction est celle qui a le + petit numérateur

[Voir l'image pleine grandeur]

- La plus grande fraction est celle qui a le + grand numérateur

[Voir l'image pleine grandeur]

2.7. L'entier
- Représente tout l'objet ou un groupe

[Voir l'image pleine grandeur]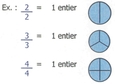

Remarque : le numérateur et le dénominateur sont identiques (pareils) dans les fractions pour avoir un entier

3. Les nombres fractionnaires
Un nombre entier accompagné d'une fraction
Ex. : 3 2/5 (la fraction «2/5» est ajoutée au nombre entier «3»)

4. Les expressions fractionnaires
Une fraction où le numérateur est plus grand ou égal au dénominateur
Ex. : 5/2 le numérateur «5» est plus grand que 2
6/6 = expression fractionnaire

5. Les fractions équivalentes

• Représentent la même partie d'un tout
• Réduites à la plus simple expression

5.1 C'est multiplier le numérateur et le dénominateur par le même chiffre afin d'exprimer un même rapport

[Voir l'image pleine grandeur]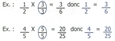

5.2 Si le produit croisé de deux fractions est identique, ces deux fractions sont alors équivalentes

[Voir l'image pleine grandeur]

5.3 Le plus petit commun multiple (PPCM)
Le dénominateur commun
C'est le plus petit nombre, différent de zéro, qui est multiple commun de deux ou de plusieurs nombres

[Voir l'image pleine grandeur]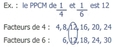

6. La simplification d'une fraction

6.1 C'est diviser le numérateur et le dénominateur par le même chiffre pour la rendre à sa plus simple expression

[Voir l'image pleine grandeur]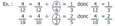

6.2 Chaque fois que tu divises un nombre par ce même nombre, le quotient est toujours égal à «1»

[Voir l'image pleine grandeur]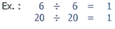

7. L'inversion d'une fraction
Dans la division des fractions seulementTu dois toujours inverser la fraction précédée du signe de la division pour ensuite faire une multiplication et obtenir le quotient

[Voir l'image pleine grandeur]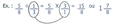

8. Les fractions d'heure
Les minutes sont parfois exprimées en fraction d'heure15 minutes = 1/4 d'heure

[Voir l'image pleine grandeur]

30 minutes = 1/2 heure

[Voir l'image pleine grandeur]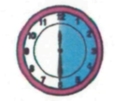

45 minutes = 3/4 d'heure

[Voir l'image pleine grandeur]

Chapitre 5 – Les nombres décimaux

[Voir l'image pleine grandeur]

A. La définition des nombres décimaux

[Voir l'image pleine grandeur]

Ce sont les chiffres qui viennent après la virgule dans l'écriture d'un nombre

B. L'emploi de la virgule

1. À droite de l'unité, après la virgule on écrit les dixièmes suivis des centièmes, des millièmes, des dix millièmes, etc.

2. La virgule se lit «et»
Ex. : 10,5 = dix et 5 dixièmes3. L'emploi de la virgule sert aussi

• À augmenter le nombre décimal en déplaçant vers la droite, d'une, de deux ou de trois positions et plus
  Ex. : 0,581 x 10 = 5,81
  0,581 x 100 = 58,1
  0,581 x 1000 = 581

4. Dans l'addition et la soustraction, il faut faire attention pour bien placer la virgule. Elle doit toujours être disposée dans les règles (ordre)

[Voir l'image pleine grandeur]

5. Tu limites généralement ta réponse à deux chiffres après la virgule

6. Dans la division, l'emploi de la virgule sert aussi à réduire ou diminuer le nombre décimal en se déplaçant vers la gauche d'une, de deux ou trois positions et plus
Ex. : 326,24 10 32,624
326,24 = 100 = 3,2624
326,24 + 1000 = 0,32624

7. Dans la multiplication, la virgule doit être bien placée dans le produit qui est la réponse de la multiplication. La somme des décimaux de tous les facteurs t'indique la position que tu dois donner à la virgule dans ta réponse

[Voir l'image pleine grandeur]

8. Tableau des nombres entiers et décimaux

[Voir l'image pleine grandeur]

• Se lit 478 millièmes

C. La valeur de position

La valeur de chaque chiffre dans un nombre décimal est déterminée par la «position» qu'il occupe dans ce nombre

• Le dixième (1/10)
• Le centième (1/100)
• Le millième (1/1000)

4/10 = 0,4	Un chiffre à droite de la virgule indique que le dénominateur de la fraction est 10
4/100 = 0,04	Deux chiffres à droite de la virgule indiquent que le dénominateur de la fraction est 100
4/1 000 = 0,004	Trois chiffres à droite de la virgule indiquent que le dénominateur de la fraction est 1 000

D. La fraction décimale

1. C'est l'autre forme pour écrire le nombre décimal (voir tableau précédent)

2. Peut être composée d'une partie entière et d'une partie décimale
Ex.: 1 4/10 = 1,4

3. Autres fractions décimales

• Une fraction ordinaire (2/5) et un nombre fractionnaire (1 2/5) doivent aussi être transformés en fractions décimales avant de devenir un nombre décimal

[Voir l'image pleine grandeur]

E. Le tableau des fractions décimales et des nombres décimaux

[Voir l'image pleine grandeur]

F. L'importance du «zéro»

1. Le «zéro» s'écrit toujours à gauche de la virgule s'il n'y a pas d'entier
Ex. : 0,16

2. Si le dernier chiffre de la décimale est un «zéro», il n'est pas nécessaire de l'indiquer. Cependant, l'ajout de plusieurs «zéro» à droite de la partie décimale ne change pas la valeur du nombre
Ex. : 2,050 = 2,05

G. La lecture du nombre décimal

1. Avec un nombre entier

• On lit la partie entière d'abord
• La virgule se lit «et»
• On lit la partie décimale en nommant la position du dernier chiffre
  Ex. : 13,81 = treize et quatre-vingt-un centième

2. Sans nombre entier

• On lit la partie décimale en nommant la position du dernier chiffre
  Ex. : 0,068 = soixante-huit millièmes

3. Les nombres décimaux sont ordonnés et peuvent se comparer avec les symboles : plus grand que (>), plus petit que (<) ou égal (=). Au besoin, on ajoutera un ou plusieurs «zéro»
Ex. : 11,42 et 11,5
On écrit : 11,42 et 11,50 (ajout d'un zéro)
On conclut : 11,42 < 11,5

H. La décomposition des nombres décimaux

1. La lecture se fait de gauche à droite en se servant du symbole de l'addition (+) pour séparer les nombres
Ex. : 14,78
1 dizaine + 4 unités + 7 dixièmes + 8 centièmes
ou =
14 unités + 78 centièmes

I. L'arrondissement des nombres décimaux

1. L'opération qui consiste à donner la valeur approximative d'un nombre (unité, dixième, centième, etc.) diminue ou augmente le dernier chiffre significatif à toutes les valeurs demandées

1.1 Si le chiffre à la position suivante est 5, 6, 7, 8 ou 9 le chiffre à la position demandée augmente de 1
Ex. : 63,7 = 64
51,46 = 51,5
39,685 = 39,69

1.2 Si le chiffre à la position suivante est 0, 1, 2, 3 ou 4 le chiffre à la position demandée ne change pas
Ex. : 63,4 = 63
51,42 = 51,4
39,684 = 39,68

2. L'arrondissement au dollar est souvent utilisé pour faciliter l'usage des espèces en monnaie et en papier
Ex. : 19,98$ = 20,00$

Chapitre 6 – Le système international

[Voir l'image pleine grandeur]

A. La signification du symbole SI

Le symbole SI signifie Système International d'unités dont les unités courantes sont : la température, la longueur, le volume et la masse

B. La température

C'est le degré Celsius (°C) qui est l'unité de mesure de la température?

• Le thermomètre

1. La température du corps égale 37°C
2. L'eau gèle à 0°C
3. L'eau bout à 100°C
4. La température idéale à l'intérieur est 20°C
5. La forte fièvre est à 40°C
6. La température inférieure à 0°C indique que le mercure descend, alors on utilise le signe -

[Voir l'image pleine grandeur]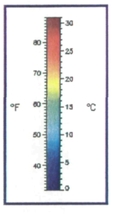

C. La longueur (mètre, centimètre, millimètre, kilomètre, km/h)

1. Le «mètre» est l'unité de base pour les mesures de longueur. Le symbole utilisé est le m (lettre minuscule)

2. Le «centimètre» correspond à la distance entre deux divisions consécutives numérotées sur la règle ou le ruban à mesurer. Le symbole utilisé est cm (lettres minuscules)

[Voir l'image pleine grandeur]

3. Le «millimètre» est la plus petite unité pour la mesure de longueur

3.1 Le symbole utilisé est mm (lettres minuscules)
Le préfixe «milli» signifie «divisé» par 1000 Il y a donc 1000 mm dans 1 m

3.2 C'est la distance entre deux petits traits consécutifs qui se trouvent à l'intérieur d'un centimètre

[Voir l'image pleine grandeur]

4. Le «kilomètre» est la plus grande unité pour la mesure de longueur

4.1. Le symbole utilisé est le km
Le préfixe «kilo» signifie «multiplié par 1000» Il y a donc 1000 m dans 1 km

4.2. La «distance» entre deux villes est mesurée en km
Ex. : Chicoutimi => Québec = 200 km

5. Le «kilomètre/heure» mesure la vitesse

5.1. Le symbole utilisé est km/h (lettres minuscules)
Si un véhicule prend 1 heure pour parcourir 80 kilomètres, on dit que sa vitesse est de 80 km/h

D. Le volume liquide (litre, millilitre)

1. Le litre est l'unité de base pour la mesure du volume «liquide»
Le symbole utilisé est le L ou l
Ex. : un carton de lait

[Voir l'image pleine grandeur]

2. Le millilitre est la plus petite unité pour la mesure du volume «liquide»
Le symbole utilisé est ml (lettres minuscules) Il y a 1000 ml dans 1 litre
Ex. : un médicament

[Voir l'image pleine grandeur]

E. La masse (kilogramme, gramme, milligramme)

1. Le kilogramme est l'unité de base pour la mesure de la masse
Le symbole utilisé est le kg (lettres minuscules)
Ex. : une boîte de sel

[Voir l'image pleine grandeur]

2. Le gramme est une très petite unité de base utilisée dans le SI

• Le symbole utilisé est le g (lettre minuscule)
  - Il y a environ 1000 g dans 1 kg
  - Un crayon pèse environ 1 g

[Voir l'image pleine grandeur]

3. Le milligramme
Le symbole utilisé est le mg (lettres minuscules)

[Voir l'image pleine grandeur]

F. Tableau des symboles des unités de mesure

	Symboles	Unités	Mesures
1. Longueur	km m cm mm	kilomètre mètre centimètre millimètre	1 000 m 1 m 0,01 m 0,001 m
2. Volume liquide	L ou l ml	Litre litre millilitre	1 L 1 l 0,001 l
3. Masse	t kg g mg	lonne kilogramme gramme milligramme	1 000 kg (1 000 000 g) 1 000 g 1 g 0,001 g
4. Aire2	m2 km2	mètre carré kilomètre carré	1 m x 1 m 1 000 m x 1 000 m
5. Volume3	m3 cm3	mètre cube centimètre cube	1 m x 1 m x 1 m 1 cm x 1 cm x 1 cm

[Voir l'image pleine grandeur]

G. Le tableau des équivalences pratiques entre le système métrique et le système impérial

[Voir l'image pleine grandeur]

Chapitre 7 – Le pourcentage

[Voir l'image pleine grandeur]

A. Le symbole (%)

1. Signifie est divisé par «cent»

2. Signifie sur «cent»

3. Se dit et qui se lit «pour cent»

4. Il remplace le dénominateur 100
Ex. : 25 pour cent = 25%
0,25 se lit 25 centièmes

5. Quand on l'écrit, on doit laisser un espace entre le nombre donné et le symbole%
Ex. : 25%

6. De façon courante, un pourcentage ne dépasse pas le cent pour cent
Ex. : 25 pour cent = 25%

7. Utilisé pour : les taxes, les intérêts, les rabais, les résultats et les statistiques

[Voir l'image pleine grandeur]

B. La transformation des pourcentages

• On peut transformer une fraction ordinaire en fraction décimale en divisant le numérateur par le dénominateur

[Voir l'image pleine grandeur]

Remarque : tu conserves deux chiffres après la virgule pour exprimer le pourcentage et il faudra arrondir si le chiffre des millièmes est plus grand ou égal à 5

C. Le vocabulaire lié au pourcentage

Capital	Somme d'argent que l'on peut prêter, placer ou emprunter Un bien
Commission	Pourcentage du montant d'une vente que l'on paie comme salaire à une personne qui vend pour le compte d'une autre personne ou d'une entreprise commerciale
Emprunt	Somme d'argent que tu demandes à une personne ou à une institution bancaire de te prêter pour un certain temps Ex.: Si j'emprunte 100,00$ à un taux d'intérêt de 15%, cela signifie que ma dette sera de 115,00$ après un an
Intérêt	Somme d'argent qui s'ajoute au capital prêté, placé ou emprunté
Rabais	Diminution accordée sur le prix que l'on devrait payer (appelé aussi réduction)
Taux d'intérêt	Pourcentage du capital que l'on ajoutera à une somme prêtée, placée ou empruntée après 1 an Ex.: Si tu places ton argent dans un compte d'épargne à 5% d'intérêt par année, cela signifie que chaque cent dollars (100,00$) te rapportera 5,00$ après 1 an

D. L'équivalence

• Le pourcentage, la fraction décimale et le nombre décimal sont trois façons différentes d'écrire le même nombre
  Ex. : 28% = 28/100 = 0,28

E. Le calcul du pourcentage d'un nombre

• Équivaut à multiplier le pourcentage par ce nombre
  - Il faut transformer le pourcentage en nombre décimal ou en fraction décimale avant d'effectuer la multiplication

[Voir l'image pleine grandeur]

F. La définition de la règle de trois

1. Façon de procéder pour calculer «une valeur inconnue» à partir de «trois données connues» dont deux varient soit directement, soit inversement

G. Les taxes

1. La «TPS»
La taxe sur les produits et services perçue par le gouvernement fédéral

2. La «TVQ»
La taxe sur les produits et services perçue par le gouvernement provincial

[Voir l'image pleine grandeur]

Chapitre 8 – La géométrie

[Voir l'image pleine grandeur]

A. La définition de la géométrie

C'est l'étude des formes (contour d'un objet) ainsi que des dimensions (aire, volume) donc, l'espace occupé par un objet

B. Les instruments de mesure

1. Le compas
Sert à tracer des figures rondes

[Voir l'image pleine grandeur]

2. L'équerre
Sert à construire des angles droits (90°)

[Voir l'image pleine grandeur]

3. Le rapporteur
Propriétés :

• Sert à mesurer ou à construire des angles
• Chaque ligne indique un degré (1°)
• Ce symbole (°) se place en haut et à la droite du nombre (1°)Il contient 180 lignes soit 180°
• Pour la lecture des angles, tu dois placer le centre du rapporteur sur le sommet de l'angle à mesurer
• Pour construire un angle, le centre du rapporteur (à la base horizontale) te sert de point de départ

[Voir l'image pleine grandeur]

Angle droit

[Voir l'image pleine grandeur]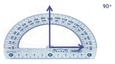

Angle aigu

[Voir l'image pleine grandeur]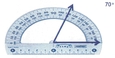

Angle obtus

[Voir l'image pleine grandeur]

C. Le segment de droite

1. La définition
C'est une ligne qui va directement d'un point à l'autre

2. C'est la plus courte distance entre un point de départ et un point d'arrivée

[Voir l'image pleine grandeur]

Remarque : il peut y avoir plusieurs segments sur une droite ou sur une figure

D. Les angles

1. La définition

• C'est l'ouverture entre deux segments ayant le même point de départ
• C'est la figure formée par la rencontre de deux demi-droites

2. La grandeur d'un angle
C'est le petit arc à l'intérieur qui indique l'angle à mesurer

[Voir l'image pleine grandeur]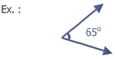

Remarque : dépend toujours de l'ouverture qu'il y a entre les segments et non pas de la longueur de ceux-ci

3. L'appellation dans un angle
Dans un angle, les segments s'appellent «côtés» et le point de départ s'appelle «sommet»

[Voir l'image pleine grandeur]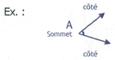

4. L'angle droit
Angle dont la mesure est de 90°

[Voir l'image pleine grandeur]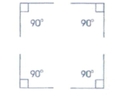

5. L'angle aigu
Angle plus petit qu'un angle droit; sa mesure est inférieure à 90°

[Voir l'image pleine grandeur]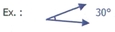

6. L'angle obtus
Angle plus grand qu'un angle droit; sa mesure est supérieure à 90° mais moins de 180°

[Voir l'image pleine grandeur]

7. L'angle plat
Angle dont la mesure est de 180°

[Voir l'image pleine grandeur]

E. Les lignes parallèles et les lignes perpendiculaires

1. Les parallèles
Ce sont des lignes droites qui sont placées à égale distance et qui ne se rencontrent jamais

[Voir l'image pleine grandeur]

2. Les perpendiculaires
Ce sont des segments qui se rencontrent en formant des angles de 90°

[Voir l'image pleine grandeur]

3. La longueur et la largeur
Ce sont les dimensions d'un objet plat parallèle au sol

[Voir l'image pleine grandeur]

Remarque : la longueur est habituellement plus grande que la largeur

4. La base et la hauteur
Ce sont les dimensions d'objets que l'on peut voir de face soit perpendiculaire au sol
Ex. : édifice, maison, etc.

4.1 La base
C'est la dimension d'un côté d'un objet où celui-ci s'élève généralement

[Voir l'image pleine grandeur]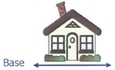

4.2 La hauteur
C'est la dimension de l'élévation d'un objet. La hauteur est une perpendiculaire, donc elle forme un angle de 90° avec la base

[Voir l'image pleine grandeur]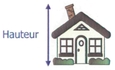

5. Le carré
C'est une figure formée de quatre côtés égaux et de quatre angles de 90°

[Voir l'image pleine grandeur]

6. Le rectangle
C'est une figure formée de deux côtés de longueurs égales, deux côtés de largeurs égales et de quatre angles de 90°

[Voir l'image pleine grandeur]

7. Le triangle rectangle
C'est une figure formée de trois côtés dont un des angles est droit

[Voir l'image pleine grandeur]

F. Le périmètre

1. La définition
C'est la somme des mesures des côtés d'une figure, le tour d'un carré, d'un rectangle, d'un triangle, etc.

2. Les formules :

Carré : côté X 4

[Voir l'image pleine grandeur]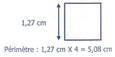

Rectangle : Longueur + largeur X 2

[Voir l'image pleine grandeur]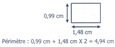

Triangle : côté + côté + côté

[Voir l'image pleine grandeur]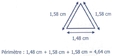

G. L'aire

1. La définition

• C'est la mesure de la surface occupée par une certaine forme géométrique à deux dimensions
  Remarque : la notation finale s'écrit toujours au carré (n²)

2. Les formules :

Carré : côté X côté

[Voir l'image pleine grandeur]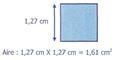

Rectangle : Longueur X largeur

[Voir l'image pleine grandeur]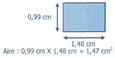

Triangle :

[Voir l'image pleine grandeur]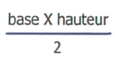

[Voir l'image pleine grandeur]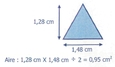

H. Le cercle et le disque

1. La définition

• C'est la ligne courbe que l'on peut tracer à l'aide d'un compas

[Voir l'image pleine grandeur]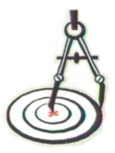

2. Le disque
C'est la mesure de l'aire limitée par le cercle

[Voir l'image pleine grandeur]

3. Le centre
C'est l'endroit où tu places la pointe sèche de ton compas

[Voir l'image pleine grandeur]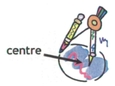

4. Le rayon
C'est tout segment qui relie le point centre à un point du cercle. Il peut y avoir plus d'un rayon

[Voir l'image pleine grandeur]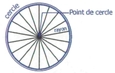

5. Le diamètre

• C'est un segment qui joint 2 points du cercle en passant par le point centre
• Le diamètre est égal à la somme de 2 rayons
• Tous les diamètres d'un même cercle ont la même longueur

[Voir l'image pleine grandeur]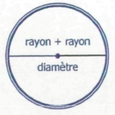

6. La circonférence du cercle

6.1 La définition
C'est la mesure qui fait le contour du cercle

6.2 La formule
Cercle :

[Voir l'image pleine grandeur]

7. L'aire d'un cercle ou d'un disque

7.1 La définition :
C'est la mesure de la surface comprise à l'intérieur de la circonférence d'un cercle

7.2 La formule :
Cercle :

[Voir l'image pleine grandeur]

I. Le volume

1. La définition

• C'est l'espace qu'occupe un objet
  Remarque : la notation finale s'écrit toujours au cube (n3)

2. Les formules :

Figure droite : Longueur X largeur X hauteur

[Voir l'image pleine grandeur]

Cube : Côté X côté X côté

[Voir l'image pleine grandeur]

Chapitre 9 – La calculatrice

[Voir l'image pleine grandeur]

A. La vérification des opérations mathématiques

[Voir l'image pleine grandeur]

Remarque : la majorité des opérations mathématiques peut se vérifier avec la calculatrice

Bibliographie

DFGA et Service d'éducation des adultes, Commission scolaire Thedford-Mines et Black-Lake-Disraëli, 1987, Gouvernement du Québec, ministère de l'Éducation.

BERTHIAUME, Raymond. Mon glossaire mathématique, Québec, Éditions Marie-France ltée, 2000.

Centre Fora, Formation de base, mathématique, Ontario, 2001. Mat-1011-1031.

Adapté de :

DE CHAMPLAIN, Denis, MATHIEU, Pierre, PATENAUDE, Paul, TESSIER, Hélène. Lexique mathématique enseignement secondaire, deuxième édition revue et corrigée, Montréal, Modulo Éditeur, 1996.

MAJEAN, Lucie. L'arithmétique de tous les jours, Pincourt, Eaux Vives.

RENOUVO, Le millepatte sur un nénufar. Édition De Champlain S.F. inc., 2005.

Crédits

Conception
Martine Dompierre et Rémi Gravel

Édition
Isabelle Gaudreault, Christine Tremblay et Sarah Tremblay

Commission scolaire des Rives-du-Saguenay, 2006.

Toute reproduction totale ou partielle, par quelque moyen que ce soit, notamment électronique, mécanique, photocopie, enregistrement, acétate, diapositive, exposé ou autre en tout ou en partie est strictement interdite sans le consentement écrit de la Commission scolaire des Rives-du-Saguenay.

Document produit dans le cadre des Initiatives Fédérales-Provinciales Conjointes en Matière d'Alphabétisation (IFPCA).

Commission scolaire des Rives-du-Saguenay
Service aux entreprises
36, Jacques-Cartier Est
Chicoutimi (Québec)
G7H 1W2

Téléphone : (418) 698-5000, poste 275
Télécopieur : (418)698-5305
Codification: 2006-10-18ct - (487)