Avant-propos

En 1993 paraissait, dans cette même collection, Un visa pour l'alpha pop, la vidéo La sauce à... calculer ou les mathématiques en alphabétisation populaire¹. Cette vidéo, élaborée à partir de quatre sessions de formation², propose une approche de l'enseignement des mathématiques aux adultes analphabètes qui s'éloigne de l'approche traditionnelle du modèle scolaire. Des animatrices et animateurs en alphabétisation populaire ont utilisé cette nouvelle approche et nous livrent, ici, quelques résultats de leurs expérimentations.

Le cahier que vous avez entre les mains veut être un document d'accompagnement à la vidéo. Il contient divers scénarios d'intervention en enseignement des mathématiques. L'approche qui le sous-tend se fonde sur les mêmes principes que ceux avancés dans la vidéo. Parmi ces principes, notons la nécessité de partir des compétences des adultes et celle de recourir à des modèles de référence connus, dont celui de l'argent.

C'est collectivement que les scénarios d'intervention ont été élaborés, expérimentés, puis colligés. Sous la direction de Claude Janvier, didacticien au département d'Informatique et de Mathématiques de l'UQAM, une dizaine d'animatrices et animateurs ont accompli ce colossal travail d'équipe. L'une de ces animatrices, Franchie Loignon, a ensuite procédé à l'organisation et à la rédaction finale des scénarios, en collaboration avec une autre travailleuse de son groupe, Linda Maziade. Le chapitre sur la division, quant à lui, a été conçu et rédigé à partir d'expériences que Françoise Lefebvre a recueillies auprès d'animatrices en alphabétisation populaire.

Les animatrices et animateurs qui ont participé à cette démarche proviennent du Carrefour d'éducation populaire de Pointe St-Charles, du Centre alpha de La Baie, du Centre alpha de St-Honoré, du Centre d'alpha de Prescott, du Centre de lecture et d'écriture, des Centres Mot-à-Mot, du Groupe Atout-Lire et du Groupe Centre-Lac d'Alma. Nous les remercions pour les efforts déployés et la qualité des résultats livrés dans le présent document.

Nous tenons aussi à remercier le professeur Claude Janvier pour la qualité de son travail de supervision. L'Université du Québec à Montréal a généreusement consenti à dégager monsieur Janvier d'une charge régulière d'enseignement afin qu'il puisse offrir la formation sur l'élaboration de scénarios d'intervention d'où origine Mathématiques au quotidien; nous apprécions grandement cette contribution. En dernier lieu, nos remerciements vont à Martine Dompierre, qui, par son document La mise en place d'une cantine étudiante³, a inspiré le chapitre «Un projet de cantine», et à Donald Lurette pour sa contribution au chapitre portant sur la multiplication.

Berthe Lacharité
Service aux collectivités de l'UQAM
et
Regroupement des groupes populaires en alphabétisation du Québec

Introduction

L'introduction des mathématiques dans les ateliers d'alphabétisation populaire pose un double défi aux animatrices et animateurs: d'une part, répondre aux besoins quotidiens des participantes et participants et d'autre part, respecter au jour le jour le mode de fonctionnement des ateliers.

Comme son titre l'indique, Les mathématiques au quotidien se propose de relever ce double défi. Il s'adresse aux animatrices et animateurs des ateliers d'alphabétisation populaire désireux de faire le saut en mathématiques. Complément indispensable à la vidéo La sauce à... calculer ou les mathématiques en alphabétisation populaire, cette nouvelle parution apporte aux animatrices et animateurs un support matériel pour l'encadrement quotidien des activités d'apprentissage en mathématiques.

Redonner confiance

La majorité des participantes et participants des ateliers d'alphabétisation ont développé une crainte, voire une antipathie pour les mathématiques. Rien de surprenant à cela: les mathématiques ont toujours été utilisées comme une matière scolaire servant à sélectionner des candidats et candidates à l'intérieur des écoles.

Plusieurs personnes, en situation d'échec, n'ont jamais pu progresser à l'intérieur du système et ont dû abandonner leurs études. Comme elles se plaisent souvent à dire, «les mathématiques, c'est pour les autres: moi, je n'ai pas l'esprit à cela.»

En général, rien n'indique que l'inaptitude aux mathématiques puisse être innée. Ce qu'il faut plutôt comprendre, c'est que les mathématiques constituent une matière dont la linéarité ne pardonne pas: si, pour une raison quelconque, un élément vient à faire gravement défaut, la suite des événements s'avérera problématique à moins qu'un correctif ne soit rapidement apporté.

Les animatrices et animateurs doivent donc tout d'abord redonner confiance et faire oublier aux participantes et participants des années successives d'échec et de frustration. Cette mise en confiance n'est pas seulement d'ordre affectif; il ne suffit pas de déclarer aux gens qu'ils sont «capables». Il faut prendre les moyens de les faire réussir. L'expérience de la vidéo nous le démontre bien: il faut créer une atmosphère détendue, un climat de confiance et d'harmonie entre les personnes. Cela implique que les animateurs et animatrices elles-mêmes se sentent à l'aise et qu'elles freinent systématiquement les pratiques compétitives qu'on retrouve dans les écoles.

Établir des situations d'entraide dans des groupes hétérogènes

La composition des ateliers d'alphabétisation ayant bien souvent été déterminée à partir des compétences des personnes en lecture et en écriture, le niveau de compréhension et de connaissance des mathématiques variera beaucoup d'une personne à l'autre à l'intérieur d'un même groupe.

Il faut alors chercher à instaurer au sein de l'atelier un climat d'entraide où tout le monde comprend que chacun part de son niveau, que chacun est là pour faire des progrès. Nous avons constaté que cette condition n'est pas facile à réaliser: l'esprit de compétition demeure fortement ancré. C'est en changeant les règles du jeu qu'il est possible de transformer la dynamique du groupe.

Les participantes et participants «forts» sont en général ceux qui calculent vite, mais qui s'avèrent incapables de savoir quoi calculer, leurs capacités reposant trop souvent sur une mémorisation facile à tromper. D'autres, par contre, sans grandes compétences en calcul, peuvent résoudre des problèmes à condition que les nombres soient petits.

En insistant sur les différentes méthodes de calcul, en insistant pour que chaque personne ne donne pas uniquement sa réponse, mais qu'elle explique aussi sa solution, il arrive souvent que le groupe s'étonne de l'ingéniosité des solutions proposées par certaines. C'est à ce moment-là que l'on constate qu'il y a beaucoup de choses à valoriser chez les personnes débutantes et autant de compétences à parfaire chez les plus rapides.

Une méthode intéressante d'encourager la participation de tout le monde consiste à demander à une personne «forte» de poser un problème qu'une «faible» saurait résoudre. En général, les gens qui calculent vite ne peuvent s'imaginer les compétences des autres. Une bonne partie du groupe pourra voir à mieux ajuster la question posée au plus «faible». On peut viser aussi à instaurer une forme de parrainage qui encouragera chaque personne à avoir suffisamment confiance en elle pour travailler à la maison.

Tout ce travail conduit nécessairement à dédramatiser l'erreur chez les personnes participantes, car elles seront plus à même de reconnaître les conditions qui les amènent à errer et deviendront plus attentives à leurs manières de faire. Cette approche visera à faire comprendre au groupe que l'erreur est un instrument de progrès si l'on reste vigilant et que l'on tente d'en tirer leçon. La vidéo La sauce à... calculer comporte une belle scène où l'on voit une participante s'expliquer son erreur et l'attribuer à la complexité des calculs à réaliser au tableau.

L'instauration d'un climat de confiance et d'entraide est un phénomène de groupe: dès que quelques personnes acceptent «d'embarquer», cela provoque une réaction en chaîne; la partie est à moitié gagnée. Il est donc nécessaire de s'assurer la participation de tout le monde.

Partir des compétences des adultes

Tout comme la vidéo, ce document repose sur le principe fondamental qu'il faut partir des compétences des adultes dans l'enseignement des mathématiques en alphabétisation populaire. Ceci signifie que les mathématiques dans les ateliers doivent d'abord se développer au niveau verbal pour progressivement se consolider à l'écrit. En entrant dans les groupes, un grand nombre d'adultes ne savent-ils pas faire fonctionner une arithmétique verbale basée sur le modèle de l'argent: compter par dix, compter par deux, ce qu'il manque à 8,75$ pour faire 10$?

L'utilisation et la manipulation de matériel approprié (argent, blocs de base 10, abaques, réglettes) sont à cette étape d'une grande importance si on veut développer et consolider ces compétences.

On retrouve dans la première partie du document, qui porte sur les opérations de base , un grand nombre d'activités qui montrent précisément comment réaliser le passage du verbal à l'écrit, qui indiquent comment organiser des apprentissages significatifs autour de thèmes intéressants et à partir de matériel structuré dont l'utilisation est bien expliquée.

Rapprocher les mathématiques de la vie de tous les jours

La deuxième partie, «Des projets ou ... les mathématiques au quotidien», propose des projets pouvant être réalisés dans les ateliers et susceptibles d'avoir des retombées dans l'ensemble du groupe. Décrits à partir d'expériences déjà réalisées, ils montrent bien comment rapprocher les mathématiques des préoccupations des participantes et participants et permettent de ne pas isoler les mathématiques du reste de la formation. Par exemple, la préparation d'un spaghetti pour un party de Noël (le projet retenu dans la vidéo) nous a permis, en plus de travailler en groupe sur les opérations mathématiques, d'aborder les factures, les commandes, les unités de mesure (longueur, volume, capacité, masse), le pourcentage, la règle de trois, l'estimation, et elle a fourni un grand nombre d'occasions de lecture et d'écriture.

L'organisation de projets comme ceux présentés dans la deuxième partie du document implique une autre vision de l'apprentissage des mathématiques. En effet, il faudra accepter que le même enseignement puisse conduire à des apprentissages très différents selon les personnes, chacune partant de ses compétences et les développant d'une manière significative.

Dans un contexte où les participantes et participants sont de différents niveaux en mathématiques, il faudra alors orienter le travail en fonction des compétences de chacun. Toutes les participantes et participants n'effectueront que rarement les mêmes tâches. Il ne faut pas penser non plus qu'ils et elles vont toujours appliquer des mathématiques connues: le projet est au contraire une occasion pour apprendre dans un contexte de défi.

Il faut organiser ces projets même si les apprentissages de base ne sont pas encore tous maîtrisés. C'est l'occasion de rassembler toutes les participantes et participants d'un atelier autour d'un projet qui saura les motiver et les faire progresser, quitte à revenir, lorsque le besoin s'en fait sentir, sur les apprentissages de base.

La gestion de tels projets exige par contre plus de dextérité de la part de l'animatrice ou de l'animateur, une plus grande motivation et l'existence dans le groupe de conditions particulières de réalisation. Les projets de cette deuxième partie du document comportent de nombreux sous-thèmes dont on peut s'inspirer pour réaliser des mini-projets de moindre envergure ou des projets similaires adaptés aux besoins des personnes du groupe. Les animateurs et animatrices qui débutent devraient peut-être restreindre dans un premier temps l'ampleur des projets qu'elles seraient tentées de lancer, elles pourraient s'en tenir par exemple à des mini-projets. Sinon, elles risquent fort de se retrouver rapidement dépassées par les événements.

Intégrer les mathématiques dans le quotidien des ateliers

Tout ce plan n'est cependant réalisable que si les participantes et participants «travaillent régulièrement» leurs mathématiques. Une rencontre par semaine ne suffit pas car, comme l'ont constaté plusieurs animatrices et animateurs, on est toujours en train de recommencer. Il faut donc répartir dans la semaine les moments consacrés aux mathématiques. Il faut aussi que s'ajoutent à cela quelques instants de travail à la maison avec le soutien d'une autre personne.

Par contre, il ne faut pas tomber dans le piège inverse et laisser croire que les mathématiques deviennent soudainement faciles. Sans pour autant éliminer une certaine part de mémorisation exigeant un travail soutenu et systématique, il faut cependant recourir à des méthodes qui rassurent les personnes participantes. La mémorisation habituellement ardue peut leur apparaître sous un jour nouveau si l'approche des animatrices et animateurs leur permet de bien comprendre ce qu'elles mémorisent.

Ce document, ainsi que la vidéo, visent donc à renouveler l'apprentissage des mathématiques en alphabétisation populaire. Toute cette entreprise n'est possible que si ceux et celles qui ont contribué à la production du document et de la vidéo ont réussi à vous convaincre de changer votre conception des mathématiques et, surtout, à vous persuader que vous être capables de vous donner les compétences mathématiques et didactiques nécessaires pour favoriser ce renouvellement et y participer.

Claude Janvier

Partie 1 – Activités visant les apprentissages de base

Le dénombrement

[Voir l'image pleine grandeur]

Activité 1 - Mes stratégies pour compter

Objectif de l'activité

Déceler au cours de l'activité le niveau d'habileté de chaque participante et participant sur le plan du comptage.

Difficultés que pose l'activité

Les personnes participantes font naturellement des regroupements lorsqu'elles comptent leur argent. Pourtant, elles ne pensent pas toujours à appliquer ces habiletés quand il s'agit de dénombrer des objets. Les activités suivantes permettront d'une part à l'animatrice ou à l'animateur de voir comment les gens s'y prennent pour compter et, d'autre part, aux participantes et participants de découvrir que leur méthode de calcul de l'argent peut s'appliquer tout aussi bien au calcul des objets. Toutefois, dans cette activité, aucune forme de regroupement n'est suggérée.

Raisonnements impliqués et apprentissages attendus:

• Le regroupement facilite le dénombrement.
• Compter par cinq.

Activité préalable

L'activité s'adresse à tous.

Matériel nécessaire

Une feuille où sont représentés des petits personnages (au nombre de 30).

Fiche 1 – Mes stratégies pour compter

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• montre la fiche 1 et fait estimer le nombre de personnages;
• pose des questions: plus de 100, plus de 10, autour de?, environ combien?;
• distribue la feuille à chaque personne et lui demande de trouver le nombre exact de personnages.

Deuxième étape, travail individuel

Chaque personne calcule sur sa feuille.

Troisième étape

L'animatrice ou l'animateur pose des questions:

• pour amener les participantes et participants à observer la disposition des personnages;
• pour les amener à comparer et discuter les différentes techniques de calcul:

- Qu'est-ce que tu as fait? Pourquoi as-tu choisi cette façon de procéder?
- Combien de personnages dans ce groupe? Peux-tu faire un autre groupe avec autant de personnages?
- Pourrais-tu le faire d'une autre façon?, etc.

Quatrième étape, en groupe

Les participantes et participants comparent leurs façons de procéder:

• Quelle façon semble la plus intéressante? Pourquoi?

Durée de l'activité: une heure

Notes et commentaires

La disposition des personnages où l'on retrouve la configuration du 2, du 3, du 4, du 5 et du 9 est voulue et suggère indirectement un regroupement par 10 et d'autres par 5. Les personnes vont d'abord compter un par un. Il n'y a pas un nombre trop grand de personnages et le calcul leur semble plus simple. Cependant, il faudra suggérer le regroupement si celui-ci n'est pas utilisé.

L'animatrice peut déceler au cours de l'activité le degré de connaissances de chacune des personnes du groupe.

Pour ceux et celles qui éprouvent des difficultés, on pratiquera le calcul par 5 soit avec le tableau suivant, soit avec des 5¢ ou des 5$, soit avec les 5 minutes inscrits sur une horloge, parce que ce sont des éléments familiers.

Oralement, on initiera à la multiplication et à la division par 5 à l'aide de questions: combien font trois groupes de cinq, quatre groupes de cinq et, inversement, combien de groupes de cinq peux-tu faire avec 20, 25, 30 personnages?

Les personnes les plus avancées feront les combinaisons d'addition sur des cartons pour les moins avancées: 9 et 2, 9 et 3, 9 et 4, 9 et 5, 9 et 6, etc.

Le tableau qui suit deviendra l'outil pour apprendre à compter par 5 et par 10.

Consignes pour compléter la fiche 2:

Compter les carrés de gauche à droite. Avec un marqueur ou un crayon de couleur pâle, colorier le cinquième carreau. Poursuivre le calcul de 1 à 5 et colorier le nouveau carreau. Nous aurons la cinquième et la dixième colonne en couleur.

Puis on complète le tableau en inscrivant les chiffres de 1 à 100. Les multiples de 5 seront tous coloriés. On utilisera le même tableau pour pratiquer les multiples de 2, 3, etc.

[Voir l'image pleine grandeur]

Fiche 2 – Compter par...

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Activité 2 - Montre-moi comment tu comptes

Objectif de l'activité

Déceler au cours de l'activité le degré d'habileté de chaque participante et participant en ce qui concerne le comptage.

Difficultés que pose l'activité

Le calcul à l'unité est facile lorsque la quantité est restreinte. Mais lorsque le nombre augmente, les personnes participantes ont de la difficulté à retenir où elles en sont dans leur calcul. La difficulté à nommer et à retenir le nombre amène souvent des erreurs et oblige parfois à tout recommencer. C'est à ce moment-là que le regroupement devient utile et nécessaire.

Raisonnements impliqués et apprentissages attendus:

• Le regroupement facilite le dénombrement
• Apprendre à compter sans se tromper malgré les contraintes.
• Faciliter le passage aux dizaines suivantes (ex. 49-50, 59-60).
• Compter par 50 et par 20.

Activités préalables

• Avoir fait la première activité.
• Savoir compter au-delà de 100.
• Savoir associer l'ensemble au nombre d'éléments qu'il contient.

Matériel nécessaire

Objets divers en grande quantité
(jetons de bingo, bâtonnets de café, sous noirs ou blocs base dix)

Déroulement: les étapes

Première étape, travail en équipes de deux ou trois personnes

L'animatrice ou l'animateur:

• distribue les objets à chaque équipe (plus de 100);
• montre un groupe d'objets et fait estimer le nombre;
• pose des questions: plus de 100, plus de 200, autour de, environ combien?
• demande aux gens de trouver le nombre exact.

Deuxième étape

Chaque groupe calcule selon sa méthode.

L'animatrice ou l'animateur circule d'un groupe à l'autre et observe les techniques de chacun.

Troisième étape

L'animatrice ou l'animateur questionne chaque groupe pour amener les gens à discuter de leurs techniques de calcul:

• Qu'est-ce que vous avez fait? Pourquoi avez-vous choisi cette façon de faire?
• Êtes-vous sûrs de votre nombre?
• Comment pouvez-vous m'assurer qu'il y a bien le nombre indiqué et qu'il n'y a pas d'erreur?
• Pouvez-vous trouver une autre façon de calculer?

Quatrième étape

Susciter les comparaisons et la discussion sur les différents regroupements effectués.

• Est-ce la même chose que compter de l'argent?
• Quelle façon de faire semble la plus intéressante? Pourquoi?, etc.

Les scénarios: exemple des regroupements réalisés

Équipe 1:

50 - 50 - 50 - 20 - 20 - 20 - 20 -20 - 20 - 20 - 20 - 20 - 20 - 1 – 1

devient après discussion:

(50 - 50) (20 - 20 - 20 - 20 - 20) (20 - 20 - 20 - 20 - 20) (50) (1-1)

Les gens éprouvent de grandes difficultés à compter à partir d'une dizaine impaire 150 + 20 + 20 + 20... ce qui explique le regroupement retenu.

Équipe 2:

60 - 60 - 50 - 50 - 25 - 10 - 10 -10 -13

devient après discussion:

(60 - 60) - (50 - 50) - 20 - 10 - 10 - 10 - 10 - 3 - 5

La diversité des regroupements rend le calcul difficile et long. Il faut donc uniformiser les regroupements.

Équipe 3:

100 - 100 - 30 - 36

devient après discussion:

100 - 100 - 30 - 30 - 6

Le regroupement par 30 et par 60 n'aurait jamais été utilisé dans le calcul de l'argent. Pourtant, avec des objets, les gens vont y recourir alors qu'aucune raison particulière ne le justifie. Nous le considérons comme un regroupement moins coutumier que les autres.

Durée de l'activité: deux heures

Notes et commentaires

Les personnes participantes doivent comprendre, à ce stade, à quel point le regroupement est utile pour dénombrer un grand nombre d'objets. De plus, elles peuvent constater que certains regroupements sont plus faciles que d'autres et que plus les regroupements sont différents, plus le calcul est complexe (ex. Groupe 2).

C'est aussi à ce stade que se fait la comparaison avec l'argent et que la généralisation peut s'appliquer. Plusieurs personnes, inspirées par le calcul de l'argent, auront réalisé les regroupements suivants:

• Le calcul par 50 (deux groupes de 50 font 100; trois font 150).
• Le calcul par 20 (cinq groupes de 20 font 100; dix font 200).
• Le calcul par 10 (cinq groupes de 10 font 50; dix font 100).

Enrichissement:

Travailler avec les objets de chaque équipe.

On demande, par exemple, aux personnes des équipes 2 et 3 de refaire les calculs de l'équipe 1. On vérifie le degré de connaissances à l'aide de ces questions:

• Combien peut-on faire de groupes de 20 avec les deux groupes de 50?
• Combien de groupes de 10 peut-on faire avec les cinq groupes de 20?
• Combien de groupes de 20 peut-on faire avec le groupe de 60?
• Combien de groupes de 10 avec le même groupe de 60?
• Combien d'objets dans les quatre groupes de 10?
• Combien de groupes de 50 peut-on faire avec le groupe de 60 et que reste-t-il?
• Combien de groupes de 50 peut-on faire avec les deux groupes de 100?
• Combien de groupes de 20 peut-on faire avec les deux groupes de 30?
• Avec un groupe de 30? Que reste-t-il?

Imprimer l'exercice complet

Activité 3 - Des stratégies pour mieux compter

Objectif de l'activité

Amener les participantes et participants à développer des techniques particulières de dénombrement et de regroupement

Difficultés que pose l'activité

On retrouve dans les activités qui suivent les mêmes contraintes que dans les précédentes. Ces dernières n'étaient toutefois pas dirigées, alors que maintenant, les exercices comportent une disposition semi-organisée (groupes de deux) ou suggèrent une forme de regroupement.

Raisonnements impliqués et apprentissages attendus:

• Certains regroupements sont plus faciles que d'autres.
• Compter par 2.

Activités préalables

Avoir suivi les activités 1 et 2.

Matériel nécessaire

Fiche où sont représentés un certain nombre de crayons.

Fiche 3 – Mes stratégies pour compter

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• montre la fiche 3 et fait estimer le nombre de crayons;
• pose des questions: moins de 100, plus de 10, autour de, environ combien?;
• distribue la fiche à chaque personne et lui demande de trouver le nombre exact de crayons.

Deuxième étape, travail individuel

Chaque personne calcule sur sa feuille.

Troisième étape

L'animatrice ou l'animateur:

• pose des questions afin de comparer et de discuter les différentes techniques de calcul de chaque personne:

- Qu'est-ce que tu as fait?
- Pourquoi as-tu choisi cette façon de faire?
- Pourrais-tu le faire d'une autre façon?

Quatrième étape

Les gens comparent les différents regroupements à partir de leur feuille: quelle façon de procéder semble la plus intéressante? Pourquoi?

Les scénarios: exemples des regroupements réalisés

On a compté un par un.
Les personnes qui comptent les objets un par un n'ont pas encore saisi F avantage du regroupement. Elles éprouvent des difficultés avec la récitation des nombres et avec le passage aux dizaines suivantes.

On a regroupé par deux, en encerclant chaque groupe de deux objets.
On compte par deux jusqu'à 12 pour ensuite continuer un par un, 13-14, 15-16, 17-18, en mettant l'accent sur le multiple de 2.

On a regroupé par lignes pour ensuite additionner les nombres obtenus.
Les regroupements ainsi effectués sont aussi nombreux que le nombre de lignes. Le dénombrement est plus difficile et exige un calcul par écrit.

Durée de l'activité: une heure

Notes et commentaires

La disposition suggère le regroupement par deux. Il serait facile de passer ensuite au regroupement par 10. Pourtant, personne n'a pensé à utiliser ce cheminement. Il serait préférable de présenter l'exercice avec une deuxième disposition, comme celle figurant à la fiche 4, afin de susciter sans le demander ou le dire le regroupement par deux puis par 10. Ensuite en comparant les deux feuilles, on fera ressortir l'avantage du regroupement par 10.

Fiche 4 – Mes stratégies pour compter

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Activité 4 - Regrouper pour mieux compter

Objectif de l'activité

Amener les participantes et participants à développer des techniques particulières de dénombrement et de regroupement.

Difficultés que pose l'activité

On retrouve dans les activités qui suivent les mêmes contraintes que dans les précédentes. Ces dernières n'étaient toutefois pas dirigées, alors que maintenant, les exercices comportent une disposition semi-organisée qui suggère une forme de regroupement (les verres).

Raisonnements impliqués et apprentissages attendus:

• Les regroupements par un, par 10 et par 100 sont la base du système d'écriture et de lecture des nombres.
• Ces regroupements portent les noms d'unité, de dizaine et de centaine.

Activités préalables

• Savoir compter au-delà de 100.
• Savoir associer l'ensemble au nombre d'éléments qu'il contient.
• Avoir suivi les activités précédentes.

Matériel nécessaire

• Des sous noirs ou jetons de bingo en grande quantité
• Des verres en plastique (genre verres à bière) d'au moins deux tailles différentes

Déroulement: les étapes

Première étape, en équipes de deux ou trois personnes

L'animatrice ou l'animateur rappelle les constatations précédentes:

• le regroupement facilite le dénombrement;
• il est plus facile de compter des regroupements semblables;

L'animatrice ou l'animateur:

• distribue à chaque équipe des jetons ou des sous noirs (plusieurs centaines);
• distribue des petits verres et des grands verres;
• donne la consigne de compter les sous et de les «regrouper» dans les verres en utilisant des regroupements faciles.

Deuxième étape

Chaque groupe dénombre selon sa méthode. L'animatrice ou l'animateur:

• circule d'un groupe à l'autre et observe les techniques de chacun;
• dirige l'exercice afin d'amener les participantes et participants à rassembler les sous ou les jetons par groupes de 100 et de 10, et à les placer dans les verres.

Questions pour orienter le regroupement:

• Comment pouvez-vous m'assurer que vous avez trouvé le bon nombre et qu'il n'y a pas d'erreur?
• Quel regroupement pouvez-vous utiliser?
• Y a-t-il des regroupements plus faciles que d'autres? Pourquoi?

Troisième étape, en grand groupe

Découvrir des liens.

On représente par un dessin au tableau les verres utilisés: on peut voir deux grands verres, six petits verres et trois sous noirs pour 263 sous.

[Voir l'image pleine grandeur]

En mathématiques, on donne un nom à chacun de ces regroupements: ce sont l'unité, la dizaine et la centaine.

(Faire ressortir le lien entre un et unité, dix et dizaine, cent et centaine)

Notes et commentaires

Le regroupement par 10 est le principe de base de l'écriture des nombres et de toutes les opérations subséquentes. Dans les activités précédentes, les regroupements ont été davantage réalisés à partir du modèle de l'argent et variaient d'un groupe à l'autre. Il faut maintenant apprendre à utiliser ce modèle à base 10 pour établir et consolider les fondements et les principes mathématiques.

Lors de l'expérimentation pratique, l'une des équipes ne s'était donné aucune directive de départ. Chaque personne du groupe a compté puis placé sa poignée de sous dans des verres sans considérer la quantité et la dimension du verre. Il était impossible de dire à la fin combien de sous contenait un verre, grand ou petit Il fallait estimer au poids pour savoir s'il contenait 50, 75 ou 100 pièces. Avec l'aide de l'animatrice, le groupe a alors adopté une démarche différente en convenant de mettre 100 sous dans les grands verres, 10 sous dans les petits verres et le reste à côté.

Il faut amener les gens à découvrir le lien entre les verres utilisés pour dénombrer les sous et la valeur positionnelle des chiffres dans le nombre.

Certaines personnes ont de la difficulté à lire les nombres supérieurs à 100. Il faut faire la lecture du nombre à partir des verres: ainsi, deux grands verres font deux cents, puis compter par 10 les six petits verres pour obtenir 60 et les unités pour obtenir 3.

Enrichissement:

Illustrer avec les verres (ou autres objets) les nombres 358, 149, 205, 300. À ce moment-là, il n'est plus nécessaire de mettre des sous dans les verres.

On reproduit le dessin au tableau, on indique les chiffres sous les dessins, puis on lit le nombre obtenu.

Il faut répéter l'exercice plusieurs fois et utiliser les verres pour expliquer le rôle du zéro dans les nombres.

Exemple:

L'animatrice ou l'animateur place trois grands verres et cinq sous sur la table (305). Elle ou il demande combien cela représente de sous.

• Comment lire ce nombre?
• Comment écrire ce nombre au tableau?
• Est-ce que 35 représente bien le nombre?
• Qu'est-ce qui manque?
• Que faut-il mettre à la place du petit verre?

Le zéro est utilisé pour indiquer qu'il n'y a rien à la place des sous ou des petits verres.

Imprimer l'exercice complet

Activité 5 - Des stratégies pour compter plus vite

Objectif de l'activité

Permettre aux participantes et participants d'approfondir les techniques de dénombrement et de regroupement.

Les exercices 5 et 6 de dénombrement proposent une disposition déjà organisée (groupes de 10 ou regroupements d'objets par 10 et par 100).

Difficultés que pose l'activité

Compter sans se tromper malgré les contraintes.

Raisonnements impliqués et apprentissages attendus:

• Les regroupements par 10 et par 100 facilitent le dénombrement
• Le calcul par 10.

Activités préalables

• Savoir compter au-delà de 100.
• Savoir associer l'ensemble au nombre d'éléments qu'il contient.

Matériel nécessaire

Fiche illustrant un certain nombre de personnages (plus de cent).

Fiche 5 – Trouve une façon rapide de compter les petits bonshommes

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• présente la fiche 5 et fait estimer le nombre de personnages;
• pose des questions: plus de 20, moins de 100, autour de, environ combien?;
• distribue la fiche à chaque personne et lui demande de trouver le nombre exact de personnages.

Deuxième étape

Chaque personne dénombre sur sa fiche.

Troisième étape

L'animatrice ou l'animateur:

• dirige l'exercice afin d'amener les participantes et participants à rassembler les personnages par groupes de 10 (une colonne);
• amène les personnes à découvrir des liens:

- Peut-on faire des liens entre les verres et les petits bonshommes?
- Y a-t-il quelque chose de pareil?
- Comment appelle-t-on: un groupe de cent? un groupe de dix? les objets non regroupés?
- On écrit le nombre au tableau.
- Quel lien remarquez-vous entre les groupes et le nombre inscrit? 146 c'est:1 groupe de 100; 4 groupes de 10; 6 bonshommes seuls.

Notes et commentaires

Par cet exercice, l'animatrice ou l'animateur vérifie si la notion du regroupement par 10 est bien comprise.

Les gens peuvent compter par 10 jusqu'à cent, ou encore compter 10 colonnes pour avoir un groupe de 100.

Cet exercice peut aussi être mis en lien avec les blocs base-dix.

On retrouvera des exemples dans la vidéo La sauce à... calculer.

Imprimer l'exercice complet

Activité 6 - Le regroupement par 10 et 100 [...]

Le regroupement par 10 et 100 facilite le dénombrement

Objectifs de l'activité

Permettre aux participantes et participants d'approfondir leur compréhension de la numération à base 10.

Faire découvrir et reconnaître la position de l'unité, de la dizaine et de la centaine.

Difficultés que pose l'activité

Les gens savent classer des objets. Les exemples ne manquent pas et sont faciles à trouver dans la vie de tous les jours (ustensiles de cuisine, lingerie, outils ou billets de banque). Il faut donc partir de ces connaissances pour introduire les notions de centaines, dizaines et unités qui sont des classes ou regroupements de nombres. L'étude de ces principes de numération aidera à mieux comprendre les techniques algorithmiques, de même que certaines propriétés des opérations où ils sont couramment appliqués.

Raisonnements impliqués et apprentissages attendus:

• Comme les objets, les nombres se classent par groupe.
• La position de chaque chiffre dans un nombre indique à quel groupe il appartient et détermine sa valeur.

Activités préalables

Exercices de classification.

Matériel nécessaire

• Différents objets (trois sortes au moins) à l'unité, en paquets de 10 et en paquets de 100
• Un carton de 20 par 60 cm

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• place tous les objets pêle-mêle sur la table et demande aux gens de les classer,
• les jetons à l'unité et les verres contenant des jetons vont ensemble;
• les bâtons à l'unité et les bâtons attachés en paquets de 10 et de 100, vont ensemble;
• les anneaux à l'unité et les anneaux passés dans une corde en paquets de 10 et de 100 vont ensemble.

Deuxième étape

L'animatrice ou l'animateur:

• demande ensuite aux participantes et participants de classer et de placer les jetons sur le carton selon les regroupements;
• leur demande de nommer chaque catégorie: unités, dizaines, centaines.

Les jetons seuls sont les unités; les jetons dans les petits verres sont les dizaines; les jetons dans les grands verres sont les centaines.

Troisième étape

L'animatrice ou l'animateur:

• introduit la représentation symbolique et fait le portrait du nombre au tableau:

[Voir l'image pleine grandeur]

• Que représente le grand carré?
• Que représentent les petits carrés?
• Que représentent les barres?
• Comment lire ce nombre?

Quatrième étape

Faire des exercices semblables.

Représenter et lire le nombre qui a 4 centaines, 3 dizaines et 5 unités avec des symboles.

Trouver le nombre représenté par:

[Voir l'image pleine grandeur]

Cinquième étape

Placer les chiffres dans une grille semblable au tableau, puis sur une feuille.

[Voir l'image pleine grandeur]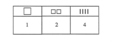

Reprendre les étapes 2 et 3 avec les autres objets.

Durée de l'activité: deux heures

Imprimer l'exercice complet

Commentaires généraux sur le dénombrement

Nous avons expérimenté ces exercices avec des personnes qui débutaient en calcul. Cependant, il serait pertinent et même important de présenter ces activités aux personnes plus avancées. Car lorsqu'on examine attentivement les difficultés rencontrées par ces dernières, on établit vite le lien entre ces difficultés et la mauvaise connaissance du système de numération à base dix. En fait, certaines personnes qui participent aux ateliers de calcul ne saisissent pas le concept du nombre. C'est-à-dire qu'elles savent en général réciter sans trop se tromper la suite des nombres, mais cette activité est parfois mécanique. De plus, plusieurs personnes se heurtent aussi au problème de l'écriture et de la lecture des nombres, à cause d'une méconnaissance de la valeur positionnelle de ceux-ci. Enfin, les principes de la numération et les relations à établir entre ce système et les algorithmes¹ n'apparaissent pas du tout clairs et sont à la source de ces difficultés.

Il serait bon de suivre l'ordre et les étapes des activités proposées ici. Les activités 1, 3, et 5 sont plutôt des activités diagnostiques ou d'évaluation et ne devraient pas être écartées.

La dernière étape incluant la grille est importante. Elle précise et favorise l'écriture et la lecture des nombres, détermine la position et la valeur des chiffres et prépare les participantes et participants à comprendre la technique de l'addition et de la soustraction. Elle leur permet aussi de mieux comprendre le rôle du zéro.

1. Algorithme: processus de calcul ou ensemble des règles de calcul permettant d'arriver à un résultat final déterminé. On dit aussi opération mathématique.

L'addition

[Voir l'image pleine grandeur]

Activité 1 - Des verres et des grilles [...]

Des verres et des grilles pour découvrir les règles de l'addition sans retenue

Objectifs de l'activité

Permettre aux participantes et participants de préciser le sens de l'addition.
Faire découvrir ses règles mathématiques.

Difficultés que pose l'activité

Les personnes que nous retrouvons dans les ateliers de calcul connaissent généralement la notion, le sens de l'addition en termes de réunion, d'ajout, de «plus» sans nécessairement nommer l'opération comme telle. Elles savent par exemple que la taxe s'ajoute au prix d'achat, que le coût de l'électricité augmente le coût du loyer, qu'en mettant des choses ensemble, il y en a plus. Par conséquent, les activités subséquentes permettent, d'une part, de préciser le sens de cette opération, de lui donner un nom et, d'autre part, de saisir les principes et les règles de l'addition. Nous tenterons aussi d'appliquer les apprentissages précédents à ces nouvelles situations pour ainsi découvrir les techniques de l'addition.

Raisonnements impliqués et apprentissages attendus:

Comme les objets, les nombres se classent par groupes: les unités s'ajoutent aux unités, les dizaines aux dizaines et les centaines aux centaines.

Activités préalables

Avoir précisé le sens de l'addition en demandant aux participantes et participants d'en donner des exemples tirés de leur quotidien.

Matériel nécessaire

• Des objets à l'unité et regroupés en paquets de 100 et de 10
• Des cartons rectangulaires d'environ 60 par 20 cm

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• travaille avec les objets devant les participantes et participants;
• utilise des situations concrètes d'addition en ajoutant des paquets ou des unités et fait le raisonnement à haute voix.

Il faut veiller à présenter l'addition non seulement sous forme de réunion mais aussi d'ajout: combien dois-je ajouter de verres pour avoir..., qu'est-ce que j'obtiendrai si j'en mets six de plus?

Exemple:

J'ai un grand verre de 100 jetons, trois petits verres de dix jetons et deux jetons seuls.
Mon voisin me donne six jetons et deux petits verres de dix jetons chacun.

L'animatrice ou l'animateur:

• fait le raisonnement: les nombres se classent par groupes comme les objets; donc, je mets les grands verres ensemble, les petits verres ensemble et les jetons à l'unité ensemble.

[Voir l'image pleine grandeur]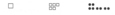

J'ai maintenant un grand verre, cinq petits verres et huit jetons.

Pour aider les participantes et participants à bien positionner les groupes, on peut placer les objets sur un carton rectangulaire d'environ 60 par 20 cm, divisé en trois sections. Au bas de chaque carré sont inscrits les mots et les chiffres: centaine 100, dizaine 10, unité 1.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur:

• demande aux participantes et participants de faire la même chose sur leur carton en utilisant des objets et d'autres nombres.

Lorsque les gens se seront familiarisés avec les outils (carton et objets), on travaillera sur des problèmes tirés du quotidien à l'aide de ce matériel. Ce dernier permet d'utiliser des nombres plus grands et plus proches de la réalité des participantes et participants. On s'en tiendra d'abord aux additions sans retenue. Cependant, on peut faire des additions de deux, de trois et même de quatre chiffres.

L'animatrice ou l'animateur pose des questions:

• Où placez-vous vos jetons?
• Pourrait-on mettre les jetons à l'unité dans un petit verre
• Pourquoi?

Deuxième étape

Les participantes et participants travaillent avec des dessins seulement, au tableau ou sur une feuille. Ils ou elles trouvent des situations d'addition.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur pose des questions:

• Combien as-tu de verres maintenant?
• Quelle opération as-tu fait?

En calcul, lorsqu'on met des choses ensemble ou qu'on ajoute une quantité à une autre quantité, on donne un nom à cette action ou opération: c'est une addition. On dit qu'il faut additionner. On peut dire aussi faire un plus. C'est le signe + qui indique l'addition.

Troisième étape, passage à l'écriture algorithmique

L'animatrice ou l'animateur:

• propose un problème d'addition;
• place ensuite les dessins et les chiffres dans les grilles, comme ci-dessous;
• explique chaque façon de représenter l'addition. Chaque grille, bien que différente, représente la même chose.

[Voir l'image pleine grandeur]

Quatrième étape

On demande ensuite à une personne du groupe de refaire la même chose au tableau en choisissant l'une des quatre manières présentées pour illustrer un autre problème. Puis, une autre personne doit aller au tableau à son tour en utilisant une autre façon de faire et ainsi de suite. On compare ensuite les réponses pour se rendre compte que le résultat est toujours le même.

On peut expliquer le zéro dans l'addition à l'aide des grilles et des verres. Certaines personnes éprouvent des difficultés sur ce plan. Il s'agit de leur faire comprendre que le zéro indique l'absence d'un groupe et n'annule pas le reste de l'addition (six plus zéro donne six, et non zéro).

Durée de l'activité: deux heures

Imprimer l'exercice complet

Notes et commentaires

En travaillant avec les objets et les grilles, les participantes et participants font naturellement l'addition en commençant par les centaines. Cette façon de procéder permet d'abord une meilleure estimation du résultat et favorise ainsi le calcul mental. A cette étape, cette approche ne pose pas de difficultés puisqu'il n'y a pas de retenue. Il est bon, cependant, de leur faire remarquer que l'on obtient le même résultat en commençant par les unités.

La représentation des nombres sous différentes formes et l'utilisation des grilles aident les participantes et participants à mieux intégrer les règles de la numération et des regroupements. En plus de jouer le rôle d'agents renforçateurs, ces exercices laissent aux personnes la possibilité de choisir la méthode qui leur convient. Les personnes moins avancées utilisent les dessins alors que les plus avancées passent directement à l'écriture algorithmique.

Activité 2 - La manipulation dans l'apprentissage de la retenue

Objectifs de l'activité

Permettre aux participantes et participants de préciser le sens de l'addition.
Faire découvrir les règles mathématiques de la retenue.

Difficultés que pose l'activité

C'est à cette étape que les notions de regroupement et de valeur positionnelle interviennent; il est important de maîtriser ces notions pour effectuer correctement les opérations arithmétiques de base. En effet, la retenue mais aussi l'emprunt découlent de ces connaissances. Les exercices sur le dénombrement avaient pour objectif d'introduire les principes du système de numération. Il faut maintenant amener les gens à appliquer ces mêmes principes à l'algorithme de l'addition.

Cependant, cette perception des choses n'est pas toujours évidente. Par exemple, certains vont aligner 12 unités plutôt que d'utiliser le regroupement du 10 et du 2. Il faut faire en sorte que les gens aient conscience que 10, c'est aussi 1 du groupe suivant (la dizaine), que 12 c'est 10 et 2, et-ainsi de suite.

Raisonnements impliqués et apprentissages attendus:

• Reconnaître la valeur positionnelle des chiffres.
• Comprendre le sens de la retenue.

Activités préalables

• Travailler sur la perception du 10 dans les nombres de 11 à 19.
  Par exemple, travailler avec des sous noirs et des dix sous ou faire des emballages et des regroupements de 10.
• On travaillera aussi l'addition de petits nombres en utilisant des barres et des carrés:

[Voir l'image pleine grandeur]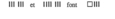

Matériel nécessaire

Trois sacs de jetons

Déroulement: les étapes

Première étape

L'animatrice ou l'animateur:

• présente le problème d'addition: j'ai trois sacs de jetons;l'un contient 224 jetons, l'autre 43 jetons et le troisième 146 jetons. Je mets tous les jetons dans un grand sac.

- Combien y a-t-il de jetons dans le grand sac?
- Quelle opération faut-il faire?

• explique et exécute la démarche elle-même, d'abord avec les verres:

[Voir l'image pleine grandeur]

Dans mon premier sac, j'ai 224 jetons: c'est deux verres de 100, deux verres de 10 et quatre jetons, et ainsi de suite.

• demande aux participantes et participants comment regrouper autrement les jetons pour avoir le total;
• reprend plusieurs exercices semblables.

Deuxième étape

L'animatrice ou l'animateur:

• dessine la grille au tableau pour inscrire les chiffres;
• inscrit les chiffres dans la grille;
• calcule chaque colonne et regroupe «en paquets» de 10;
• écrit la réponse sous la colonne;
• transporte «le groupe de 10» dans la colonne de gauche;
• complète et explique la démarche.

[Voir l'image pleine grandeur]

Troisième étape

Les participantes et participants refont la même chose avec d'autres nombres en utilisant le même procédé que dans l'activité 1 avec les quatre types de présentation.

Durée de l'activité: deux heures et plus

Commentaires généraux sur l'addition

Le travail avec les grilles et les verres illustre bien le rôle de la retenue et permet de démontrer l'importance de bien positionner chacun des chiffres. Certaines personnes ont tendance à aligner tous les chiffres à partir de la gauche, ce qui donne l'erreur suivante:

[Voir l'image pleine grandeur]

C'est aussi l'occasion d'expliquer l'avantage de la technique de l'addition écrite. Par exemple, en commençant l'addition par les unités, on élimine les occasions de se tromper et on obtient le même résultat. Il sera donc souvent utile de revenir aux verres pour mieux faire comprendre pourquoi il faut placer les chiffres à partir de la droite.

Au cours de cette démarche, il ne s'agit pas d'imposer le calcul avec les quatre grilles. Certaines personnes trouvent difficile de compléter toutes les grilles. Elles préfèrent une méthode en particulier et c'est avec cette méthode qu'il faut travailler.

Au moment de l'expérimentation, nous avons travaillé avec différents objets: sous noirs, bâtonnets de café, jetons de bingo, gobelets à médicament, verres en plastique. Il reste évident que le modèle de l'argent demeure le plus proche des gens et sert facilement de point de comparaison. Mais il reste qu'il est important d'utiliser des objets divers pour l'apprentissage du dénombrement, de l'addition et des autres opérations qui suivront, parce que cela permet la généralisation.

Nous avons pu constater à l'expérimentation que les verres en plastique s'avèrent les plus intéressants et que, de plus, ils ne coûtent presque rien. (L'emprunt se démontre facilement avec dix petits verres empilés dans le grand verre de la centaine, par exemple).

Le carton divisé en trois constitue aussi un outil pratique et pertinent. Et lorsque les personnes ont bien saisi le concept de la centaine, de la dizaine et de l'unité, on utilise seulement des jetons de couleurs différentes pour illustrer le nombre, ceci avant de passer à l'opération écrite.

Il faut bien sûr intégrer ces apprentissages à l'intérieur d'une situation concrète (par exemple, le calcul des dépenses fixes de son budget, la cantine, les semis), où il faudra d'abord saisir le sens de l'opération et découvrir où se situent les difficultés rencontrées par chaque individu.

Imprimer l'exercice complet

La soustraction

[Voir l'image pleine grandeur]

Activité 1 - Les sens cachés de la soustraction

Objectifs de l'activité

Permettre aux participantes et participants de préciser le sens de la soustraction.
Faire découvrir les techniques de la soustraction simple.

Difficultés que pose l'activité

Techniquement, l'apprentissage de l'addition et de la soustraction devrait se faire en même temps, la soustraction étant «l'inverse» de l'addition.

Les gens reconnaissent l'opération 5 + 4 = 9; ils sont en mesure de dire que si on enlève 5, il reste 4. C'est une opération mathématique facile à comprendre et à résoudre. Cependant, si cela se perçoit facilement avec de petits nombres, il devient plus difficile de saisir et de vérifier à mesure que les quantités augmentent.

Les personnes qui participent aux ateliers de calcul ne connaissent pas toujours le sens de la soustraction. Mais dans la réalité, les gens savent que si on enlève une certaine quantité, si on dépense son argent, il en reste moins. C'est le sens premier de la soustraction.

Ils comprennent aussi que si quelque chose coûte 45$ et qu'ils n'ont que 29$, il leur manque de l'argent Nous avons ici un deuxième sens à la soustraction qui est, en fait, une addition de complément.

Ils savent encore qu'un article à 18$ est moins cher qu'un article à 31$. Nous retrouvons ici un troisième sens à la soustraction, à savoir un sens de comparaison.

Ce sont trois situations qui demandent une soustraction pour arriver à la solution. Certaines personnes ayant des difficultés d'abstraction seront incapables de dire quelle opération il faut faire pour résoudre les deux derniers problèmes. Il est facile de comprendre la confusion que créent de telles situations lorsqu'on travaille avec des nombres sans support visuel ou si on demande d'effectuer l'opération mathématique. Conséquemment, dans l'opération mathématique, il faut viser à ce qu'on puisse faire abstraction de la situation physique pour travailler sur des nombres seulement.

Prenons l'exemple suivant. Pour la cantine, on a acheté 54 jus et il en reste 28.
Combien de jus a-t-on vendus? Ce problème, qui paraît simple en soi, comporte plusieurs
difficultés. D'abord le sens, qui demande de compléter pour savoir ce qui manque pour
se rendre à 54. Le problème se pose ainsi pour la majorité des adultes: 28 + = 54.

Cela implique que les gens aient une bonne notion des nombres ou qu'ils saisissent bien le concept de l'addition et de la soustraction de manière à pouvoir déduire qu'en soustrayant, on trouvera le terme manquant. Deuxièmement, l'opération mathématique comporte un emprunt. On doit donc faire abstraction de la situation réelle (on achète les jus en paquets de 3 ou en caisses de 24) pour dire, au moment de l'opération 54 - 28: «Il faut que j'emprunte une dizaine ou un paquet de dix», ce qui, dans les faits, ne correspond nullement à la réalité.

Le concept de la soustraction est difficile à comprendre et à enseigner, d'autant plus que plusieurs personnes ne connaissent pas suffisamment les combinaisons de base. En conséquence, il faut favoriser la mémorisation de ces calculs en prolongeant les activités antérieures de manipulation.

Ainsi, les activités proposées permettent d'une part, de préciser les sens de la soustraction, de distinguer les situations qui font référence à l'un ou à l'autre des sens, de savoir quand la soustraction est utile pour résoudre un problème et, d'autre part, d'en saisir les principes et les règles. De plus, nous tenterons de transposer les apprentissages précédents à ces nouvelles situations pour mieux comprendre les techniques de l'opération mathématique.

Raisonnements impliqués et apprentissages attendus:

Faire une soustraction, c'est enlever une quantité. J'aurai moins de choses qu'avant.

Activités préalables

Préciser le sens de la soustraction en demandant aux personnes des exemples dans leur quotidien et en utilisant de l'argent ou des objets pour les illustrer. En général, les gens vont donner des exemples avec de l'argent

Matériel nécessaire

• Des objets regroupés en paquets de 100, de 10 et à l'unité
• Des cartons rectangulaires d'environ 60 par 20 cm

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• travaille avec les objets devant les participantes et participants;
• utilise des situations concrètes de soustraction en tenant compte du sens.

Il est préférable de travailler un sens à la fois en commençant par le sens premier.

Nous avons semé 386 plants de fleurs et de légumes. Nous en avons vendu 254.

• Combien reste-t-il de plants?

Illustrons les données:
386, c'est trois verres de 100, huit verres de dix et six unités.

[Voir l'image pleine grandeur]

Placer les verres sur le carton, puis descendre sous la ligne (définie par une règle ou une bande de papier) la quantité (254) de plants vendus. Il reste en haut ce qui n'a pas été vendu.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur:

• demande aux participantes et participants de faire la même chose sur leur carton en utilisant des objets et d'autres nombres. On s'en tiendra d'abord aux soustractions simples sans emprunt

Puis, on reprend le problème sous une autre forme.

Nous avions 386 plants. Il reste 132 plants.

• Combien avons-nous vendu de plants?

Il faut isoler (descendre ou sortir du carton) 132 pour voir ce que nous avons vendu.

En travaillant la même situation, nous pouvons voir comment la soustraction peut aider à résoudre ce problème.

Deuxième étape

Les gens travaillent avec des dessins seulement, soit au tableau soit sur une feuille. Ils trouvent des situations de soustraction.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur pose des questions:

• Combien as-tu de verres maintenant?
• Quelle opération as-tu fait?

En calcul, lorsqu'on enlève une quantité à une autre quantité, on donne un nom à cette action ou opération: c'est une soustraction. On dit qu'il faut soustraire.

On peut dire aussi faire un moins. C'est le signe - qui indique la soustraction.

Troisième étape, le passage à l'écriture algorithmique

L'animatrice ou l'animateur:

• propose le problème de soustraction;
• place ensuite dans les grilles dessinées au tableau les dessins et les chiffres comme ci-dessous et explique chaque façon de représenter la soustraction.
  Chaque grille, bien que différente, représente la même chose.

[Voir l'image pleine grandeur]

Quatrième étape

On demandera ensuite à une personne de refaire la même chose au tableau en choisissant l'une des quatre façons de faire. Puis une autre personne ira à son tour en utilisant une autre façon de procéder et ainsi de suite. On compare ensuite les méthodes et les réponses pour se rendre compte que le résultat est toujours le même.

On peut expliquer le zéro dans la soustraction à l'aide des grilles et des verres. Plusieurs personnes rencontrent des difficultés à ce niveau. Il s'agit de faire comprendre que le zéro indique l'absence d'un groupe et n'annule pas le reste de la soustraction (six moins zéro donne six et non zéro).

Durée de l activité: deux heures

Imprimer l'exercice complet

Activité 2 - «Peux-tu me prêter un dix?» [...]

«Peux-tu me prêter un dix?», ou l'art d'emprunter

Objectif de l'activité

Faire découvrir les techniques de la soustraction avec emprunt.

Difficultés que pose l'activité

Nous devons revenir, comme il a été dit précédemment, aux notions de regroupement et de valeur positionnelle pour expliquer l'emprunt. Il faut de plus faire abstraction de la situation réelle devant un calcul écrit. L'exemple suivant montre la différence entre la soustraction mathématique et ce qui se passe dans la réalité.

Paul a 45$. Son épicerie coûte 18$. Pour payer, il utilisera un billet de 20$ ou deux billets de 10$. Jamais il ne sera question du nombre 15 (15 - 8) ou (8 + = 15) comme dans la soustraction écrite 45 -18. De là vient la difficulté à comprendre la soustraction et aussi à mémoriser les soustractions de base.

Raisonnements impliqués et apprentissages attendus:

• Reconnaître la valeur positionnelle des chiffres.
• Comprendre le sens de l'emprunt

Activités préalables

• Travailler sur les petits nombres. Faire compléter jusqu'à...: j'ai 15 lettres à poster, j'ai seulement huit timbres.
• Avec des sous noirs et des dix sous ou encore des paquets de 10 et des unités, enlever une quantité qui demande de transformer la dizaine en unités.

Matériel nécessaire

• Un sac de jetons
• Un carton de 60 par 20 cm
• Des grands verres et des petits verres

Déroulement: les étapes

Première étape

L'animatrice ou l'animateur:

• présente le problème de soustraction:

J'ai 443 jetons.
J'enlève 126 jetons.

• Combien reste-t-il de jetons dans le grand sac?
• Quelle opération faut-il faire?
• explique et fait d'abord la démarche elle-même à l'aide des verres.

Dans mon sac, j'ai 443 jetons, c'est-à-dire:
quatre grands verres de 100, quatre petits verres de 10 et trois jetons.

Je place les verres sur le carton.

[Voir l'image pleine grandeur]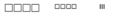

Je dois enlever 126 jetons, c'est-à-dire:
un grand verre de 100, deux petits verres de 10 et six jetons.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur:

• commence par les centaines, puis les dizaines pour montrer qu'aux unités, ça ne se passe pas de la même façon;
• demande comment on peut regrouper autrement les jetons pour avoir le même nombre et enlever les six jetons;
• laisse les gens discuter et trouver leurs solutions.

Deuxième étape

L'animatrice ou l'animateur:

• dessine la grille au tableau et reproduit le cheminement effectué lors de la manipulation avec les verres, ce qui donne une grille semblable;
• explique et montre chacun des dessins: j'ai quatre groupes de 100 et je dois en enlever un. J'ai quatre groupes de 10, je dois en enlever deux. J'ai trois jetons à l'unité et je dois en enlever six.

[Voir l'image pleine grandeur]

Il faut veiller à ce que les gens comprennent bien le pourquoi de cette disposition: dans les cases du haut, j'ai le nombre de jetons initial, et dans les cases du bas, le nombre de jetons que je dois enlever (voir commentaires plus loin). C'est ici que réside l'avantage mais aussi la difficulté du calcul écrit: il faut noter toutes les données. (L'exemple suivant peut être raconté et même essayé en groupe: dans certains pays, le calcul se fait oralement Ainsi, lors de transactions complexes, le compteur du village demande aux gens regroupés en cercle autour de lui de retenir le résultat partiel de ses calculs. Il peut y revenir quand c'est nécessaire en demandant à la personne de lui dire quelle réponse il lui avait demandé de retenir.)

L'animatrice ou l'animateur:

• calcule chaque colonne (en commençant par les centaines, on obtiendra une réponse approximative);
• explique que le chiffre du bas indique que je dois enlever un groupe de 100;
• barre un grand carré en haut;
• écrit la réponse sous la colonne: il en reste trois;
• fait de même avec les dix;
• écrit la réponse sous la colonne: il en reste deux;
• fait remarquer qu'il y a moins d'unités dans la case du haut et qu'il faut aller en chercher ailleurs (se rappeler la manipulation);
• emprunte un groupe de 10;
• barre le 2 et écrit 1 sous le 2;
• transporte «le groupe de 10» dans la colonne de droite et barre six jetons;
• écrit la réponse sous la colonne: il en reste sept

Voir la vidéo pour un exemple concret de cette façon de faire.

L'animatrice ou l'animateur:

• refait le calcul en commençant par les unités pour démontrer que le résultat est le même.

Après quelques exemples, on reprend la même démarche avec les nombres seulement.

Voici des exemples de représentations qui préparent la dernière étape sans le support de la grille.

[Voir l'image pleine grandeur]

Troisième étape

Les participantes et participants refont le même exercice avec d'autres nombres et d'autres problèmes pratiques.

Durée de l'activité: deux heures et plus

Commentaires généraux sur la soustraction

À partir de cette expérimentation, nous avons constaté qu'il n'est pas facile d'enseigner la soustraction si l'on s'en tient à des situations détachées d'expériences concrètes et immédiates. Il faut même placer les personnes dans des situations réelles où elles devront découvrir le sens de la soustraction et effectuer des opérations qui leur permettront de résoudre le problème. Le concept de la soustraction est difficile à comprendre. Il se découvre peu à peu par l'expérience, car selon les situations, le référent change; on peut même se retrouver avec deux groupes de référence comme dans les cas de comparaison. Cette notion ne se développera que si les participantes et participants ont procédé à des expériences pertinentes de manipulation.

Par conséquent, c'est dans un contexte bien défini que les exercices qui précèdent doivent être faits et expliqués. On retrouve d'ailleurs plusieurs occasions où la reconnaissance de la soustraction est nécessaire pour trouver la solution aux problèmes dans les activités d'enrichissement et d'approfondissement.

Les exercices visent aussi à aider certaines personnes à mieux comprendre ce qu'elles ont appris à faire mécaniquement, ou encore à découvrir la relation entre la soustraction et son expression numérique, expression qui peut amener une certaine confusion.

Par exemple, une personne ne pouvait comprendre que les nombres puissent se soustraire les uns des autres. Son expérience lui disait que lorsqu'elle «enlevait de l'argent ou des choses», il n'y avait qu'un montant ou qu'un nombre en jeu. On a pu voir jusqu'où allait la confusion lorsqu'on lui a demandé d'effectuer au tableau la soustraction 149 - 57. Cette personne a effacé le 7 quand on lui a dit: «il faut enlever 7». Pourtant, présentée d'une autre façon, elle a pu réussir la soustraction sans problème.

Voici la représentation qui rappelle le plus le modèle de l'argent:

• j'ai 100 40 9;
• j'enlève 50 7;
• je prends 50 sur 100, et 7 sur 9;
• il me reste 50 + 40 + 2, soit 92.

Pour d'autres personnes, toutes ces techniques deviennent un charabia inutile qui ne vient que les «mêler» davantage. Elles demandent qu'on leur montre la technique étape par étape. Il faut résister à cette tentation ou alors revenir sur l'opération globale, sinon on détruit toute la portée pratique du travail.

De plus, il existe plusieurs méthodes de soustraction. On peut soustraire en soustrayant mais aussi en additionnant. On peut le faire de haut en bas ou de bas en haut. Par exemple, 15 - 8 se dit quinze moins huit, ou huit de quinze. On peut aussi passer par le 10, soit de 8 à 10 (deux) et 10 à 15 (cinq), pour donner 7, etc.

En fait, les difficultés sont tellement grandes pour les personnes qui ne sont pas familiarisées avec les nombres et les principes de la numération qu'il ne faut pas abuser des exercices techniques de soustraction. On peut facilement y consacrer un temps considérable, qu'il vaudrait mieux utiliser à autre chose et se servir de la calculatrice qui, dans certains cas de calculs complexes, représente un outil tellement plus rapide et plus sûr.

Cependant, si on introduit trop tôt la calculatrice, on risque de court-circuiter l'apprentissage. L'animatrice ou l'animateur doit prendre le temps d'expliquer aux participantes et participants le rôle néfaste que peut avoir la calculatrice. En se fiant seulement à cet outil, on s'empêche de développer le sens des opérations et de découvrir des méthodes de calcul qui peuvent parfois s'avérer très simples.

Imprimer l'exercice complet

La multiplication

[Voir l'image pleine grandeur]

Activité 1 - Des boîtes de conserve, ça se multiplie ou ça s'additionne

Objectif de l'activité

Amener les participantes et participants à découvrir que l'on peut réunir le même nombre d'objets de même valeur en différents groupes afin d'accélérer le calcul de la somme.

Difficultés que pose l'activité

Les personnes participantes ont déjà vu le concept de multiplication à l'école, mais elles n'en ont retenu habituellement que l'aspect calculatoire, rattaché strictement au souvenir d'un exercice de mémorisation rigoureux et très exigeant C'est pourquoi elles abordent souvent avec une grande crainte la multiplication.

Raisonnements impliqués et apprentissages attendus:

• Comme les objets, les nombres se classent par groupes.
• Les objets et les nombres regroupés s'additionnent plus facilement et plus rapidement.
• Addition répétée = multiplication.

Activités préalables

Les participantes et participants doivent connaître les concepts d'addition et de soustraction.

Matériel nécessaire

Des boîtes de conserve

Déroulement: les étapes

Première étape, en grand groupe

L'animatrice ou l'animateur:

• présente quatre boîtes de conserve d'une valeur de 2$ chacune:

[Voir l'image pleine grandeur]

• demande aux participantes et participants de trouver la valeur totale en argent.

Par la suite, on complexifie l'opération en rajoutant d'autres boîtes à acheter:

• Combien coûteraient huit boîtes? Dix boîtes?, etc.

Il devient alors plus difficile d'additionner toutes les boîtes l'une après l'autre sans perdre le. compte. On rendra le calcul plus aisé en regroupant les boîtes par groupes de deux, quatre ou cinq. Certaines personnes devraient alors avoir procédé par regroupement.

Quand une ou plusieurs personnes entreprennent le processus de regroupement, on compare les méthodes de calcul de chacune. Il faut bien veiller à ce que les personnes concernées fassent ressortir les avantages du regroupement. On compare et on discute.

On reprend avec d'autres exercices de calcul à addition répétée en demandant aux participantes et participants d'essayer de calculer, par regroupement, d'autres boîtes de conserve à 2, 3, 4 ou 5$. Il serait sans doute intéressant de jumeler les personnes à ce stade.

On procède à d'autres exercices de calcul à addition répétée en manipulant d'autres objets que des boîtes de conserve.

Deuxième étape, en grand groupe

L'animatrice ou l'animateur:

• présente les problèmes avec les boîtes de conserve (ainsi que d'autres problèmes proposés auparavant) au tableau. Elle ou il demande aux participantes et participants de trouver le total en regroupant les objets en fonction des prix.

Le tableau sert de transition avant de passer au crayon et à la feuille de papier. Il s'agit de reproduire graphiquement le processus de regroupement. Ces exemples peuvent plus tard être reproduits sur papier et travaillés individuellement, au moment où l'animatrice ou l'animateur le jugera propice.

Durée de l'activité: deux heures

Imprimer l'exercice complet

Notes et commentaires

Le but de cet exercice n'est pas de faire en sorte que les participantes et participants sachent tout de suite, par exemple, que huit boîtes de conserve à 2$ chacune coûtent 16$ parce que 8 x 2 = 16, mais plutôt de leur faire découvrir que lorsqu'on a plusieurs éléments de même valeur à additionner, on peut les regrouper pour en trouver plus facilement la somme. En d'autres mots, on amène les participantes et participants à reconnaître les conditions d'utilisation de la multiplication que l'on fera découvrir en introduisant, lors du prochain exercice, le mot «fois».

Activité 2 - Donner un sens au mot «fois»

Objectif de l'activité

Amener les participantes et participants à découvrir que l'on peut réunir le même nombre d'objets de même valeur en différents groupes afin d'accélérer le calcul de la somme.

Difficultés que pose l'activité

En principe, on ne devrait pas rencontrer de difficulté à cette étape. Si certaines personnes ont de la difficulté à regrouper et calculer au tableau, on reviendra aux manipulations des boîtes de conserve.

Raisonnements impliqués et apprentissages attendus:

• Comme les objets, les nombres se classent par groupes.
• Les objets et les nombres regroupés s'additionnent plus facilement et plus rapidement.
• Addition répétée = multiplication.

Activités préalables

Les participantes et participants doivent connaître les concepts d'addition et de soustraction.

Matériel nécessaire

Des dessins au tableau

Déroulement: en une étape

L'animatrice ou l'animateur:

• présente des problèmes au tableau avec des séries d'additions de boîtes de conserve qu'il faut regrouper et dont il faut trouver l'équivalence en équation de multiplication.

$4 + $4 + $4 + $4 + $4 =$20
5 fois $4 = 20$

C'est à cette étape que l'on introduit le symbole graphique «X» pour représenter la multiplication dans une opération. Il s'agit d'introduire l'idée que les additions de groupes de même valeur peuvent être représentées graphiquement par une multiplication.

• demande aux participantes et participants de trouver des situations dans la vie où la multiplication peut s'appliquer.

Le même type d'exercices est par la suite présenté sur papier.

Durée de l'activité: une heure

Imprimer l'exercice complet

Notes et commentaires

Cette activité consiste à distinguer, à l'oral puis à l'écrit, le concept de la multiplication de celui de l'addition. On le fait à partir de l'opération que les participantes et participants connaissent et qui ressemble à la multiplication, c'est-à-dire l'addition.

Il faut évidemment démontrer que la multiplication ne peut s'appliquer que lorsqu'il y a addition d'éléments de même valeur. Lorsque les éléments à additionner ne sont pas tous de la même valeur, on ne peut qu'additionner.

Activité 3 - Les conditions d'utilisation de la multiplication

Objectif de l'activité

Amener les participantes et participants à découvrir que l'on ne peut regrouper que des objets de même valeur pour pouvoir utiliser la multiplication.

Difficultés que pose l'activité

On aurait avantage à utiliser le modèle de l'argent pour introduire cette activité. En général, les personnes utilisent cette méthode de regroupement. Elles regroupent pour mieux calculer les billets de 20$, les billets de 10$,etc. Il faut leur faire remarquer que la même méthode peut s'appliquer dans la situation ci-après.

Raisonnements impliqués et apprentissages attendus:

• Comme les objets, les nombres se classent par groupes.
• Les objets et les nombres regroupés s'additionnent plus facilement et plus rapidement.
• Addition répétée = multiplication.

Activités préalables

Vérifier à l'aide de billets de banque comment les gens classent et calculent l'argent

Matériel nécessaire

Des dessins représentant des boîtes de conserve

Déroulement: les étapes

Première étape, en grand groupe

L'animatrice ou l'animateur:

• reprend l'exemple des boîtes de conserve à l'oral avec différents scénarios:
  - On va acheter chez l'épicier des boîtes de conserve de prix parfois différents et parfois semblables. Quand peut-on regrouper et multiplier? Quand doit-on additionner chacune des boîtes?

Deuxième étape, en grand groupe

L'animatrice ou l'animateur:

• présente les problèmes des boîtes de conserve de même valeur ou de valeurs différentes au tableau. Quand peut-on regrouper et multiplier?

[Voir l'image pleine grandeur]

• présente au tableau d'autres problèmes avec d'autres objets;
• demande de verbaliser: j'ai sept boîtes de 2$ ou sept fois 2$.

Les exemples sont reproduits plus tard sur papier et travaillés individuellement.

Imprimer l'exercice complet

Activité 4 - La table de multiplication

Objectif de l'activité

Faire construire et comprendre la table des multiplications. Cette activité doit se dérouler sur plusieurs semaines (environ six). Il ne faut pas chercher à remplir la table au complet en une seule fois, car les gens ne s'en souviennent pas. Aussi, tout en montant la table de multiplication, on intercale d'autres activités comme celle du «bingo» présentée ci-après.

Difficultés que pose l'activité

En principe, les participantes et participants ont déjà travaillé la multiplication dans son sens d'addition répétée. Les exercices où il faut compter par 2, 3, 4, 5, etc. sont d'une certaine façon aussi proches de la multiplication. La configuration rectangulaire ou l'aire n'est pas en réalité une nouvelle notion. Elle se présente plutôt comme une régularité, un arrangement différent qui aboutit à des opérations de multiplication. L'activité suivante va permettre de découvrir les propriétés de la multiplication en même temps que l'opération elle-même.

Raisonnements impliqués et apprentissages attendus:

• Comme les objets, les nombres se classent par groupes.
• Les objets et les nombres regroupés se calculent plus facilement et plus rapidement.

Activités préalables

On demande aux personnes participantes de chercher et d'apporter des objets regroupés de différentes façons pour illustrer la table de multiplication jusqu'à 9 ou 12 (boîtes d'œufs, cartes de boutons...). On veille à ce que toutes les combinaisons soient représentées.

Matériel nécessaire

• Un grand carton quadrillé 10 sur 10, ou 13 sur 13 si on va jusqu'à 12.
• Des objets regroupés ou classés de toutes sortes de façons (cartes de boutons, douzaines d'œufs, dosettes, empaquetages de jus, de liqueurs, de bonbons, etc.) Vous trouverez un grand nombre d'exemples dans la vidéo La sauce à... calculer.
• Un carton de boutons placés sans ordre ni regroupement

Déroulement: les étapes

Première étape, travail en équipe

L'animatrice ou l'animateur:

• distribue au hasard les objets entre les équipes;
• laisse les personnes les examiner et dire ce qu'elles voient et reconnaissent (après quelques minutes, les équipes échangent entre elles les objets reçus et poursuivent l'observation);
• poursuit l'activité en grand groupe par une mise en commun et en suscitant différentes observations:

- il existe des regroupements différents qui donnent le même nombre: 6 x 2 et 3 x 4 par exemple;
- quatre groupes de cinq et cinq groupes de quatre contiennent la même quantité;
- deux groupes de six et trois groupes de six réunis font cinq groupes de six, etc.

Deuxième étape, en grand groupe

L'animatrice ou l'animateur:

• montre le carton de boutons désordonnés et un arrangement ordonné;
• amène les participantes et participants à constater qu'il est plus facile d'en connaître le nombre si les objets sont regroupés dans un certain ordre.

Troisième étape

L'animatrice ou l'animateur:

• explique que toutes les combinaisons de multiplication sont représentées par les objets sur la table;
• qu'on peut transcrire en nombres sur un tableau toutes les données et tous les résultats pour mieux les retenir,
• présente le grand carton et explique la disposition.

Quatrième étape

Il s'agit d'entreprendre la construction de la table de multiplication sur un grand carton.

L'animatrice ou l'animateur:

• demande à une personne de choisir un regroupement et d'expliquer la disposition ou l'ordre du regroupement (dosette).

Il existe sept jours et trois cases par jour, ce qui donne 21 cases. Il faut ensuite écrire le résultat sur le carton au point de rencontre du 3 et du 7. Puis, on écrit au tableau sans référence aux objets: 3x7 =21; 7x3=21

On poursuit l'exercice de la même façon pour compléter le tableau.

Durée de l'activité: trois heures ou plus

Notes et commentaires

On peut facilement s'embrouiller dans l'explication de la disposition du regroupement. Certaines situations ne permettent pas toujours d'inverser les nombres sans en changer le sens. Il faut donner la situation telle qu'elle se présente: il y a quatre boutons par rangées, il y a cinq rangées, ce qui fait 20 boutons. On reprend ensuite avec les nombres seulement: 4 fois 5 font 20 et 5 fois 4 font aussi 20.

L'animatrice ou l'animateur devra prendre garde de ne pas utiliser le «multiplier par» et le «fois» comme des synonymes. Il faut les distinguer: 5 fois 4 = 4 multiplié par 5. C'est la notion de «fois» qu'il faut consolider chez les participantes et les participants.

Certaines personnes auront de la difficulté à repérer la bonne ligne et la bonne colonne pour inscrire le résultat. On peut se fabriquer une équerre qui servira de repère.

On peut coller sur le grand carton quadrillé des bandes de «Velcro». On découpe ensuite des petits carrés sur lesquels seront inscrits les résultats des multiplications. À l'endos des petits carrés, on colle aussi un morceau de Velcro.

Au lieu d'écrire le résultat sur le carton, on va coller le petit carré à la bonne place. On aura préalablement distribué tous les carrés entre les participantes et participants.

Par la suite, le tableau peut devenir un jeu. On enlève toutes les réponses qu'il faut replacer à tour de rôle. On peut se donner des consignes: remplir une colonne, une rangée, une diagonale, placer un petit carré et trouver toutes les réponses qui vont autour, placer un carré sur le jeu et, à tour de rôle, placer un carré qui touche à celui ou ceux déjà en place, etc.

Le bingo pour mémoriser les tables

Le jeu de bingo est un moyen amusant et efficace pour aider les personnes participantes à mémoriser les tables. Il est facile et de fabrication peu coûteuse. De plus, c'est un exercice que les gens aiment beaucoup pratiquer. Il faut pour cela reproduire plusieurs exemplaires de la carte reproduite à la page 72. Les tables de 4, 6, 7, 8 et 9, qui causent plus de difficultés, sont utilisées pour cet exemple. On peut cependant construire le même jeu avec les tables de 2, 3, 4, 5 et 6.

Il s'agit tout simplement pour l'animatrice ou l'animateur d'inscrire les produits des multiplications dans les colonnes pertinentes et dans un ordre différent sur chaque carte (sinon, tout le monde fera un «bingo» en même temps). Il est bien évident qu'on ne retrouvera pas toutes les réponses des combinaisons sur une même carte (voir l'exemple de carte remplie).

Puis, sur des cartons d'environ un pouce carré, l'animatrice ou l'animateur inscrit toutes les suites de multiplication correspondant aux tables choisies. Par exemple, si on travaille avec les tables de 4, 6, 7, 8, 9, il faut faire des cartons pour toutes les séries de multiplication: 4 x 2, 4 x 3, 4 x 4, 4 x 5... 4 x 12, puis 6 x 2, 6 x 3, 6 x 4, et ainsi de suite pour les tables de 7, 8 et 9. On devrait se retrouver avec 55 cartons pour ces tables, en supposant que l'on n'en ait pas fait pour le « X » fois 1.

Le jeu est maintenant prêt. Celui ou celle qui connaît toutes ses tables par cœur et qui donne toutes les réponses avant les autres sera le maître du jeu. Les petits cartons sont placés dans un sac en papier pour que les gens «pigent» au hasard. Le maître du jeu sort un carton et annonce: «Dans les colonnes des 7, 7 fois 8.» Les gens cherchent sur leur carte si la réponse de 7 fois 8 s'y trouve et placent un jeton dans la case s'il y a lieu.

Il faut bien veiller à choisir la bonne colonne car la réponse 56 peut se retrouver dans la colonne des 7 (7 x 8) et dans la colonne des 8 (8 x 7).

Comme c'est un jeu, les gens peuvent s'aider, se donner la réponse, utiliser leur table ou la calculatrice pour trouver le résultat.

Toutes les dispositions possibles peuvent être acceptées pour faire bingo: en lignes horizontales, verticales, en diagonales. On peut aussi faire des lettres: le H, le L, le N. Les personnes connaissent en général tous les trucs et vous diront comment faire si vous ne le savez pas. Bonne chance, le jeu commence: dans la table de 7, 7 fois 9...

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Activité 5 - La multiplication des nombres [...]

La multiplication des nombres plus grands que 10 par un nombre plus petit que 10

Objectifs de l'activité

Introduire la multiplication des grands nombres.
Amener les gens à faire des comparaisons entre les techniques de l'addition et de la multiplication.
Introduire la disposition verticale pour la multiplication.

Difficultés que pose l'activité

La multiplication suppose qu'on ait bien compris les principes de la numération et du regroupement. En travaillant avec le carton utilisé lors des activités consacrées au dénombrement et à l'addition, on facilite le transfert et l'acquisition de cette nouvelle notion.

Raisonnements impliqués et apprentissages attendus:

• Les objets et les nombres regroupés s'additionnent plus facilement et plus rapidement.
• Addition répétée = multiplication.
• Développer un nouveau degré d'abstraction: un jeton de telle couleur équivaut à dix et un jeton de telle autre couleur équivaut à une unité.

Activités préalables

Les personnes participantes doivent connaître les concepts d'addition.

Matériel nécessaire

• Cartons rectangulaires de 20 par 60 cm
• Jetons de couleurs différentes (des jetons de bingo de couleur rouge, bleu ou orange font très bien l'affaire)
• Des verres de deux tailles différentes

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, en deux équipes

L'animatrice ou l'animateur:

• distribue à chaque personne un carton et des jetons de couleurs différentes (des bleus pour les dizaines et des rouges pour les unités), ainsi que des verres de deux grandeurs différentes, du papier et des crayons;
• présente un problème avec des nombres supérieurs à dix.

Le marchand reçoit ses conserves en caisse de 24.
Hier, il a reçu trois caisses de pois verts.

- Combien y a-t-il de boîtes de conserves?
- Comment l'illustrerais-tu?

• demande d'illustrer le problème sur le carton ou d'une autre façon, soit par un dessin soit à l'aide des verres.

Ultimement, on devrait aboutir à la représentation ci-dessous. Cependant, certaines personnes ne seront pas nécessairement prêtes à passer à ce stade d'abstraction. Il faudra laisser les gens recourir aux verres et aux dessins si nécessaire, mais on devra encourager cette façon de représenter le problème.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur:

• pose des questions:

- Quelle opération avez-vous faite pour résoudre le problème?
- Peut-on utiliser une autre opération que l'addition?
- Laquelle? Pourquoi?
- Voyez-vous trois fois 24 sur un carton?

Il faut demander aux gens de décrire ce qu'il y a sur le carton.

Il faut les amener à dire que 3 x 24, c'est la même chose que trois fois 20 plus trois fois quatre.

On écrit au tableau:

[Voir l'image pleine grandeur]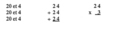
Deuxième étape

L'animatrice ou l'animateur:

• demande aux participantes et participants de composer des problèmes semblables et de les illustrer à leur façon. S'il y a trop peu de manières différentes qui ressortent, l'animatrice ou l'animateur en propose d'autres et les fait comparer.

Troisième étape

Il s'agit de faire les opérations par écrit.

Durée de l'activité: trois heures

Imprimer l'exercice complet

Notes et commentaires

L'utilisation du carton permet d'effectuer des opérations de multiplication avec de grands nombres. Cette méthode comporte plusieurs avantages: elle permet, entre autres, d'expliquer la technique opératoire en montrant les ressemblances avec l'addition. Les personnes moins avancées peuvent réussir des opérations qui seraient plus difficiles autrement. Enfin, cette façon de procéder vient renforcer le concept de la numération.

La division

[Voir l'image pleine grandeur]

Objectifs des activités

• Amener les participantes et participants à comprendre le sens de la division (séparer en parties distinctes, répartir également).
• Faire découvrir que l'on peut séparer un ensemble d'éléments de même valeur, dans différents groupes, pour en faciliter le calcul.
• Faire pratiquer l'algorithme de la division par ceux et celles qui le connaissent déjà.
• Amener les participantes et participants à établir la relation qui existe entre la division et la multiplication.
• Faire découvrir des «méthodes de division commodes» dans la vie courante.

Note

La division est présentée dans ce chapitre comme une opération mathématique impliquant un raisonnement mathématique. En effet, dans la vie courante, plusieurs divisions peuvent se faire sans algorithme. Souvent, «à l'école», on montre un algorithme, simple procédure mécanique à suivre, sans qu'on se préoccupe du sens de l'opération à effectuer. Aussi vous ne trouverez pas, dans les pages qui suivent, d'introduction à l'algorithme comme tel parce qu'on ne veut pas que la division soit comprise, par les adultes, comme une simple procédure de calcul.

En plus, nous avons choisi de présenter des problèmes qui sont exclusivement des opérations de division simple, à un chiffre. Les problèmes présentant des divisions à deux chiffres ont trait exclusivement à l'argent, parce que ce sont des problèmes que les gens ont l'habitude de résoudre dans leur vie quotidienne.

Difficultés que posent les activités

Les personnes qui apprennent le calcul font des divisions. Dans son sens de partage, il leur est facile de trouver la moitié ou partager en deux. Elles sauront aussi distribuer également entre plusieurs personnes un certain nombre d'objets (un à chacun, jusqu'à épuisement des objets).

La division a aussi un sens de mesure et de contenance. C'est la division qui est utilisée quand on cherche combien il y a de 5¢ dans un rouleau de 2$, combien de personnes on peut nourrir avec 58 sandwichs en donnant deux sandwichs à chaque personne, combien de sacs de 200 gr on peut faire avec un kilo (1000 gr) d'arachides. Les gens ne comprennent pas automatiquement la division quand on leur demande de changer un billet de 100$ en billets de 20$ ou de 10$. Pourtant, cela fait appel au sens de mesure de la division. De plus, lorsqu'ils constatent qu'ils ont divisé, le transfert du raisonnement qu'ils ont utilisé n'est pas facile à faire (voir La sauce à... calculer).

En outre, les participantes et participants auront de la difficulté à comprendre le sens de la division quand il s'agit de trouver le prix à l'unité, la moyenne d'âge d'un groupe ou encore le taux horaire d'un salaire.

Raisonnements impliqués et apprentissages attendus:

• Pour aborder l'algorithme de la division, il faut avoir acquis un minimum d'habiletés dans la résolution de l'addition, de la soustraction et de la multiplication. C'est aussi une opération où les erreurs de technique et de calcul sont grandes.
• Il faut amener les participantes et participants à voir la division comme l'inverse de la multiplication et à découvrir les relations entre ces deux opérations. Des exercices doivent être faits en ce sens.

Activités préalables

Les personnes participantes doivent connaître le concept de la multiplication, l'utilisation de la table de multiplication ainsi que celle de la calculatrice. Elles doivent également pouvoir illustrer les opérations mathématiques qu'elles effectuent.

Activité 1 - Le sens de la division

Objectif de l'activité

Amener les participantes et participants à identifier le sens de la division (séparer en parties distinctes, répartir également).

Matériel nécessaire

Aucun

Déroulement: les étapes

Première étape, en sous-groupe

L'animatrice ou l'animateur demande aux participantes et participants:

• d'identifier quelques situations de leur vie quotidienne où ils «séparent», répartissent des chose.

Exemples: habituellement, les gens divisent leur lavage selon certains critères(couleurs, degré de saleté); aux repas, les gens répartissent les portions selon le nombre de personnes qui mangent; lors d'un anniversaire, on coupe le gâteau en portions, etc.

• de nommer des situations, dans la vie, où des éléments sont «séparés».

Exemples: les tiroirs d'une commode séparent les vêtements; le jeu de tic-tac-to qui est séparé en cases; une épicerie qui est séparée en sections; un hôpital qui est séparé en étages, en chambres; un ensemble (set) de vaisselle qui est séparé en tasses, assiettes, soucoupes, bols à soupe, etc.

Deuxième étape, en grand groupe

L'animatrice ou l'animateur:

• invite chaque équipe à donner les exemples qu'elle a trouvés;
• inscrit ces exemples au tableau;
• apporte, si ce n'est pas fait par les participantes et participants, des exemples où la notion «d'égalité» dans la division est importante (Exemples: si un groupe gagne à la loto, on va diviser le montant en parts égales entre les gagnants; des co-locataires se partagent le coût d'une facture, etc.);
• à la suite des exemples, précise avec les participantes et participants, le sens de la division d'un point de vue mathématique.

Imprimer l'exercice complet

Activité 2 - Les conditions d'utilisation de la division

Objectif de l'activité

Faire découvrir que l'on peut séparer des éléments de même valeur en différents groupes égaux, pour en faciliter le calcul.

Matériel nécessaire

Deux centaines de dépliants publicitaires de l'organisme

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur dépose des dépliants publicitaires de l'organisme sur une table et énonce le problème suivant:

• J'ai 200 feuillets publicitaires à distribuer. Quatre personnes se sont portées volontaires pour les diffuser, porte à porte, dans leur quartier.
• Comment vais-je procéder pour séparer mes dépliants entre ces quatre volontaires?

L'animatrice ou l'animateur invite les participantes et participants à lui soumettre leurs «solutions». Les diverses solutions sont inventoriées. Certaines personnes peuvent procéder par approximation, d'autres vont manipuler les dépliants en les répartissant en quatre piles distinctes, d'autres encore vont peut-être utiliser leur calculatrice.

Lorsque le groupe a fait le tour des solutions apportées, l'animatrice ou l'animateur reprend le problème, au tableau, en l'illustrant.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur demande aux gens du groupe de lui dire ce que l'on cherche à trouver, c'est-à-dire le nombre de dépliants que chaque personne aura à distribuer.

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur invite les gens à lui proposer les étapes qu'elle doit suivre pour résoudre mathématiquement le problème illustré.

Tout d'abord, il faudra échanger les centaines en dizaines parce que deux ne peut se séparer en quatre.

Ensuite, il s'agit de répartir les dizaines entre chaque personne.

[Voir l'image pleine grandeur]

Et ainsi de suite, jusqu'à ce que les 20 dizaines aient été séparées en quatre.

[Voir l'image pleine grandeur]

On arrive ainsi à voir que quatre personnes qui ont à se répartir 200 dépliants en reçoivent chacune 50. On vient d'effectuer une division: 200÷4 = 50.

Deuxième étape, travail en grand groupe

L'animatrice ou l'animateur invite les participantes et participants à lui proposer divers problèmes qui demandent l'utilisation de la division. Cela peut se faire en grand groupe ou encore en dyade. L'important est d'inciter les personnes à soumettre leur problème et d'en inviter d'autres à les résoudre au tableau, en utilisant l'illustration mathématique proposée par l'animatrice ou l'animateur, à la première étape, ou encore en faisant la démonstration par la manipulation.

Note: Il est important que les gens puissent exposer leur propre façon de procéder en la verbalisant. Cela permet, entre autres, de voir quel raisonnement mathématique ils utilisent.

Imprimer l'exercice complet

Activité 3 - Diviser dans la vie courante

Objectif de l'activité

Faire découvrir que l 'on peut séparer un ensemble d'éléments de même valeur en différents groupes, pour en accélérer le calcul.

Faire pratiquer l'algorithme de la division pour ceux et celles qui le connaissent déjà. Faire découvrir des «méthodes de division commodes» dans la vie courante.

Matériel nécessaire

• Réglettes de base 10
• Un certain nombre de problèmes pratiques, (un problème par feuille), distribués à chaque équipe

Déroulement: les étapes

Première étape, travail en dyade

Les personnes participantes se groupent deux par deux. Elles pigent au hasard un problème à résoudre. Chacune doit lire le problème et tenter de le solutionner en utilisant la division, soit en manipulant les réglettes, soit en illustrant son opération (par dessin, par illustration mathématique, peu importe), ou encore en utilisant la calculatrice. L'équipe doit résoudre son problème en gardant à l'esprit qu'il lui faudra expliquer verbalement de quelle manière elle a procédé, lors du retour en grand groupe à la fin de l'activité.

Voici des exemples de problèmes qui peuvent être soumis aux équipes.

1. Combien y a-t-il de 2$ dans un billet de 50$?
2. Il y a 12 paires de bottes à l'entrée du local. Combien de personnes sont arrivées?
3. Dans un pain carré, il y a 32 tranches. Combien de sandwichs peut-on faire avec ce pain?
4. Une femme doit ranger 150 rouleaux de fils. Chaque boîte de rangement qu'elle utilise peut contenir 15 rouleaux. Combien devra-t-elle utiliser de boîtes pour ranger ses 150 rouleaux?
5. Claudette a acheté 48 bières. Combien a-t-elle acheté de caisses de 12 bières?
6. La collecte de café a rapporté 160 pièces de 25¢. Pour les déposer à la banque, on doit les rouler. Dans chaque rouleau de 25¢, il y a 40 pièces. Combien de rouleaux va-t-on utiliser?
7. Un homme roule lui-même ses cigarettes, pour la semaine. Il en fabrique 300. Combien de paquets de 25 cigarettes roule-t-il par semaine?
8. Vingt-huit personnes se sont inscrites pour jouer aux cartes. Chaque table peut accueillir quatre personnes. Combien de tables faut-il prévoir pour accueillir ces 28 personnes?

Deuxième étape, en grand groupe

L'animatrice ou l'animateur:

• invite chaque équipe à énoncer le problème qu'elle avait à résoudre;
• invite chaque équipe à présenter «sa» ou «ses» solutions au problème, soit en les expliquant, soit en venant les solutionner au tableau;
• invite les autres équipes à donner leur point de vue sur la façon dont le problème a été solutionné.

Le but de cette étape est de faire prendre conscience que certaines manières de résoudre la division sont plus rapides que d'autres, même si elles impliquent un raisonnement similaire.

Imprimer l'exercice complet

Activité 4 - Les rapports entre la division et la multiplication

Objectif de l'activité

Amener les participantes et participants à établir la relation qui existe entre la division et la multiplication.

Matériel nécessaire

Un tableau de la table de multiplication (il peut être illustré sur un grand carton ou encore présenté sur acétate que l'on projette sur un mur du local).

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur présente le tableau de multiplication, comprenant les tables de 1 à 12.

Tableau de multiplication

[Voir l'image pleine grandeur]

Elle ou il fait une démonstration de son utilité potentielle dans le cadre de la division, à l'aide de l'opération suivante: 40 ÷ 8 = ? et qui permettra de trouver ? x 8 = 40

Deuxième étape, travail en équipe

• Premier temps L'animatrice ou l'animateur invite chaque équipe à inventer des opérations de divisions, sur le modèle proposé à la première étape.
• Deuxième temps L'animatrice ou l'animateur demande aux équipes «d'échanger» entre elles leurs opérations. Chaque équipe doit résoudre les opérations proposées.

Note: À la fin de l'activité, l'animatrice ou l'animateur pourrait reprendre les diverses opérations et en constituer une banque. Cette banque serait redistribuée au groupe lors d'un atelier subséquent et les gens seraient invités à la compléter à l'aide de la table de multiplication, par exemple.

Imprimer l'exercice complet

Activité 5 - Utiliser la table de multiplication pour diviser

Objectif de l'activité

Dans le but de favoriser l'utilisation de la table de multiplication comme outil de référence de calcul et de consolider la notion de la division nouvellement apprise, l'animatrice ou l'animateur invite les participantes et participants à solutionner une série d'opérations.

Matériel nécessaire

• Une table de multiplication pour chaque participante et participant
• Une série d'opérations de division, sans reste
• Une série de problèmes impliquant diverses opérations mathématiques, dont la division

Déroulement: les étapes

Première étape, en individuel ou en dyade

L'animatrice ou l'animateur présente une série d'opérations de division, sans reste, en invitant les gens du groupe à utiliser, pour les résoudre, la table de multiplication. Ces opérations pourraient servir à combler la banque de division, constituée à l'activité 4. L'animatrice ou l'animateur incite les participantes et participants à échanger leurs réponses respectives, en les amenant à vérifier celles de leur partenaire à l'aide de la table de multiplication.

Deuxième étape, en individuel ou en dyade

L'animatrice ou l'animateur distribue différents problèmes mathématiques au groupe. La consigne est la suivante:

1. Identifier ce qu'on cherche à savoir.
2. Trouver quelle opération mathématique serait la plus appropriée à utiliser.
3. Effectuer l'opération, à l'aide de la table de multiplication ou de la calculatrice.

Voici quelques exemples de problèmes à résoudre:

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

Troisième étape, en grand groupe

L'animatrice ou l'animateur:

• fait un retour sur les différents problèmes mathématiques soumis aux participantes et participants, en invitant le groupe à énoncer comment il aurait résolu le problème présenté;
• amène les gens à observer que, dans les problèmes mathématiques, plusieurs opérations sont sollicitées parce que souvent, il n'y a pas qu'un seul raisonnement impliqué dans la résolution de problème.

Imprimer l'exercice complet

Note

Les modèles 4 et 5 impliquent plusieurs opérations, comportent plus d'une solution possible et il existe plusieurs ordres selon lesquels les participantes et participants peuvent procéder; c'est pourquoi nous n'avons retenu que la deuxième piste: «Quel est ton raisonnement, quelle(s) question(s) dois-tu te poser?». Il faudra tenir compte de ce type de complexité et du «niveau en mathématiques» des participantes et participants lorsque ces types de problèmes seront abordés.

Partie 2: Des projets ou les mathématiques au quotidien

Les projets suivants offrent des exemples de manières d'aborder et de faire des mathématiques. Ils ont été choisis et expérimentés en fonction de leur caractère concret. Ils sont facilement adaptables et peuvent suggérer des idées nouvelles aux animatrices et animateurs qui les consulteront. Ce sont des projets à moyen et long terme que l'on peut suspendre en cours de route pour faire des exercices et des retours sur les apprentissages de base.

Une sortie

[Voir l'image pleine grandeur]

Une sortie

Le thème de la «sortie» est un exemple d'activité au cours de laquelle les personnes doivent utiliser leurs connaissances mathématiques pour résoudre un problème résultant d'une situation vécue.

Chaque année, le club social du groupe organise et finance en partie des activités et des sorties. Pour réaliser ces activités, les membres du club sont amenés à planifier, à négocier des contrats de location et à évaluer les coûts de réalisation.

L'organisation de ces activités était effectuée par un nombre restreint de personnes faisant partie du club social. Comme ces mêmes personnes se retrouvaient dans les ateliers de calcul, il a été convenu de reprendre l'exercice avec toutes les participantes et participants des ateliers de calcul.

C'est une occasion, pour les personnes participantes, de développer et d'approfondir leurs connaissances en mathématiques en reprenant en atelier les différentes phases de préparation de l'activité. Dans une première étape, il faut évaluer les coûts de la sortie en fonction du nombre de personnes qui vont participer à l'activité. Dans un deuxième temps, c'est-à-dire après la réalisation de l'activité, l'atelier aura à calculer les coûts exacts, à évaluer le résultat et le degré de satisfaction des gens.

Comme plusieurs personnes ont de la difficulté avec la lecture, le problème est proposé sous forme illustrée. Cette présentation a l'avantage de permettre aux gens de voir et de retenir plus facilement les données. Les opérations à résoudre sont multiples et présentées en fonction du niveau de chacun et chacune. Tant les personnes débutantes que les plus avancées peuvent y participer.

On met l'accent sur la verbalisation et la découverte du sens des opérations a effectuer. On encourage et on valorise les méthodes personnelles de calcul. Les tableaux et les listes ordonnées sont abondamment utilisés pour faciliter la résolution des problèmes.

Voici les éléments qui seront abordés dans le cadre de cette activité thématique:

• l'orientation dans l'espace et dans le local;
• la direction et les points cardinaux;
• la lecture d'une carte géographique;
• les quatre opérations de base;
• les taxes;
• les rapports, proportions et pourcentages;
• le kilométrage, les kilomètres et le mètre.

Objectifs généraux de ce thème

Calculer les coûts de la sortie et le montant que devra débourser le club social (ou le groupe).
Évaluer l'activité dans son ensemble.
Bonne sortie!

Activité 1 - Localiser le lieu de destination

Objectif de l'activité

Amener les gens à s'orienter dans l'espace.

Difficultés que pose l'activité

Nous avons retenu une sortie à la cabane à sucre pour illustrer la démarche. Nous verrons aussi comment utiliser au maximum une situation pour introduire les notions nouvelles et approfondir certains apprentissages.

Raisonnements impliqués et apprentissages attendus:

• L'orientation dans l'espace et dans le local.
• La direction et les points cardinaux.
• La lecture d'une carte géographique.
• Le kilométrage, les kilomètres et le mètre.

Activités préalables

• Déterminer une date.
• Faire un sondage pour savoir combien de personnes désirent participer à l'activité.
• Faire les démarches et arrêter son choix sur une cabane à sucre.
• Trouver la compagnie de transport qui offre les meilleurs prix.
• Fixer le prix demandé aux participantes et participants pour la sortie.

Matériel nécessaire

• Cartes géographiques; il s'agira ici de la carte de l'Ile d'Orléans
• Boussole, si possible
• Globe terrestre
• Règle d'un mètre

Déroulement: les étapes

L'animatrice ou l'animateur:

• présente la sortie et le lieu choisi;
• situe l'endroit par rapport au local (dans quelle direction allons-nous partir,référence aux rues et boulevards);
• situe les points cardinaux dans le local par rapport au soleil ou à l'aide de la boussole;
• présente la carte de l'Ile d'Orléans;
• situe la direction, le fleuve et ses rives, le pont, les paroisses, y compris celle où se trouve la cabane à sucre; • situe le lieu sur la carte du Québec ou du Canada;
• situe les points cardinaux sur la carte;
• dessine la rose des vents et indique les points intermédiaires: NO, NE, SO, SE;
• explique le kilomètre comme l'équivalent de 1000 règles d'un mètre placées bout à bout, ou de 10 minutes de marche rapide, ou la distance de tel point à tel autre.

Durée de l'activité: une heure et plus selon l'intérêt et les questions

Imprimer l'exercice complet

Notes et commentaires

Cette activité sur l'orientation et les points cardinaux a donné lieu à toutes sortes de questionnements sur les saisons, le mouvement de la terre ou le système solaire. Cela démontre l'intérêt des participantes et participants pour tout ce qui touche à l'astronomie, à la géographie et aux phénomènes naturels. Ce champ d'intérêt pourra être mis à profit et servir de thème dans les ateliers de français.

Avec les personnes moins avancées, pour qui la lecture d'une carte est plus difficile, on peut travailler l'orientation dans la salle en localisant les points cardinaux à partir de l'est.

Petit jeu d'orientation: les gens se placent debout soit seuls, soit face à face ou dos à dos. On leur demande de faire un quart, un demi ou trois quarts de tour sur eux-mêmes, puis de marcher droit devant eux. Ils doivent dire dans quelle direction ils vont.

Activité 2 - Analyse et étude du problème illustré

Objectifs

Amener les participantes et participants à choisir les données nécessaires à la résolution d'un problème.

Faire préciser les sens des opérations.

Amener les participantes et participants à faire des liens entre les quantités et les données en cause.

Difficultés que pose l'activité

L'une des principales difficultés rencontrées dans la résolution des problèmes réside dans la lecture et la compréhension des données. Pour aider les personnes à bien saisir et retenir ces données, pour les aider à mieux définir les opérations à effectuer, nous illustrons le problème. De cette façon, elles sont en mesure d'avoir une vue d'ensemble, de travailler à leur rythme et selon leur degré de connaissances.

Raisonnements impliqués et apprentissages attendus:

Après l'étude des données, les participantes et participants devront être en mesure de déterminer le montant que le club social devra défrayer pour le transport et le repas.

Activités préalables

Les personnes doivent connaître les concepts des opérations de base.

Matériel nécessaire

La feuille illustrée du problème et des crayons de couleur.

Déroulement: les étapes

Première étape

L'animatrice ou l'animateur:

• distribue la feuille et explique le sens des illustrations;
• donne les renseignements nécessaires;
• demande au groupe d'inscrire les données suivantes sous l'illustration correspondante.

Les données:
Nombre de personnes qu'on peut identifier comme suit: 12 participants, 17 participantes, cinq animatrices et trois enfants.

Les revenus:
Prix demandé par le club social:

• 8$ par personne
• Gratuit pour les enfants

Les dépenses:

Transport:

• Autobus: 120$ + taxes
• Auto: 0.15$ du kilomètre (Monique utilise son auto et amène trois personnes avec elle).

Le trajet jusqu'à la cabane à sucre est de 40 kilomètres.

Repas:

• 12$ par personne, taxes incluses
• Moitié prix pour les enfants

Sortie à la cabane à sucre

[Voir l'image pleine grandeur]

Deuxième étape, travail en grand groupe, oralement

Les données sont complétées et expliquées.

• Que représentent les petits personnages?
• Combien y en a-t-il? On regroupe pour calculer le nombre de personnes.

Avec des crayons de couleurs différentes, on identifie les animatrices, les participantes, les participants et les enfants.

• Que faut-il faire (opération) pour trouver le nombre de participantes et de participants seulement?

L'autobus:

• Pouvez-vous dire environ combien il faudra débourser pour les taxes si la TPS est de 7% et la TVQ de 6,5%?

L'auto:

Monique a utilisé son auto et a emmené trois personnes avec elle. Des flèches relient les personnages à l'auto.

• Que faut-il faire pour trouver combien de personnes ont fait le voyage en autobus?
• Pourriez-vous trouver quelle somme d'argent il faudrait débourser pour un trajet de 10, de 20, de 40, de 80 km?

Chaque adulte a payé 8$ pour le voyage.

• Combien de «8$» le club social a-t-il recueillis?
• Est-ce suffisant pour payer toutes les dépenses?
• Qu'est-ce qui peut être considéré comme un revenu, comme une dépense, dans ces données?
• Si le repas coûtait 10$, seriez-vous capable d'estimer le coût total des repas?
• Que faut-il faire pour trouver le prix du repas d'un enfant?
• Peut-on déterminer le montant que le club social devra payer?

Durée de l'activité: une heure trente minutes

Imprimer l'exercice complet

Notes et commentaires

L'exercice consiste à définir les opérations à effectuer et à en comprendre le sens. L'illustration montre l'ensemble de la situation. Tout le raisonnement et l'estimation des coûts se font d'abord à partir du tableau. Il ne s'agit pas de chercher la réponse, mais de trouver comment faire pour y arriver. Les questions doivent permettre de bien saisir les données, de faire des liens, d'établir des relations entre les quantités en cause (par exemple: 8$ par personne et 34 adultes).

Activité 3 - Calcul du coût de la sortie

Objectif

Amener les participantes et participants à décomposer un problème complexe en problèmes simples pour mieux le comprendre et le résoudre.

Difficultés que pose l'activité

Nous sommes en présence d'un problème complexe qui demande une série d'opérations. Après avoir analysé le problème, il faudra le décomposer en une série de problèmes simples. Pour décomposer, on peut soit partir des données (qu'est-il possible de trouver avec deux données et ainsi de suite jusqu'au résultat), soit partir de ce que l'on cherche (ce qu'il faut savoir pour être en mesure de calculer ce que demande le problème). La première démarche est un genre de tâtonnement qui se fait par essais; elle est plus facile. La seconde démarche exige que l'on fasse l'analyse de l'ensemble du problème et s'adresse aux personnes plus avancées.

Raisonnements impliqués et apprentissages attendus:

• Les quatre opérations
• Le pourcentage et les taxes.

Activité préalable

Avoir fait l'exercice de réflexion précédent

Matériel nécessaire

La feuille de travail et une calculatrice.

Déroulement: en une étape

L'animatrice ou l'animateur:

• distribue la feuille de travail;
• explique que les signes indiquant les opérations ne sont pas inscrits et qu'il faut les trouver;
• questionne le sens de chaque donnée inscrite pour établir les relations entre les quantités en cause et déterminer l'opération à effectuer.

Le calcul peut se faire avec la calculatrice ou par écrit si l'on veut pratiquer les algorithmes.

[Voir l'image pleine grandeur]

Voici différentes façons de résoudre les problèmes.

Il faut montrer qu'il existe plusieurs façons de calculer et de quelle manière jouer avec les nombres. Il est plus facile de résoudre un problème en faisant des tableaux ou des listes ordonnées. Les personnes habituées à calculer mentalement utilisent plus facilement ces méthodes.

Présenter le problème sous forme de tableau facilite le calcul:

[Voir l'image pleine grandeur]

À 5 km, on peut doubler la distance et aussi la somme pour avoir:

[Voir l'image pleine grandeur]

Voici un autre problème qui, à première vue, peut paraître difficile. Présenté sous forme de tableau, il devient plus simple.

Quand je parcours 10 km, cela fait environ six milles.

L'Île d'Orléans est à 40 km. Combien cela fait-il de milles aller/retour?

[Voir l'image pleine grandeur]

• Calculer le coût du repas à l'aide des personnages de l'illustration

Dans chaque rangée complète, il y a 10 personnes.

À 10$ en comptant par 10, cela fait	100,00 $
Il y a trois rangées, cela fait	300,00 $
+ 2$ en comptant par 2, cela fait	20,00 $
Il y a trois rangées, cela fait	60,00 $

Et la dernière rangée n'est pas complète mais se calcule de la même façon:

Quatre adultes	40,00 $
	8,00 $
Trois enfants	18,00 $

• Calculer les revenus

Que représentent ces 8$? Combien doit-il y en avoir si les enfants ne paient pas?

C'est dans une situation semblable que l'on découvre le sens et l'importance de la multiplication. On laisse d'abord les gens essayer de résoudre le problème. Certains y arriveront avec des moyens très originaux, mais tous verront l'utilité et l'application de la multiplication, 34 fois 8$.

$8 $8 $8 $8 $8 $8 $8 $8 $8 $8
$8 $8 $8 $8 $8 $8 $8 $8 $8 $8
$8 $8 $8 $8 $8 $8 $8 $8 $8 $8
$8 $8 $8 $8

Pour trouver combien doit débourser le club social, on peut présenter le problème sous cette forme:

Les dépenses s'élèvent à 575$ et les revenus à 272$.

[Voir l'image pleine grandeur]

Durée de l'activité: six heures pour les débutants qui pratiquent les opérations de base. Trois heures pour les plus avancés.

Imprimer l'exercice complet

Notes et commentaires

Une fois qu'elles ont compris quelle opération il faut effectuer, les personnes participantes vont surtout travailler avec la calculatrice. Cet outil leur permet d'effectuer des calculs qu'elles ne pourraient pas faire autrement. Certaines personnes devront recommencer plusieurs fois pour réussir. Les opérations avec les décimales ou le calcul de la taxe sont les plus difficiles. Il est bon de demander aux personnes qui ont plus de difficultés d'expliquer ce qu'elles ont fait et si elles peuvent refaire une autre fois le calcul pour approfondir et fixer l'apprentissage.

On peut aussi demander aux gens plus avancés de pratiquer l'opération par écrit ou de montrer aux autres comment ils ont fait, par exemple, pour calculer la taxe ou comment faire 80 fois 150.

Activité 4 - Évaluation de l'activité

Objectifs

Amener les participantes et participants à développer un esprit critique.
Amener les participantes et participants à évaluer la somme de travail que demande l'organisation d'une activité par rapport au résultat obtenu.

Difficultés que pose l'activité

En général, après une activité, le club social procède à une évaluation. Cela permet de mesurer le degré de satisfaction et de savoir ce que les gens préfèrent. Nous allons utiliser cette situation pour travailler et approfondir les notions de rapport, de proportion et de pourcentage.

Raisonnements impliqués et apprentissages attendus:

• Il existe plusieurs façons de calculer. Toute méthode est bonne. Il suffit de faire des essais, des dessins ou des tableaux, même si parfois la démarche est plus longue.
• Introduction aux notions de pourcentage.

Activités préalables

• Avoir fait l'exercice précédent.
• Posséder des notions de pourcentage.

Matériel nécessaire

• Les résultats effectifs et financiers de la sortie
• Les statistiques du groupe

Déroulement: travail en grand groupe

L'animatrice ou l'animateur:

• revient sur les résultats de la sortie;
• trouve avec les participantes et participants, différentes façons de solutionner les problèmes.

Note: Les questions ou problèmes qui suivent sont uniquement donnés à titre d'exemple pour illustrer comment on peut tirer parti d'une situation et s'en servir comme moyen d'apprentissage et de perfectionnement. Des exemples de résolution des problèmes sont expliqués dans les pages suivantes.

Évaluation de la sortie

Vérifions la participation en cherchant le pourcentage des personnes qui ont participé à la sortie.

• Quel pourcentage représente la présence à l'activité cabane à sucre

1. des participantes et participants,
2. des animatrices,
3. des enfants?

• Quelle fraction du coût du repas représentent les 8$ demandés? Transformer cette fraction en pourcentage.
• Chercher le coût de revient par personne pour l'activité.
• Donner en pourcentage la part que doit débourser le club social. Est-ce qu'on aura le même pourcentage si on fait le calcul pour une personne puis pour l'ensemble des coûts?
• Êtes-vous satisfait de la sortie? À quel pourcentage évaluez-vous le degré de satisfaction par rapport:

1. au prix demandé pour l'activité,
2. à son organisation et à sa réalisation?

L'animatrice ou l'animateur propose différentes démarches.

On compte 72 participantes et participants dans notre groupe; 29 ont participé à l'activité.

Déjà, on peut dire que c'est moins que la moitié des personnes.

[Voir l'image pleine grandeur]

Illustrons la donnée:
dans chaque groupe de sept personnes, il y a trois personnes qui ont participé.

[Voir l'image pleine grandeur]

Autre présentation (méthode utilisée par une personne habile en tables):

[Voir l'image pleine grandeur]

soit environ 42 personnes sur 100 ou 42 pour cent ou 42%. Notre participation aura été d'environ 40%.

Voici une autre méthode utilisée par un participant pour résoudre ce problème.

Quel pourcentage représente la présence des enfants à l'activité cabane à sucre? Il y avait trois enfants sur les 37 personnes.

On arrondit à 3 sur 40, puis on double: 6 sur 80. Il manque 20 pour faire 100. C'est la moitié de 40, donc la moitié de 3, soit 1 et 1/2.

[Voir l'image pleine grandeur]

Lorsqu'on arrive à un résultat qui comporte des fractions, on peut s'attendre à des questions du genre: comment peut-on avoir des demi-personnes? C'est impossible. Ces questions amènent une réflexion sur le sens du pourcentage. Il est difficile pour les gens de saisir qu'il ne s'agit plus de personnes mais seulement de chiffres, et que le pourcentage devient un point de comparaison dont la base est toujours 100.

Durée de l'activité: trois heures

Imprimer l'exercice complet

Commentaires généraux

On peut facilement résoudre des problèmes complexes sans connaître les règles de calcul traditionnelles. Si on ne propose pas ces règles au début, on découvrira que certaines personnes ont développé des moyens très originaux pour calculer. En explorant ces procédés, en encourageant ces initiatives, les essais comme les erreurs, on stimule les gens à trouver leurs propres méthodes. On améliore ainsi leur compréhension et leur confiance en leurs possibilités.

Les personnes qui n'ont pas acquis et mémorisé suffisamment les notions de base en addition et en multiplication éprouvent des difficultés avec ces façons de faire. Souvent, elles s'en tiennent à la calculatrice et n'osent pas explorer d'autres moyens. Il faut leur montrer à quel point il est important de connaître les combinaisons de base et leur fournir des outils pour les mémoriser.

Un projet de cantine

[Voir l'image pleine grandeur]

Un projet de cantine

Le thème de la «cantine» représente une activité globale d'apprentissage en calcul; c'est en outre une activité à moyen ou à long terme, selon l'orientation qu'on veut lui donner. Préparer la cantine et assurer son fonctionnement supposent une volonté commune de concrétiser un projet utile pour la plupart des personnes qui fréquentent le groupe d'alphabétisation. En plus des services qu'elle offre, la cantine peut aussi devenir une source d'autofinancement pour des activités sociales. En ce sens, les participantes et participants guidés par l'animatrice ou l'animateur devront, avant toute chose, définir quels sont les objectifs de leur projet, en plus de ceux liés aux mathématiques.

Dans le but de développer l'expérience mathématique des participantes et participants et d'approfondir les notions apprises, ce projet comporte des activités où l'on retrouve soit l'un soit plusieurs des éléments suivants:

• les opérations de base (addition, soustraction, multiplication, division);
• les nombres décimaux;
• les pourcentages;
• l'argent, la monnaie et le change;
• le prix de revient et la notion de profit;
• les transactions bancaires: livret de caisse, dépôt, chèque;
• le paiement des factures;
• la tenue de livres;
• l'achat et l'inventaire, etc.

Par ailleurs, l'autonomie et la capacité d'évaluation, d'estimation et de négociation constituent autant d'aptitudes qui sont développées tout au long du déroulement des activités. De par son caractère concret et par le sens des responsabilités que ce projet demande, les personnes participantes apprécient beaucoup le travail à réaliser.

La manipulation, on le verra, est un facteur d'apprentissage important. Toutefois, le passage aux exercices écrits et la verbalisation de ce que l'on fait (expliquer oralement sa stratégie de résolution de problème) constituent des éléments tout aussi déterminants dans le processus. Enfin, le degré de difficulté des exercices proposés varie et permet aux personnes de travailler à leur rythme, en fonction de leur niveau propre.

Les activités présentées ici ne s'enchaînent pas les unes après les autres mais se réalisent de façon simultanée. Par exemple, il faut, bien entendu, organiser la tenue de livres dès le début des opérations de la cantine et non pas uniquement à la fin.

Objectif général du thème de la cantine:

Développer et enrichir son expérience mathématique en mettant sur pied une cantine au service des personnes qui fréquentent le groupe d'alphabétisation, et en assurer le fonctionnement.

Activité 1 - La mise en place

Objectifs

Planifier le projet de cantine: évaluer divers scénarios possibles.
Évaluer les ressources disponibles et celles à trouver.
Estimer les meilleurs coûts et trouver les fournisseurs.
Aborder les notions de prix de revient et de profit.

Difficultés que pose l'activité

La mise en place d'une cantine demande un travail de planification important. C'est un exercice d'organisation: comment allons-nous nous y prendre, quels produits voulons-nous vendre, à quel prix, quelles sont nos ressources financières, etc.? Les personnes participantes doivent alors calculer, estimer, évaluer et considérer le projet sous différents angles.

Raisonnements impliqués et apprentissages attendus:

• Se familiariser avec le vocabulaire utilisé.
• Comparer des prix, estimer des quantités.
• Comprendre les taxes.
• Voir les nombres décimaux (monnaie) et l'écriture de l'argent.

Activités préalables

• Avoir travaillé avec de l'argent.
• Avoir travaillé le sens des quatre opérations de base.
• Avoir fait des exercices pour «arrondir».

Matériel nécessaire

• Une liste de prix provenant de deux fournisseurs et un contrat pour la location/achat d'une distributrice (contact avec un représentant)
• Des calculatrices, de l'argent de papier et de la monnaie
• Un tableau des achats (voir plus loin)

Déroulement: les étapes

Première étape, travail en grand groupe

Définir le projet, ce que l'on veut faire.

L'animatrice ou l'animateur:

• demande aux personnes quelles sont les choses à prévoir et de quoi on a besoin pour ouvrir une cantine.

On dresse une liste des éléments qui font l'unanimité, par exemple:

• un local, une table ou un comptoir;
• un réfrigérateur;
• une caisse enregistreuse;
• des produits à vendre (expliquer les termes «approvisionnement» et «fournisseur»);
• des caissiers et caissières (un fonctionnement régulier);
• un montant d'argent de départ ou fonds de démarrage (expliquer le terme «mise de fonds»).

En ce qui concerne le choix des produits à offrir, on peut profiter de l'occasion pour discuter de la pertinence de sensibiliser les gens à une saine alimentation.

On peut décider de démarrer la cantine avec une quantité limitée de produits qui se conservent facilement: des jus, des liqueurs douces, du café, du V-8, de l'eau de source, plusieurs sortes de fruits, des barres tendres, etc.

Pour l'organisation matérielle, l'animatrice ou l'animateur aide les participantes et participants à:

• trouver et aménager un espace;
• trouver un ou deux réfrigérateurs;
• trouver une caisse enregistreuse;
• trouver un fonds de démarrage: évaluer les besoins, ce qu'il faut acheter avant de démarrer les opérations de la cantine; on peut demander au groupe d'alphabétisation de prêter la somme nécessaire, par exemple 200$, et prévoir les modalités de remboursement;
• se donner un fonctionnement régulier et des règles:

- prévoir un fonctionnement souple qui permet à tous de participer,
- former des équipes de travail,
- définir un horaire d'ouverture (pauses, repas),
- définir quelques règlements de base concernant le crédit, la responsabilité des caissiers et caissières, la fréquence de l'inventaire, du calcul de la caisse, des dépôts à faire, etc.

Deuxième étape, en grand groupe

L'approvisionnement (recherche des meilleurs prix)

L'animatrice ou l'animateur:

• à partir de listes provenant de fournisseurs (ou de factures), propose de comparer les prix de divers articles pour trouver les plus intéressants.

Note: on peut aussi aller visiter certaines épiceries pour recueillir et comparer les prix.

L'animatrice ou l'animateur remet à chaque personne une feuille sur laquelle sont présentés, sur deux colonnes parallèles, les prix d'achat des produits que l'on veut offrir à la cantine. Ici, on en profite pour arrondir.

Liste des prix

Produits	Fournisseur X	Fournisseur Y
Barres tendres	8/1,85$ tx inc.	8/1,69$ tx inc.
Pommes	2lb/1,39$	5lb/3,98$
Jus V-8 250ml	12/4,79$	6/2,59$

L'animatrice ou l'animateur:

• demande si, pour un même produit, la quantité est égale;
• demande d'identifier les articles qui sont taxés;
• demande de trouver, pour chaque produit, le prix le plus bas.

Exemple:

Une boîte de huit barres tendres coûte 1,85$ chez Métro et 1,69$ chez Héritage (remarquer que le produit est taxable). Quelle est la moins chère? Les moins avancés peuvent illustrer le problème avec de l'argent et trouver combien ajouter pour obtenir le même montant:

1$ + 25¢ + 25¢ + 25¢ + 10¢
1$ + 25¢ + 25¢ + 10¢ + 5¢ + 1¢ + 1¢ + 1¢ + 1¢

La différence est de 16¢.

Quelle opération mathématique peut-on faire pour trouver la différence entre deux prix? Une soustraction. Vérifier.

Nous retrouvons ici le troisième sens de la soustraction, à savoir un sens de comparaison (voir le chapitre sur la soustraction). Il faut profiter de l'occasion pour mieux définir ce sens. Dans le cas présent, on peut facilement découvrir la différence sans soustraire. Cependant, on peut faire remarquer que parfois, il est plus facile d'utiliser la soustraction. Donner des exemples avec des nombres plus grands.

Les personnes choisissent ensuite, selon les meilleurs prix, le ou les fournisseur(s) où acheter les produits.

Il est possible d'introduire ici les taxes (voir le tableau à la fin).

Une fois qu'on a choisi les fournisseurs pour une partie des articles offerts par la cantine, l'animatrice ou l'animateur soulève la question de l'approvisionnement en liqueurs douces: est-il préférable de signer un contrat avec un représentant (achat ou location d'une distributrice) ou d'avoir notre propre réseau de vente?

L'animatrice ou l'animateur:

• propose de rencontrer un représentant de distributrices à liqueurs douces pour savoir s'il est plus rentable de s'approvisionner soi-même ou de louer (ou acheter) une distributrice.

Le groupe rencontre le représentant qui explique les conditions du contrat de location ou d'achat. Une personne du groupe peut se charger d'établir le contact avec le représentant

Le groupe discute, évalue et compare les différents scénarios:
Dans le cas d'un contrat de distributrice:

• le contrat prévoit laisser à la cantine 250 par liqueur, plus 50 par cannette vide;
• la liqueur se vend 1$;
• le choix est limité;
• le distributeur s'occupe de tout.

Dans la situation actuelle, par exemple le cas du groupe (club social):

• la liqueur se vend 50¢;
• le choix est plus grand;
• le club social (ou la cantine) s'occupe de tout.

Pour connaître le pourcentage de profit sur chaque liqueur, il faut connaître le prix d'une liqueur.

Nous payons 13$ pour deux caisses de 24 liqueurs. Comment fait-on pour trouver le prix d'une bouteille? Il faut séparer. Nous retrouvons un problème de division de partage qui est difficile à expliquer: diviser l'argent entre les 48 bouteilles.

On laisse les gens essayer sans calculatrice. Certaines personnes réussiront par divisions successives par 2 et 3:

une caisse de 24 pour 6,50$, 12 pour 3,25$, 6 pour 1,60$ environ, 2 pour 50¢, soit 25¢ la bouteille, ce qui est proche du prix réel à 27¢.

On peut essayer par tâtonnement:

48 liqueurs	À 1$ ça fait	48$ c'est trop
48 liqueurs	À 50¢ c'est la moitié	24$ c'est trop
48 liqueurs	À 25¢ c'est la moitié	12$ c'est proche

Les personnes vérifient le calcul avec la calculatrice.

Cherchons le pourcentage de profit

La distributrice: 25¢ + 5¢ pour la cannette, soit 30¢ pour chaque 1$ de vente.
Ce qui veut dire 30¢ sur 100¢ ou 30%

Notre réseau: 50¢ - 27¢ = 23¢ de profit, soit 23 sur 50 x 100
ou plus simplement: 23¢ + 23¢ = 46¢ pour chaque $1 de vente ou 46%

Enfin, les participantes et participants doivent décider qui ira acheter les produits. Les personnes choisies devront inscrire les achats sur un «tableau des achats» qui servira plus tard à faire l'inventaire.

Exemple de tableau des achats

Produits	Sept	Sept	Oct.	Date	Date	Date	date
	9	23	2
Seven Up	12	12
Pepsi	24
Jus d'orange	24	12
V8 (250 ml)	12	24
V8 (340 ml)	24	18
Tisanes	15
Lait au chocolat	12	12

Durée de l'activité: cinq heures

Imprimer l'exercice complet

Notes et commentaires

Il faut prendre le temps de bien montrer le sens des opérations à effectuer pour calculer le prix de revient (la division) et le profit (la soustraction), de manière à ce que les participantes et participants comprennent l'utilité de chacune.

Par ailleurs, en ce qui concerne l'écriture de l'argent, le rôle de la virgule ou du point et la place du zéro, on peut prévoir quelques exercices écrits pour pratiquer l'addition de montants d'argent. Ces activités permettent aux participantes et participants de développer leur capacité d'estimer et de comparer: ce produit est plus cher que..., moins cher que...

Il ne faut pas oublier de compléter le tableau des achats à chaque fois que l'on achète des produits, de manière à cumuler sur une même feuille le total des achats réalisés pendant la période de fonctionnement de la cantine. Cet instrument sera nécessaire au moment de l'inventaire.

Activité 2 - Trouver le prix de revient et fixer le prix de vente des produits

Objectifs

Lire et vérifier les factures (comprendre les taxes).
Déterminer le prix à l'unité - prix de revient (travailler la division et la multiplication).
Fixer les prix de vente (travailler la soustraction).
Sensibiliser les participantes et participants à la notion de profit.
Pratiquer l'écriture des montants d'argent.

Difficultés que pose l'activité

On va retrouver dans cette activité les quatre opérations de base. Il faut donc bien distinguer le sens de chacune pour arriver à fixer le prix de vente des produits à la cantine.

Raisonnement impliqués et apprentissages attendus:

• Lire et écrire les montants d'argent.
• Comprendre le sens des opérations.
• Apprendre à se servir de la calculatrice.

Activités préalables

• Avoir travaillé avec de l'argent.
• Avoir travaillé le sens des quatre opérations de base.
• Avoir acheté les produits que l'on veut offrir à la cantine.

Matériel nécessaire

• Les factures des achats réalisés pour la cantine
• Les listes des produits achetés (avec les quantités)
• Des calculatrices

Déroulement: les étapes

Première étape, travail en grand groupe

Calcul du prix de revient

L'animatrice ou l'animateur:

• remet aux participantes et participants une copie des factures d'achat: ensemble, on en fait la lecture;
• fait identifier les produits qui sont taxés (au besoin, reprendre le tableau des taxes);
• pour chacun des articles inscrits sur la facture, demande comment on peut en déterminer le prix à l'unité.

Exemple:

Comment calculer le prix d'une cannette de Coke si 12 cannettes coûtent 4,61$?

L'animatrice ou l'animateur travaille avec les personnes. On illustre l'opération:

[Voir l'image pleine grandeur]

À retenir, pour trouver le prix à l'unité: je dois diviser le prix total par le nombre d'objets.

Les personnes travaillent avec la calculatrice. On fait remarquer la place du point (équivalent de la virgule) et l'écriture de la monnaie. On reprend ce travail pour chacun des produits achetés en précisant les articles qui sont taxables (les plus avancés calculent les taxes).

Les personnes écrivent le prix total et le prix à l'unité sur un tableau semblable.

Produits (Quantité)		Taxe	Prix	Total	Prix / unité
12 Coke			4,61		0,38
12 Orange Crush			4,9
36 liqueurs Zel			9,32
3 Jus Pomme			0,99
12 Jus V8 350 ml			7,2

Deuxième étape, en grand groupe

Prix de vente et calcul du profit

L'animatrice ou l'animateur:

• demande aux participantes et participants de fixer le prix de vente de ces mêmes articles;
• laisse discuter les personnes;
• demande comment on doit faire pour calculer le profit que la cantine va faire sur chaque produit vendu (expliquer la notion de profit).

Pour trouver le profit, on a besoin de savoir:

• le prix d'achat à l'unité et le prix de vente;
• la différence entre ces deux prix, c'est le profit.

À retenir: le profit, c'est le prix de vente moins le prix d'achat.

Pour une cannette de coke:

[Voir l'image pleine grandeur]

Illustrer la soustraction avec de la monnaie.

Reprendre la liste des produits en inscrivant le prix de vente et le profit.
Par la suite, les personnes vont étiqueter le prix de vente des produits.

Liste des produits achetés: profit

Produits (Quantité)	Prix d'achat/unité	Prix de vente/unité	Profit/unité
12 Coke	0,38	0,75	0,37
12 Orange Crush	0,41
36 liqueurs Zel	0,26
3 Jus Orange	0,33
12 Jus V8 350 ml	0,6

Durée de l'activité:quatre heure

Notes et commentaires

En manipulant les emballages de trois jus, on peut apprendre la table de 3:
1 groupe de 3 = 3; 2 groupes de 3 = 6, etc.

De même, on verra la table de 12 en calculant le profit des barres tendres:
1 barre = 1 x 12¢, 2 barres = 2 x 12¢, etc., puis par écrit:

[Voir l'image pleine grandeur]

Avec 24 jus pour 8,00$, on fera la division:

12 jus pour 4,00$
6 jus pour 2,00$
3 jus pour 1,00$
1 jus pour ?

On trouve la réponse par essai/erreur:
à 25¢: 25 + 25 + 25, ce n'est pas assez
à 50¢: 50 + 50 + 50, c'est trop
à 30¢:30+ 30+ 30, pas encore assez
On ajuste à 33¢:33 + 33 +33

Cette activité permet de travailler les quatre opérations. De façon générale, les personnes apprécient ce travail en raison de son caractère concret.

Il faut également ajuster les exercices en fonction du degré de connaissance des personnes formant les groupes. Certaines pourront travailler les taxes ou les pourcentages de profit pendant que d'autres travailleront par exemple l'addition ou l'écriture des nombres.

Imprimer l'exercice complet

Activité 3 - La caisse

Objectifs

Lire et écrire les montants d'argent (nombres décimaux).
Savoir calculer et rendre la monnaie (soustraction au sens d'addition de complément).
Apprendre le fonctionnement de la caisse enregistreuse.
Calculer le total de la caisse.

Difficultés que pose l'activité

L'addition, la soustraction et la multiplication sont des opérations nécessaires quand on calcule la caisse. Les participantes et participants doivent compter par 5, 10, 25 et par 2 pour calculer le total de l'argent En rendant la monnaie, ils doivent aussi calculer mentalement. L'écriture et la lecture des montants sur la caisse enregistreuse nécessitent une compréhension des nombres décimaux.

Raisonnements impliqués et apprentissages attendus:

• Écrire correctement les montants d'argent (place de la virgule ou du point et du zéro).
• Compter par 2, 5, 10, 25.
• Faire des regroupements pour faciliter le calcul.

Activités préalables

• Avoir travaillé avec de l'argent.
• Avoir suivi les activités précédentes.

Matériel nécessaire

• Une caisse enregistreuse
• De l'argent de papier (billets) et de la monnaie
• Quelques produits à vendre
• Des bordereaux de dépôt
• Des calculatrices

Déroulement: les étapes

Première étape, travail en grand groupe

Simulation de l'ouverture de la cantine

L'animatrice ou l'animateur:

• demande aux personnes de calculer l'argent déposé comme fonds de caisse dans la caisse enregistreuse (expliquer l'expression «fonds de caisse»);
• demande aux participantes et participants de se diviser en deux groupes: celui des clients et celui des vendeurs-caissiers.

Les gens apprennent à travailler sur la caisse enregistreuse. On fera une rotation des équipes pour que tout le monde puisse travailler à la caisse.

Deuxième étape

Calcul de la caisse

L'animatrice ou l'animateur:

• remet aux personnes du groupe un bordereau de dépôt en expliquant à quoi il sert et comment le remplir;
• demande de calculer l'argent qu'il y a dans la caisse enregistreuse;
• demande de laisser le fonds de caisse;
• observe la façon de calculer.

De plus, on fera remarquer certains regroupements, par exemple:

10 fois 5¢ = 0,50$
20 fois 5¢ = 1,00$ (place de la virgule et zéros)
40 fois 5¢ = 2,00$, c'est un rouleau de 5¢

5 x10¢ = 0,50$
10 x10¢ = 1,00$
50 X10¢ = 5,00$, c'est un rouleau de 10¢

2x25¢ = 0,50$
4x25¢ = 1,00$,
40 X 25¢ =10,00$, c'est un rouleau de 25¢

Durée de l'activité: trois heures

Notes et commentaires

Cet exercice sera repris régulièrement au cours du fonctionnement de la cantine.
Il faut bien faire remarquer l'importance de la virgule et du zéro dans l'écriture de l'argent.
Cependant, il faut que l'animatrice ou l'animateur fasse preuve de souplesse si les personnes utilisent le point au lieu de la virgule dans l'écriture de l'argent.
Sur la caisse enregistreuse, on montre la différence entre 1,00 et 0,01, entre 3,50 et 0,35, etc.

Souvent aussi, les personnes ont de la difficulté à bien aligner les chiffres dans l'addition faite sur papier. Faire des exercices écrits pour pratiquer l'écriture des montants d'argent et l'alignement de chiffres.

Avec le calcul de l'argent de la caisse, certaines personnes ont pu voir très concrètement à quel point il était important de connaître les tables et elles ont appliqué des règles déjà apprises.

• La table de 5, nécessaire pour compter les 5¢.
• La table de 4, pour compter les 25¢ empilés par 4.
• La table de 10, pour le calcul de 10¢.

Cette activité est très appréciée par les participantes et participants qui font fonctionner la caisse, calculent la monnaie, etc.

Fiche 1 – Bordereau de dépôt

[Voir l'image pleine grandeur]

Imprimer l'exercice complet

Activité 4 - L'inventaire (régulier et final)

Objectifs

Faire l'inventaire de la cantine (régulier et final).
Approfondir le sens et la technique de la soustraction.
S'exercer à la multiplication de nombres décimaux.
Se familiariser avec la notion de vente.

Difficultés que pose l'activité

Pour faire l'inventaire, il faut calculer combien d'articles on a vendus par rapport à la quantité totale à l'achat; il faut donc savoir combien il en reste en procédant à la soustraction, avec et sans retenue.

Pour savoir ce que rapporte la vente des produits, on doit multiplier des nombres décimaux (montants d'argent) et des quantités. La lecture et l'écriture de ces nombres sont donc ici essentielles.

Raisonnements impliqués et apprentissages attendus:

• Lire et écrire les nombres décimaux.
• Faire des regroupements.
• Comprendre le sens et les techniques de l'addition, de la soustraction et de la multiplication.

Activités préalables

• Reconnaître le sens des opérations.
• Avoir fait les activités précédentes.
• Avoir fait fonctionner la cantine pendant un certain temps.

Matériel nécessaire

• Des calculatrices
• Des feuilles d'inventaire et de calcul des ventes
• Le tableau des achats

Déroulement: les étapes

Première étape, travail en grand groupe

Compter ce qui reste, inventaire régulier

L'animatrice ou l'animateur:

• distribue les feuilles d'inventaire aux participantes et participants;
• explique le mot «inventaire»;
• demande combien la cantine a vendu d'articles de chaque produit pendant la période déterminée.

Pour chaque item, les personnes du groupe vont compter sur place quelle est la quantité restante.

Ensuite, elles vont compléter la feuille d'inventaire, en calculant la quantité vendue. Il ne faut pas hésiter à illustrer l'opération avec les articles si cela s'avère nécessaire.

Les personnes effectuent la soustraction (sens de complément) sur papier. Celles qui ont des difficultés peuvent utiliser des dessins ou la calculatrice.

Inventaire du (date):

Produits	J'avais	Il reste	Vente
Coke	10	0	10
Seven Up	12	4
Pepsi	24	9

Deuxième étape, en grand groupe

Calculer le montant des ventes

L'animatrice ou l'animateur:

• demande ensuite aux personnes du groupe de calculer combien a rapporté la vente (de la semaine par exemple).

On travaille d'abord avec l'argent.
On prend l'exemple des trois cannettes de coke vendues: on place 3 x 250 devant chaque cannette.
On compte l'argent en le regroupant de diverses façons:

[Voir l'image pleine grandeur]

On recommence l'opération sur la calculatrice:

3 x 0,75, ce qui permet d'apprendre à écrire et lire les montants d'argent.
On poursuit l'exercice pour chaque item, en travaillant si possible avec l'argent et le produit

Les personnes du groupe inscrivent, au fur et à mesure de la démarche, les items sur la feuille «vente totale» que l'animatrice ou l'animateur leur a remise.

Les personnes plus avancées vont calculer sur la calculatrice ou à la main le total des ventes.

Il faut apprendre à bien disposer les chiffres dans l'addition avec des virgules ou des points.

Vente totale pour (date)

Produits	Vente	Prix	Total
V8	8	0,60 $
Jus	35	0,50 $
Etc.

Troisième étape, en grand groupe

L'inventaire final ou bilan

Cet exercice se fait à la fermeture de la cantine.
La démarche se fera en équipe, en utilisant ou non la calculatrice selon les personnes.
L'animatrice ou l'animateur guide le travail.

L'animatrice ou l'animateur:

• distribue le tableau des achats (voir tableau des achats dans l'activité 1) avec lequel une première équipe va travailler, ainsi que des feuilles d'inventaire;
• demande aux personnes de faire le travail suivant:

1. Calculer le total des achats pour chaque produit (l'addition).
2. Faire l'inventaire de ce qui reste (dénombrement).
3. Pour chaque produit, calculer combien d'articles ont été vendus et comparer les résultats: quel produit s'est le mieux vendu? le moins vendu?, etc.
4. Pour les personnes plus avancées, calculer le total de ventes réalisées (multiplication avec décimales).
5. Calculer la valeur des cannettes vides que l'on a en main.

Durée de l'activité: inventaire régulier et calcul des ventes (première et deuxième étape): selon le groupe, environ trois heures.
Inventaire final: variable selon la quantité des produits et les possibilités des partiel pantes et participants.

Imprimer l'exercice complet

Notes et commentaires

Le travail sur l'inventaire constitue une pratique intéressante des opérations de base. Les diverses possibilités d'exercices favorisent un apprentissage global des opérations mathématiques. L'une des difficultés qui revient souvent réside dans l'écriture des montants d'argent (place de la virgule). À cet effet, la caisse enregistreuse constitue un instrument pertinent De plus, on rappellera les signes de chacune des opérations.

À partir de la technique de l'addition, on peut travailler la technique et le sens de la multiplication. Pour la division, les personnes moins avancées ont travaillé avec la calculatrice. Il faut revenir sur la technique du calcul à l'unité.

Activité 5 - Les transactions bancaires Les pourcentages

Cette activité devrait être réalisée avec des groupes
de personnes plus avancées dans leur cheminement.

Objectifs

Se familiariser avec les opérations comptables: tenue de livres.
Se familiariser avec le carnet de caisse.
Apprendre les pourcentages.
Approfondir les techniques des opérations de base.

Difficultés que pose l'activité

Pour effectuer les transactions bancaires, il faut comprendre le sens des opérations (addition et soustraction) et maîtriser l'écriture des nombres décimaux. De la même façon que pour le calcul des pourcentages, cet exercice fait appel à la capacité d'abstraction des participantes et participants. De plus, ces derniers doivent lire les factures et écrire les entrées sur les feuilles comptables.

Raisonnements impliqués et apprentissages attendus:

• Comprendre le vocabulaire utilisé (revenus, dépenses, solde).
• Comprendre le sens des nombres négatifs.
• Connaître les notions de profit et de perte.
• Lire les factures.
• Maîtriser l'addition, la soustraction, la lecture et l'écriture des nombres.

Activités préalables

Avoir suivi les activités précédentes.

Matériel nécessaire

• Des feuilles de revenus et dépenses (feuilles comptables)
• Les factures d'achat
• Les bordereaux de dépôt
• Des feuilles de bilan
• Des calculatrices
• Des photocopies de pages du carnet de caisse de la cantine dont la dernière montrant la charte des codes employés

Déroulement: les étapes

Première étape, en équipe

La tenue de livres

L'animatrice ou l'animateur:

• présente la feuille comptable des revenus et dépenses et explique comment la remplir;
• explique les termes: revenus, dépenses et solde;
• demande aux personnes du groupe d'inscrire les revenus, les dépenses et le solde, en précisant les dates.

Exemple:

Date	Détails	Revenus	Dépenses	Solde
12-02-94	Dépôt	54,5		54,5
17-02-94	Achats fruits		34,25	20,25

Les équipes de travail font les entrées sur la feuille comptable et effectuent les opérations. L'animatrice ou l'animateur rencontre les équipes et les aide. L'écriture sur les feuilles comptables doit se faire régulièrement, selon un rythme défini au départ.

Remarque: Dans le cas où le groupe a emprunté une mise de fonds, il faudra en faire la première entrée sur la feuille comptable. L'animatrice ou l'animateur doit expliquer l'importance de cet élément.

Deuxième étape, en grand groupe

Lecture du carnet de caisse

L'animatrice ou l'animateur:

• présente aux participantes et participants les copies de quelques pages du carnet de caisse;
• engage une discussion: qu'est-ce qui est écrit, que signifient les codes employés?, etc.

Ensemble, on fait l'analyse du carnet de manière à décoder ce qui est inscrit. Il faut prendre le temps de répondre aux questions posées par les participantes et participants.

Troisième étape, en grand groupe

Faire le bilan de l'année

L'animatrice ou l'animateur:

• présente la feuille de bilan et explique les termes non connus: bilan, comptes à recevoir, actif, passif.

À partir des données recueillies au cours du fonctionnement de la cantine, on complète la feuille et on explique les résultats. Après l'analyse de la situation financière, les gens proposent des suggestions pour améliorer le fonctionnement de la cantine pour l'an prochain.

Durée de l'activité: transactions bancaires (première et deuxième étapes): trois heures.
Bilan: trois heures.

Notes et commentaires

À un moment donné, quelqu'un avait suggéré l'idée d'installer une distributrice parce que la vente des liqueurs était déficitaire. La personne qui s'occupait de comptabiliser les entrées avait signalé le fait. Durant l'atelier, nous avons d'abord étudié les livres et la cause du déficit (contrôle insuffisant et liqueurs gratuites non comptabilisées). À partir des chiffres, nous avons pu expliquer pourquoi et comment inscrire les entrées et les sorties d'argent Par la suite, nous avons continué l'analyse des livres comptables du club social et du carnet de caisse. Du fait du caractère concret de ce travail et du sens des responsabilités qu'il demandait, les participantes et participants étaient bien préparés à entreprendre la comptabilité de la cantine.

Même s'il n'y avait qu'un groupe responsable, ce sont toutes les participantes et participants qui ont profité de l'expérience, en ce sens que plusieurs notions ont été introduites à partir de situations rattachées à la cantine. Enfin, on peut dire que l'inventaire de fermeture a servi de test pour évaluer les habiletés que les gens avaient développées durant l'année.

Fiche 2 – Bilan de la cantine

[Voir l'image pleine grandeur]

Quatrième étape

Les pourcentages

Il s'agit ici d'une activité d'approfondissement que l'on peut faire à un moment ou à un autre pendant le déroulement du projet de cantine.

La cantine et le pourcentage

l) J'ai acheté des jus de fruits pour la cantine. Si j'avais acheté 100 jus de fruits, j'aurais les pourcentages indiqués dans le tableau.

Je n'ai pas acheté 100 jus, mais les proportions sont les mêmes.

• Peux-tu trouver combien de jus de chaque sorte j'ai achetés?

[Voir l'image pleine grandeur]

Note: Cet exercice fait appel à la compréhension de la notion de pourcentage et à la règle de trois. Les premiers cas sont plus faciles alors que les derniers exigent une application de la règle:

[Voir l'image pleine grandeur]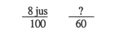

De plus, comme il est impossible d'acheter une fraction de jus, il faut compléter ou non selon la fraction.

2) Les achats du 25/04/94

Hier, j'ai acheté 75 fruits de différentes sortes indiquées dans le tableau.

• Transforme ces quantités en pourcentage.
• Ensuite, cherche le prix à l'unité.

[Voir l'image pleine grandeur]

Les fruits sont vendus 25¢/pièce.

Nous avons dû jeter trois fruits.

• Quel est le pourcentage de profit sur l'ensemble des fruits?

Exercices complémentaires (travail individuel)

La cantine et les 4 opérations
Les + , les - , les x , les ÷:

Sépare la caisse de 12 liqueurs

Le travail se fait d'abord avec les caisses de liqueurs, puis on l'exprime en nombres sur une feuille.

Sépare en 2, 3, 4, 6.

[Voir l'image pleine grandeur]

Les personnes séparent chaque caisse et font l'opération mathématique (division). Dans chaque cas, on peut procéder de deux façons. Par exemple, en séparant en deux: faire deux groupes de six ou six groupes de deux; ou en séparant en trois ou faire des groupes de trois; faire trois groupes de quatre ou quatre groupes de trois, etc.

Cherche le prix à l'unité

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

Fais les soustractions

[Voir l'image pleine grandeur]

Complète le tableau (taxes)

[Voir l'image pleine grandeur]

L'animatrice ou l'animateur explique le tableau.
Ensemble, on le complète en estimant d'abord, puis en vérifiant avec la calculatrice.

Imprimer l'exercice complet

Les semences

[Voir l'image pleine grandeur]

Les semences

Le thème des «semences» vise à approfondir les connaissances mathématiques des participantes et participants dans le cadre d'une activité concrète qui, au moment de l'expérience, a été beaucoup appréciée par les membres du groupe.

En préparant des semis pour le jardin, les personnes travaillent avec des regroupements et se familiarisent principalement avec la multiplication dans son sens d'aire ou de configuration rectangulaire. Mais les exercices exigent que l'on ait aussi recours aux autres opérations; par exemple, quand viendra le temps de planter les graines dans les caissettes de semis, on reverra la notion de division.

Le degré de difficulté des activités proposées varie. Il est donc possible d'aborder ce thème avec un groupe hétérogène, car il offre différents exercices correspondant aux divers niveaux des participantes et participants.

La démarche suggérée repose sur une grande part de manipulation. Ces moments sont importants parce qu'ils permettent aux personnes de visualiser et ainsi de mieux comprendre les mécanismes mathématiques en jeu, et à l'animatrice ou l'animateur de mieux comprendre la façon de travailler des personnes du groupe et leurs stratégies de résolution de problèmes.

On peut commencer à travailler «les semences» au début du mois de février et poursuivre ce processus d'apprentissage tout au cours du printemps. On verra pousser les plants de semaine en semaine.

Lorsque ceux-ci arriveront à maturité, il sera possible d'organiser une vente de plants, ce qui permettra de calculer le prix de revient de la production et, par conséquent, de pratiquer les diverses opérations mathématiques requises (addition, soustraction, etc.). Différents apprentissages sont réalisables comme on le verra plus loin. De plus, on peut faire de cette vente une activité bénéfice dans le but d'amasser des fonds pour le groupe.

Plutôt qu'une vente, on peut aussi choisir de semer les plants dans un jardin, ce qui amènera les participantes et participants à calculer les surfaces et à travailler la question des échelles, des rapports et des proportions. C'est la démarche que nous avons expérimentée.

Dès le début de ce thème, l'animatrice ou l'animateur veillera à expliquer les différentes étapes de la démarche proposée.

Objectif général de ce thème:

En partant des semis pour le jardin, apprendre la multiplication dans son sens d'aire ou de surface, et pratiquer les opérations mathématiques de base.

Activité 1 - Présentation du thème et exploration du matériel

Objectif

Par manipulation, explorer les combinaisons possibles de divers groupements.

Difficultés que pose l'activité

Les personnes participantes sont plus familières avec la multiplication dans son sens d'addition répétée. Les exercices qui suivent sont davantage axés sur l'autre sens de cette opération, celui d'aire ou de surface. En manipulant des caissettes de six plants, les personnes forment des groupes et des nombres qu'il faut combiner avec d'autres et doivent recourir à leur capacité d'abstraction et de calcul mental.

Raisonnements impliqués et apprentissages attendus:

• Travailler par regroupements.
• Compter par 2, par 3, par 4, par 6.

Activités préalables

• Avoir auparavant travaillé à partir de regroupements d'objets et de nombres.
• Savoir associer l'ensemble au nombre d'éléments qu'il contient.

Matériel nécessaire

Plusieurs caissettes de semis de six plants (2 x 3 plants):

[Voir l'image pleine grandeur]

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• place les caissettes sur la table;
• invite les personnes à manipuler les caissettes et à les disposer comme elles l'entendent (collées, séparées): faire des groupes de 6, de 12, de 24, de 48;
• laisse compter et discuter selon les dispositions réalisées: par exemple, dans un contenant, 3 rangées de 2 font 6 ou 2 rangées de 3 font 6.
• demande aux personnes de commenter les modifications causées par les changements de dispositions qu'elles opèrent: par exemple,

2 groupes de 6, ça fait 12;
reprendre:
2 groupes de 6 ou 2 fois 6, ça fait 12;
2 groupes de 12 ou 2 fois 12, ça fait 24;

• demande si on peut faire 12 d'une autre façon qu'avec 2 groupes de 6, en plaçant (ou collant) les caissettes autrement: ainsi,

6 groupes de 2 (ou 6 fois 2) ou
3 groupes de 4 (ou 3 fois 4) ou
4 groupes de 3 (ou 4 fois 3)

• propose de faire la même chose avec le 24, en collant quatre caissettes:

- placés bout à bout ( rangées de 12 et de 2);

- placés côte à côte ( rangées de 8 et de 3);

- en rangées de 6 et de 4.

Deuxième étape

L'animatrice ou l'animateur:

• tout en demandant au groupe de déplacer les caissettes pour les disposer bout à bout, introduit la table de 2;
• des exercices écrits sont alors intégrés; on peut reproduire au tableau les caissettes et écrire les équations mathématiques correspondantes:

[Voir l'image pleine grandeur]

Troisième étape

Cet exercice de manipulation permet aussi d'aborder la notion de division, toujours en se servant des caissettes de semis placés de diverses façons.

L'animatrice ou l'animateur demande alors aux personnes du groupe, par exemple:

• Combien de rangées de 6 dans 12?
• Combien de groupes de 2 dans 12?
• Combien de rangées de 4 dans 12?
• Combien de groupes de 12, de 4, de 6, de 8 dans 24?

Durée de l'activité: une heure trente

Imprimer l'exercice complet

Notes et commentaires

Il faut toujours parler en termes de «rangées» ou de «groupes»:

• 2 rangées de 12 ou 2 fois 12 caissettes;
• 12 rangées de 2 ou 12 fois 2 caissettes;
• 4 rangées de 6 ou 4 fois 6 caissettes;
• 8 rangées de 3 ou 8 fois 3 caissettes.

Aussi, comme le 24 fait penser à la caisse de 24, on peut demander de placer les caissettes de la même façon.

Cette activité montre une autre facette de la multiplication ou une autre utilité à cette opération mathématique.

En général, les personnes ont compris. Pour ceux et celles qui ont eu des difficultés à visualiser les opérations ou les groupements qu'il fallait faire, il a été utile de découper en 3 les caissettes de 6 plants de manière à former des groupes de 2.

Activité 2 - La table de multiplication de 2 et de 3

Objectifs

Donner un sens à la multiplication.
Permettre aux personnes de s'exercer avec les tables de 2 et de 3.

Note: selon le degré d'avancement des personnes du groupe, on peut aborder ici les tables de 4, 5 et 6.

Difficultés que pose l'activité

Le passage de l'addition répétée à la multiplication prise dans son sens d'aire ou de surface.

Raisonnements impliqués et apprentissages attendus:

• Travailler par regroupements.
• Compter par 2, par 3 (par 4 ou par 5).

Activités préalables

Avoir travaillé avec les caissettes et avec des regroupements.

Matériel nécessaire

• Des caissettes de semis pour six plants
• Des gobelets à l'unité (genre contenant de crème à café ou à médicament)
• Des feuilles de pratique (voir ci-après)

Déroulement: les étapes

Travail en grand groupe.

Première étape: les multiples de 2 (révision)

L'animatrice ou l'animateur:

• dépose sur la table les gobelets et les caissettes de six plants;
• demande aux personnes d'illustrer avec ces objets la table de 2 soit:

[Voir l'image pleine grandeur]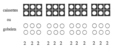

Nous avons utilisé les gobelets, car certaines personnes avaient de la difficulté à isoler le «deux» dans les caissettes de semis. Il ne s'agit plus alors d'aire. Il faut, une fois que la personne a compris, revenir à la notion d'aire à l'aide des caissettes.

On reprend ensemble en comptant par 2.

1 groupe de 2 =2
2 groupes de 2 = 4
3 groupes de 2 = 6, etc.

Puis les personnes complètent la feuille de la table de 2 (à partir des gobelets pour celles moins avancées).

Il est également possible d'écrire la division correspondante à côté:

1 x 2 = 2
2 x 2 = 4, 4 ÷ 2 = 2
2 x 3 = 6, 6 ÷ 2 = 3 etc.

Deuxième étape: les multiples de 3

L'animatrice ou l'animateur:

• reprend les gobelets et les caissettes de six plants et demande aux personnes de les disposer par groupes (rangées) de trois:

[Voir l'image pleine grandeur]

On reprend ensemble en comptant par 3:

1 groupe de 3 = 3
2 groupes de 3 = 6
3 groupes de 3 = 9, etc.

Les personnes complètent la feuille de la table de 3 (à partir de gobelets pour les moins avancées).

Durée de l'activité: deux heures

Notes et commentaires

Généralement, la table de 2 ne cause pas trop de problèmes.

On peut aussi développer davantage l'exercice en introduisant, de la même façon, les tables de 4, de 5 ou encore de 6.

Par l'utilisation des gobelets et des caissettes de semis de six plants, il est possible de se familiariser, en même temps, avec les deux sens de la multiplication: en manipulant les gobelets, c'est l'addition répétée; en manipulant les caissettes, c'est l'aire ou la surface qui est considérée.

Feuille de pratique des tables 2 et 3

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

[Voir l'image pleine grandeur]

On retrouve ici la multiplication verticale. De plus, on touche à la multiplication avec des nombres plus grands que 10. On fait observer comment la multiplication peut se décomposer. On peut se reporter au chapitre sur la multiplication et reprendre l'exercice avec les verres et les cartons si les gens rencontrent des difficultés.

Imprimer l'exercice complet

Activité 3 - Les semences

Objectifs

Approfondir le sens de l'addition par groupements, de la multiplication (sens d'aire ou de surface) et de la division. Chacune des six cases des caissettes représente une unité d'aire. Préparer les semis.

Difficultés que pose l'activité

En préparant les semis, les personnes doivent calculer le nombre de graines en rapport avec le nombre de caissettes et de gobelets qu'ils ont. C'est encore la notion d'aire ou de surface qui est développée, mais on aborde aussi la notion de répartition (division).

Raisonnements impliqués et apprentissages attendus:

• Le calcul par regroupements est plus rapide.
• La multiplication (sens d'aire ou de surface).
• La répartition par caissettes ou la division.

Activités préalables

• Avoir travaillé avec les caissettes et les gobelets.
• Avoir travaillé avec des regroupements.
• Savoir associer l'ensemble au nombre d'éléments qu'il contient.

Matériel nécessaire

• Des caissettes de semis à six cases
• Des pots de semences à l'unité
• Du terreau ou de la terre à jardin
• Des semences (graines de plantes, de fleurs, de fines herbes, etc.)

Le déroulement: les étapes

Première étape: travail de manipulation avec les semences en grand groupe

L'animatrice ou l'animateur:

• dépose sur la table des graines et des pots;
• donne la consigne de disposer les pots en rangées; chaque personne doit déposer un nombre de graines par pot, deux, trois, quatre ou cinq graines par exemple:

[Voir l'image pleine grandeur]

On reprend ensemble en calculant les groupes formés par les personnes. On constitue le nombre de groupes de 2, 3, 4 et 5 désiré.

L'animatrice ou l'animateur demande: «combien de graines as-tu en tout?».

Après le calcul par addition répétée (premier sens de la multiplication), on reprend en demandant de formuler autrement:

2 graines par pot et j'ai 7 pots:2 x 7 =
(j'ai donc 14 graines réparties dans 7 pots, 14 ÷ 7 = )

ou 7 pots de 2 graines: 7 x 2 =

3 graines par pot et j'ai 8 pots:3 x 8 =
(j'ai donc 24 graines réparties dans 8 pots, 24 ÷ 8 = )

Dans chaque cas, on indique la division correspondante.

Les personnes plantent ensuite les graines dans les pots avec le terreau, en mettant un nombre égal de graines (deux ou trois) dans chacun.

Le groupe se répartit en équipes de deux pour calculer le total des plants semés. Chaque groupe indique sa façon de faire.

Deuxième étape

L'animatrice ou l'animateur:

• demande aux participantes et participants de prendre les caissettes à six cases et de planter une seule graine dans chaque case:

[Voir l'image pleine grandeur]

• par équipes de deux, les personnes sont invitées à coller les caissettes et à calculer combien de plants il y a dans:

[Voir l'image pleine grandeur]

On fait la même chose pour 4, 5, ou 6 caissettes. Si l'on veut vraiment avoir la notion d'aire, il faut s'assurer de bien coller les caissettes, ce qui donne un genre de rectangle divisé en carrés.

On revoit ici la multiplication dans son second sens (aire ou surface). Les équipes doivent expliquer leur stratégie de calcul.

Les personnes plantent ensuite les graines dans les caissettes avec le terreau.

On peut aussi, si on veut, calculer en grand groupe, le nombre total de semis en additionnant le total des graines dans les gobelets et les caissettes.

Troisième étape

L'activité complémentaire qui suit vise à travailler la notion de division en utilisant les graines et les gobelets.

L'animatrice ou l'animateur:

• dépose des gobelets sur la table;
• distribue un nombre déterminé de graines ou un nombre déterminé de gobelets à chaque personne et demande de répartir également les graines dans les gobelets.

Les personnes écrivent l'opération réalisée.

[Voir l'image pleine grandeur]

On poursuit ainsi cet exercice avec plusieurs groupes de graines:
18,24,12,9,27, etc.

On demande aux participantes et participants d'expliquer ensuite l'opération réalisée:

• Comment la répartition s'est-elle faite?
• A-t-on compté les graines une par une? (Si oui, comment faire autrement?)
• Combien de groupes ont été faits?
• Combien chaque groupe contient-il?
• En calcul, comment peut-on écrire ce qui a été fait? (Utiliser le tableau)
• Etc.

Reproduire au tableau le travail de quelques personnes pour mieux faire voir le processus effectué et l'équation écrite.

Durée de l'activité: trois heures

Imprimer l'exercice complet

Notes et commentaires

Il est possible de réaliser ces activités avec d'autres objets que les graines (crayons, verres, jetons, etc.) qui feront aussi bien l'affaire à condition qu'ils se comptent et se répartissent bien en groupes définis.

Les participantes et participants ont beaucoup apprécié cette activité en raison de son caractère concret. Ils ont appris tout en travaillant avec la terre pour planter les semences. Par la suite, de semaine en semaine, ils constataient l'évolution et la croissance des semis.

Activité 4 - La plantation au jardin

Objectifs

Développer les notions d'échelle et de proportions.
Préparer le jardin.

Difficultés que pose l'activité

Une fois les semis terminés, il faut préparer le jardin où on les transplantera lorsqu'ils seront à maturité. Pour ce faire, il faut déterminer la grandeur du terrain auquel on a accès et prévoir comment on va placer les semis. C'est le concept d'échelle qui est utilisé afin de reproduire le jardin.

Raisonnements impliqués et apprentissages attendus:

• Estimer des grandeurs et mesurer des espaces.
• Déterminer un facteur de conversion à respecter.
• Reproduire à petite échelle.
• Travailler avec le système métrique.

Activités préalables

• Connaître la multiplication dans son sens d'aire ou de surface.
• Comprendre la notion de répartition, de division.
• Avoir quelques notions du système métrique.
• Pouvoir estimer, mesurer et arrondir.
• Avoir préparé des semis.

Matériel nécessaire

• Accès à un terrain de jardinage (jardin communautaire)
• Des semis (incluant l'indication de l'espace entre les plants)
• Du papier quadrillé (carrés d'un centimètre), ou du papier quadrillé ordinaire où on attribue à chaque carré la valeur d'un centimètre
• Des rubans à mesurer (unités de mesure métrique et anglaise)
• Des calculatrices
• Du papier à volonté

Déroulement: les étapes

Première étape, travail en grand groupe

La mesure du terrain

L'animatrice ou l'animateur:

• propose au groupe de se rendre au jardin afin de prendre les mesures du terrain que l'on va reproduire à petite échelle;
• demande aux personnes du groupe de prendre la longueur et la largeur du terrain avec le ruban à mesurer;
• laisse les participantes et participants prendre les mesures et vérifie les données.

On note sur papier les dimensions réelles. Dans notre cas, les dimensions du terrain sont de 7,63 mètres par 5, 20 mètres.

De retour en atelier, l'animatrice ou l'animateur:

• écrit au tableau les mesures: 7,63 x 5, 20;
• demande de lire les mesures prises sur le terrain (qu'est-ce que ça veut dire?): 7,63 ou 7 mètres et 63 centimètres de longueur (on prend le temps de bien voir qu'il y a 100 centimètres dans un mètre); 5,20 ou 5 mètres et 20 centimètres de largeur.
• demande si on peut arrondir pour faciliter le calcul? 7,63 est arrondi à 7,60; 5,20 reste tel quel.

Deuxième étape, travail en grand groupe

Trouver le facteur de conversion

L'animatrice ou l'animateur:

• distribue à chaque personne une feuille quadrillée;
• demande au groupe comment on peut rapetisser (ou reproduire) ces dimensions sur les feuilles quadrillées;
• laisse les personnes travailler par essais en vue de définir l'échelle désirée.

À cette étape, pour faciliter le travail de définition du facteur de conversion, on convient de retenir 7 m par 5 m.

L'animatrice ou l'animateur propose:

• si la longueur d'un côté d'un carré = 1 mètre;
• combien de carrés en longueur et en largeur faudra-t-il?

Les personnes dessinent sur la feuille le plan avec ce facteur de conversion (rectangle de 7 carrés de long par 5 carrés de large): on constate alors que l'espace est trop petit pour qu'on puisse dessiner le jardin et qu'il faut agrandir.

On reprend ce travail avec d'autres facteurs:

• si la longueur du plus long côté de 2 carrés mis côte-à-côte = 1 mètre, combien faut-il de carrés pour faire la longueur, pour faire la largeur?
• si la longueur du plus long côté de 3 carrés mis côte-à-côte = 1 mètre, combien de carrés faut-il pour faire la longueur, pour faire la largeur?
• si la longueur du plus long côté de 4 carrés mis côte-à-côte = 1 mètre combien de carrés faut-il pour faire la longueur, pour faire la largeur?

Finalement, les personnes retiennent qu'il faut prendre 4 carrés mis côte-à-côte pour couvrir 1 mètre

[Voir l'image pleine grandeur]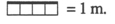

Note: On peut définir une échelle plus grande, ce qui permet de constater que la grandeur de la feuille est une limite à respecter.

Troisième étape, travail individuel

L'animatrice ou l'animateur:

• demande aux personnes de reproduire sur leur feuille quadrillée les dimensions réelles du jardin selon l'échelle fixée, soit

[Voir l'image pleine grandeur]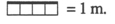

• observe comment les personnes travaillent et les aide au besoin.

On reprend au tableau en formulant:

La longueur du terrain est de 7,60 m (7 mètres et 60 centimètres).

Pour rapetisser les dimensions sur notre feuille, on a défini une échelle de

[Voir l'image pleine grandeur]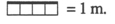

donc, pour la longueur:

4+4+4+4+4+4+4 = 28 (7x4 = 28)
ou
l m + l m + l m + l m + l m + l m + l m = 7 m

Soixante centimètres, qu'est-ce que ça veut dire? Comment peut-on le dessiner sur notre plan?

On doit laisser les personnes l'estimer sur leur plan, discuter de leurs réponses et leur demander d'expliquer leur façon de calculer 60 cm.

Il est conseillé aux animatrices et animateurs de visionner la vidéo La sauce à ... calculer qui leur donnera des idées sur la «gestion de classe» et l'importance de la verbalisation dans les stratégies de calcul des personnes participantes: comment en es-tu arrivé à cette réponse?

Reprendre:

Soixante centimètres, est-ce plus ou moins que la moitié d'un mètre?
Il y a 100 centimètres dans un mètre.
Quelle est la moitié d'un mètre?
Cinquante centimètres, ça représente combien de carrés?

[Voir l'image pleine grandeur]

Donc 60, c'est plus ou moins que 50?
C'est un peu plus que 50.

Sur notre plan, combien de carrés doit-on prendre pour représenter 60 cm?
60 cm = un peu plus que

[Voir l'image pleine grandeur]

Ainsi, la longueur totale à notre échelle représente environ 30 carrés.

On recommence le même exercice pour la largeur: 5,20 m.

On peut calculer la surface et le périmètre du jardin 7,60 de longueur x 5,20 de largeur =

On initiera à la notion d'aire ou de surface à l'aide d'une grande feuille de papier d'un mètre carré. Chaque personne peut s'en fabriquer une à l'aide de papier journal, par exemple, que l'on mesure, découpe et colle pour avoir la bonne dimension. On dispose ensuite la feuille de papier par terre pour voir ce que représentent un, deux, trois, quatre, cinq,... mètres carrés. Certaines personnes voudront comparer avec la verge carrée. On fait alors la même chose et on pose côte à côte le mètre carré et la verge carrée. On peut aussi déposer la verge carrée sur le mètre carré pour voir la différence. Quand les gens ont bien compris le sens et la dimension du mètre carré, on cherchera à l'aide du plan quadrillé l'aire du jardin.

On peut utiliser les unités de blocs à base dix pour découvrir la formule permettant de trouver l'aire. On peut, sinon, utiliser de petits cartons carrés et jouer avec la disposition. C'est un bon moyen de s'exercer aux tables de multiplication.

La meilleure façon de trouver le périmètre est de mesurer en posant une corde tout autour du jardin. Les personnes utilisent le mot «tour» au lieu de périmètre et n'ont, en général, aucune difficulté avec cette notion.

Quatrième étape, travail individuel

L'animatrice ou l'animateur:

• demande à chaque personne de dessiner des rangées où seront transplantés les semis, en respectant un espace nécessaire pour marcher;
• observe de quelle façon les participantes et participants travaillent et les aide au besoin;
• demande aux gens du groupe de dire combien de rangs ont été dessinés au total sur leur plan et quelle est la distance entre chacun;
• laisse les participantes et participants discuter et commenter.

Note: Plusieurs personnes ont dessiné des rangées distancées de quelque 5 cm ou un peu plus.

On reprend ensuite en grand groupe:

• Pour pouvoir marcher dans le jardin, arroser les plants et y travailler, quelle serait la largeur idéale à prévoir entre deux rangs? Les personnes évaluent à l'aide de leur ruban à mesurer. On en arrive à la conclusion qu'il faudrait aménager une distance d'environ 50 cm entre chaque rang, dans la mesure où les plants vont pousser et prendre plus d'espace.

Cinquante centimètres, ça veut dire combien de carrés à notre échelle?

[Voir l'image pleine grandeur]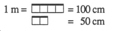

Donc, à tous les 2 carrés, on doit dessiner un rang.

On demande aux gens du groupe de calculer combien il y aura de rangs au total, si on laisse une allée de 50 cm de large entre chaque rang.

Les personnes dessinent les rangs sur leur feuille quadrillée.

Note: Si l'on veut, on peut aussi calculer l'espace requis entre les plants (travail sur la largeur, soit 5,20 m).

Exemple: Entre les plants de tomates, il faut garder un espace de 40 cm; combien de semis peut-on planter? Entre les plants de basilic, il faut garder un espace de 25 cm; combien de semis peut-on planter?

Durée de l'activité: trois heures

Imprimer l'exercice complet

Notes et commentaires

Pour les groupes qui ont choisi de faire le jardin, cette activité mettrait un terme au thème des semences. Elle leur a permis d'approfondir certaines notions mathématiques en pratiquant notamment la multiplication dans ses deux sens (celui d'addition répétée et celui d'aire ou de surface), la division et les échelles et proportions.

Par son caractère concret et la variété des situations d'apprentissage possibles, cette activité s'est avérée très intéressante pour les participantes et participants, qui y ont trouvé des exercices correspondant à leurs niveaux d'avancement respectifs. Ceci constitue un élément important pour les groupes hétérogènes, composés de personnes qui n'ont pas la même expérience mathématique et ne partent donc pas du même niveau.

Activité 5 - La vente des semis

Objectifs

Pratiquer les opérations de base (addition, division, etc.).
Développer la notion de prix de revient.
Travailler avec l'argent et le change.
Préparer la vente des semis.

Difficultés que pose l'activité

Les personnes participantes font souvent des travaux comme la couture, le gardiennage à la maison, etc., qui occasionnent des dépenses (achat de tissus, nourriture pour les enfants ou autres) dont elles doivent tenir compte pour fixer le prix qu'elles demandent pour réaliser ces travaux.

La vente des semis implique que l'on calcule le prix de revient de la production pour arriver à déterminer le prix de vente de chacun des plants. On doit donc additionner, parfois multiplier, pour connaître le prix de revient et le coût total de production, mais on doit aussi répartir ce coût sur le nombre de plants produits pour fixer le prix à l'unité. Il importe alors de reconnaître et d'appliquer le sens des quatre opérations de base.

D'autre part, au moment de la vente des semis, le travail porte davantage sur l'argent, la monnaie et le change. Cette vente amène de plus les participantes et participants à développer leur autonomie et les relations interpersonnelles.

Raisonnements impliqués et apprentissages attendus:

• Comprendre ce qu'est le prix de revient.
• Connaître le sens des quatre opérations de base.
• Comprendre la notion de profit
• Lire une facture.
• Se familiariser avec le monde des affaires et mieux comprendre de quoi est composé le prix des produits que l'on achète.

Activités préalables

• Avoir préparé des semis.
• Avoir travaillé les opérations de base.

Matériel nécessaire

• Des semis
• Des calculatrices
• Les factures du matériel de production (terreau, caissettes, gobelets, semences, etc.)
• Une caisse enregistreuse et un fonds de caisse

Déroulement: les étapes

Première étape, travail en grand groupe

L'animatrice ou l'animateur:

• entame la discussion en demandant aux personnes du groupe de quelle façon on va fixer le prix des semis.

- Les personnes vont donner un prix approximatif, en se basant sur leur propre expérience et sur les prix en vigueur sur le marché. Elles s'entendent sur un montant, par exemple 1,50$.

• demande comment on peut être certain que ce prix est correct, ni trop haut, si on veut les vendre, et ni trop bas.

- Comment le prix pourrait-il être trop bas?
- Qu'est-ce qu'on a dû faire pour commencer les semis ?
- Il a fallu planter les graines dans des contenants, avec de la terre.
- Où a-t-on pris le matériel?
- On l'a acheté.
- Il a fallu payer le matériel que l'on a utilisé pour les semis.
- En vendant les semis 1,50$ chacun, arrivera-t-on à payer notre matériel? Certaines personnes répondent oui, d'autres non.
- Comment faire pour le savoir, pour être sûr de ne pas se tromper?

En calculant ce que le matériel nous a coûté, pour savoir à combien les semis nous reviennent: c'est le prix de revient.

Deuxième étape, en grand groupe

L'animatrice ou l'animateur:

• prend les factures du matériel acheté, en distribue une copie à chaque personne; on observe ce qui est inscrit et on en fait la lecture;
• inscrit le total de chaque produit au tableau (en illustrant les produits au besoin) et invite le groupe à refaire ensemble l'addition.

Les personnes travaillent soit avec leur calculatrice, soit à la main. Exemple de facture:

2 sacs de terreau de 30 litres à 3,50$/sac	7,00 $
1 boîte d'os moulu à 6,89$ le kilo	6,89
4 enveloppes de graines de fleurs à l,29$/enveloppe	5,16
3 enveloppes de graines de fines herbes à l,15$/enveloppe	3,45
2 paquets de 8 petits gobelets à l,75$/paquet	3,5
1 paquet de 20 grands gobelets à 2,19$/paquet	2,19
4 paquets de 10 grands contenants à 3,48$/paquet	13,92
Total:	42,11
Taxe	5,9
	48,01 $

On fait remarquer alors la place du 0 dans l'écriture de la monnaie.

Note: on peut aussi développer davantage l'exercice en travaillant à partir de la facture: les données pertinentes, les fractions, les taxes, la division, la multiplication, etc. Par exemple, on a utilisé un (ou un demi) sac de terreau sur les deux achetés; si une enveloppe de graines coûte 1,15$, combien coûteront deux enveloppes, etc.

Troisième étape

L'animatrice ou l'animateur:

• pose au groupe la question suivante: on sait que le prix total de notre matériel est de 48,01$ et qu'on a préparé 213 semis. Comment peut-on savoir le prix de revient de chaque semis, ce que coûte réellement chaque semis?
• suggère de procéder de la façon suivante: en supposant que chaque semis nous rapporte 1,00$, combien d'argent allons-nous recevoir?
  213 x 1,00$ = 213,00$ (c'est beaucoup plus que 48,01$)

Supposons maintenant que chaque semis rapporte 500, combien d'argent allons-nous recevoir?

La moitié de l'argent que l'on recevrait en les vendant 1,00$.

213$, c'est:
100$ +100$+10$ +1$ + 1$ + 1$

La moitié =
100$ + 5$ + 50¢ + 50¢ + 50¢ = 106,50$

ou
213$ ÷ 2 = 106,50$ (c'est encore beaucoup plus que 48,01$)

On refait le même calcul à 25¢ chaque semis (la moitié de 50¢), ce qui donne 53,25$ (ce qui se rapproche de la somme payée pour notre matériel).

On peut donc estimer que le prix de revient de chaque semis est d'environ 25¢: c'est comme si on séparait (divisait) le total du prix du matériel par le nombre de semis que l'on a faits.

Note: les plus avancés pourront le faire sur leur calculatrice: 48,01$: 213 = 23¢ (arrondi) et 23¢ x 213 = 48,99$

Quatrième étape

Établir le prix de vente et le profit escompté.

L'animatrice ou l'animateur demande:

• 53,25$, est-ce que c'est plus que notre prix de revient, à savoir 48,01$? C'est un peu plus que 48,01$.
• Quelle est la différence? On laisse travailler les participantes et participants (au besoin, utiliser de l'argent en coupures de 20, 10, 5, 2 et de la monnaie).
• 5,24$, c'est quoi au juste? C'est ce qui va nous rester après avoir payé notre matériel, ou c'est la différence entre l'argent que l'on reçoit par la vente de tous les plants et l'argent dépensé pour acheter le matériel.

Quelle opération fait-on pour trouver ce qui reste? Une soustraction. On fait ensemble, au tableau, la soustraction avec emprunt:

[Voir l'image pleine grandeur]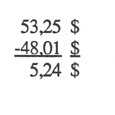

Donc, en vendant chaque semis 25¢, il va nous rester 5,24$ puisqu'il faut enlever 48,01$ du 53,25$ pour payer notre matériel. 5.24$, c'est aussi notre profit.

Les personnes décident ensemble si elles veulent qu'il reste plus d'argent après la vente des semis, si elles désirent que cette vente soit en même temps une activité-bénéfice.

Dans ce cas, on calcule alors par hypothèse. Pour chaque hypothèse, on reprend le calcul (à l'aide de l'argent, de la calculatrice ou au tableau).

On peut aussi former des équipes de deux personnes. Chacune va travailler des hypothèses différentes et donnera les résultats au groupe en expliquant sa démarche.

Si on vend les semis 1,00$, qu'est-ce qui reste, quel sera notre profit? Si on les vend 50¢,30¢, qu'est-ce qui reste, quel sera notre profit?

Cinquième étape

Il faut prévoir à l'avance une période d'annonces ou de publicité de la vente de semis auprès des personnes qui fréquentent le groupe d'alphabétisation, ou à l'extérieur si on le désire.

Avant la vente

L'animatrice ou l'animateur demande aux personnes de se répartir en équipes de travail pour:

• étiqueter les semis: écrire le type de semis et son prix;
• placer les semis sur des tables;
• préparer un fonds de caisse de 10,00$ (billets et monnaie) pour la caisse enregistreuse.

Pendant la vente

Les personnes, par équipes de deux et à tour de rôle, sont responsables de la caisse enregistreuse. L'animatrice ou l'animateur guide le travail.

Les personnes reçoivent l'argent des acheteurs, font marcher la caisse enregistreuse et rendent la monnaie.

Après la vente

L'animatrice ou l'animateur:

• demande aux participantes et participants de calculer le total de l'argent qu'il y a dans la caisse en inscrivant sur un bordereau le nombre de billets de 5$, de 2$ et le détail de la monnaie;
• demande au groupe combien d'argent a été déposé dans la caisse au début, comme fonds de caisse;

A-t-on recueilli cette somme pour notre activité-bénéfice?
On laisse les participantes et participants discuter.
Non, parce qu'il faut payer notre matériel.
On doit donc enlever 48,01$ de cette somme.
On calcule le bénéfice.
On dépose l'argent à la caisse.

Imprimer l'exercice complet

Notes et commentaires

Cette dernière activité permet de pratiquer le calcul de l'argent et du change, de comprendre l'un des sens de la soustraction et la notion de profit (ou de perte). Les personnes l'apprécient parce qu'elles ont la responsabilité de la vente, à tous les niveaux.

Globalement, le thème des semences permet d'explorer plusieurs notions mathématiques. Les exercices qui s'y rattachent favorisent la réalisation d'un cycle d'apprentissage complet où telle activité en amène naturellement une autre, où telle notion est complétée par une nouvelle qui la suit.

En plus des notions purement mathématiques, nous développons d'autres éléments tout aussi importants tels que la confiance en soi, l'autonomie, la capacité de créer, de mener à terme une production concrète en passant par toutes les étapes de sa réalisation.

Annexe

[Voir l'image pleine grandeur]

Annexe 1 – Le matériel utilisé pour le dénombrement [...]

Le matériel utilisé pour le dénombrement et les opérations de base

Pour les activités sur le dénombrement et les opérations de base, il est nécessaire de se procurer de grandes quantités d'objets, au moins quelques centaines de chacun. Il faut cependant faire attention car certains objets se manipulent moins bien que d'autres ou sont bruyants lorsqu'on les manipule. Il faut aussi éviter les objets ronds qui roulent et tombent par terre car cela nuit à la bonne marche de l'activité.

Nous avons travaillé avec:

• des sous noirs;
• des jetons de bingo;
• des bâtonnets de café en plastique;
• des gobelets en plastique utilisés pour la distribution de médicaments;
• des anneaux en bois qu'on utilise pour le jeu de piche ou «pichenolle» (on peut aussi utiliser ces anneaux avec l'abbaque).

Nous avons aussi utilisé:

• des verres à bière en plastique (ils contiennent une petite bière);
• des verres à eau en plastique de 8 onces;
• des élastiques pour attacher les bâtonnets;
• de la ficelle pour attacher les anneaux en bois.

La manipulation de ces objets contribue à l'acquisition de la notion du nombre (on apprend à compter en comptant). Elle favorise aussi le développement du concept de la dizaine et de la centaine. Tous ces objets peuvent être empilés (tes gobelets), regroupés dans un contenant (les sous et les jetons) ou attachés (les bâtonnets) en paquets de 10 puis de 100 pour une meilleure compréhension. Par la suite, on introduira les blocs à base dix qui exigent un premier niveau d'abstraction puisque la dizaine et la centaine sont d'un seul bloc et donc non décomposables.

Les objets qu'on ne peut attacher, sont donc regroupés dans des contenants. Il faut un petit contenant pour illustrer la dizaine et un plus grand pour la centaine. Nous avons utilisé les verres en plastique, des grands et des petits pour travailler sur le dénombrement Nous avons choisi les verres parce qu'ils sont légers et qu'ils se manipulent facilement sans faire de bruit. De plus, ils ne coûtent presque rien, ce qui permet à chaque individu d'avoir son propre matériel.

De plus, comme le regroupement n'est pas déterminé d'avance, on peut le structurer, l'organiser soi-même: on empile facilement dix petits verres dans un grand verre pour illustrer, constituer ou décomposer la centaine.

Par la suite, il est facile de passer au stade semi-concret en dessinant un grand rectangle pour représenter le grand verre de 100 et un petit rectangle pour le petit verre de dix.

D'autres suggestions de matériel:

• les contenants de crème à café qu'on peut récupérer,
• les bâtons de «pop sicle» qu'on peut facilement se procurer dans les épiceries ou centres d'artisanat;
• des feuilles de papier,
• des crayons;
• des trombonnes;
• des pois ou des fèves, etc.

On pourrait aussi utiliser:

• des contenants de yogourt de 250 et 500 ml;
• des sacs en plastique «ZipLoc» petits et grands.

Il faut aussi:

• un carton comme ci-dessous d'environ 20par60 cm. On peut le fabriquer en atelier avec du carton fort (Bristol ou BainBridge), blanc de préférence.

[Voir l'image pleine grandeur]

Pour le thème «Les semences», il faut:

• au minimum 8 à 10 caissettes de semis pour 6 plants;
• des pots de 8 à 10 cm de diamètre, en plastique ou en «carton brun biodégradable» en nombre suffisant pour les semis et les transplantations;
• des graines;
• un ou deux sacs de 10 kg de terre à semence.

Lien vers le contenu vidéo

La sauce à... calculer ou les mathématiques en alphabétisation populaire

Les autres publications du RGPAQ

Les autres publications du RGPAQ dans la série Un visa pour l'alpha pop

SOUCISSE, François,
Animation et alphabétisation: guide pratique,
Montréal, R.G.P.A.Q., 1990, 95 p.

DUPUIS, Michèle,
Les personnes analphabètes et l'apprentissage,
Montréal, R.G.P.A.Q., 1990, 85 p.

LEFEBVRE, Françoise,
Approches et méthodes, un livre dont vous êtes le héros:
Aventure dans le labyrinthe des approches et méthodes en alphabétisation,
Montréal, R.G.P.A.Q.,1990,35 p.

SAUNIER, Michèle,
Comment créer...du matériel pédagogique
Montréal, R.G.P.A.Q., 1990,79 p.

BOUDREAU, Guy,
Le langage intégré,
Montréal, R.G.P.A.Q., 1992,71 p.

MIDY, Franklin,
L'évaluation des apprentissages en alpha populaire,
Montréal, R.G.P.A.Q./Service aux collectivités de l'UQAM, 1992,120 p.

JANVIER, Claude et VANASSE, André,
La sauce à... calculer ou les mathématiques en alphabétisation populaire,
Montréal, Les Productions Bonsaï pour le R.G.RA.Q. Et le Service aux collectivités de l'UQAM, 1993, VIDÉO d'une durée de 28'30".

MATHIEU, Réjean,
Agir ensemble démocratiquement,
Montréal, R.G.P.A.Q./Service aux collectivités de l'UQAM, 1993,112 p.

Crédits

Coordination
Marie-Hélène Deshaies, Berthe Lacharité, Liliane Rajaonina, Ginette Richard

Rédaction
Francine Loignon, Linda Maziade ainsi que Françoise Lefebvre (pour le chapitre cinq), sous la direction de Claude Janvier

Collaboration à la rédaction
Diane Lambert, Lucie St-Germain

Élaboration et expérimentation des activités
Claudette Bérubé, Françoise Bouchard, Réjane Déry-Bouchard, Martine Dompierre, Diane Guérette, Francine Loignon, Donald Lurette, Claudette Roussel, Martine Soulié, sous la direction de Claude Janvier

Comité de pédagogie
Richard Latendresse, Lucie Latraverse, Colette Paquet

Saisie des corrections
Solange Roy

Révision
Claudine Vivier

Relecture du texte
Claude Janvier, Lucie Latraverse, Françoise Lefebvre, Carmélita Nascimento, Colette Paquet, Hélène Patenaude, Lucie St-Germain

Graphisme
Pierre Lachance

Photographies
Tirées de la vidéo La sauce à... calculer réalisée par André Vanasse des Productions Bonsaï

Correction d'épreuves
Marie-Hélène Deshaies, Nicole Lachapelle, Berthe Lacharité, Liliane Rajaonina

Impression
Service de reprographie, Université du Québec à Montréal

Les opinions exprimées dans ce document sont celles des auteurs et ne représentent pas nécessairement la position officielle du RGPAQ.

Publié par le Regroupement des groupes populaires en alphabétisation du Québec (RGPAQ).

Nous remercions le Service aux collectivités de l'UQAM pour son soutien professionnel et financier. Le Secrétariat national à l'alphabétisation a contribué au financement du programme de perfectionnement.

On commande des exemplaires du document en s'adressant au:

Regroupement des groupes populaires en alphabétisation du Québec
5040, boulevard St-Laurent, app. 1
Montréal (Québec) H2T 1R7
Téléphone: (514)277-9976
Télécopieur: (514)277-2044